the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Application of a physically based model to forecast shallow landslides at a regional scale
Teresa Salvatici
Veronica Tofani
Guglielmo Rossi
Michele D'Ambrosio
Carlo Tacconi Stefanelli
Elena Benedetta Masi
Ascanio Rosi
Veronica Pazzi
Pietro Vannocci
Miriana Petrolo
Filippo Catani
Sara Ratto
Hervè Stevenin
Nicola Casagli
In this work, we apply a physically based model, namely the HIRESSS (HIgh REsolution Slope Stability Simulator) model, to forecast the occurrence of shallow landslides at the regional scale. HIRESSS is a physically based distributed slope stability simulator for analyzing shallow landslide triggering conditions during a rainfall event. The modeling software is made up of two parts: hydrological and geotechnical. The hydrological model is based on an analytical solution from an approximated form of the Richards equation, while the geotechnical stability model is based on an infinite slope model that takes the unsaturated soil condition into account. The test area is a portion of the Aosta Valley region, located in the northwest of the Alpine mountain chain. The geomorphology of the region is characterized by steep slopes with elevations ranging from 400 m a.s.l. on the Dora Baltea River's floodplain to 4810 m a.s.l. at Mont Blanc. In the study area, the mean annual precipitation is about 800–900 mm. These features make the territory very prone to landslides, mainly shallow rapid landslides and rockfalls. In order to apply the model and to increase its reliability, an in-depth study of the geotechnical and hydrological properties of hillslopes controlling shallow landslide formation was conducted. In particular, two campaigns of on site measurements and laboratory experiments were performed using 12 survey points. The data collected contributed to the generation of an input map of parameters for the HIRESSS model. In order to consider the effect of vegetation on slope stability, the soil reinforcement due to the presence of roots was also taken into account; this was done based on vegetation maps and literature values of root cohesion. The model was applied using back analysis for two past events that affected the Aosta Valley region between 2008 and 2009, triggering several fast shallow landslides. The validation of the results, carried out using a database of past landslides, provided good results and a good prediction accuracy for the HIRESSS model from both a temporal and spatial point of view.
Landslide prediction at a regional scale can be performed following two approaches: (a) using rainfall thresholds based on the statistical analysis of rainfall and landslides, and (b) using physically based deterministic models. While the first approach is currently extensively used at regional scales (Aleotti, 2004; Cannon et al., 2011; Martelloni et al., 2012; Rosi et al., 2012; Lagomarsino et al., 2013), the latter is more frequently applied at slope or catchment scales (Dietrich and Montgomery, 1998; Pack et al., 2001; Baum et al., 2002, 2010; Lu and Godt, 2008; Simoni et al., 2008; Ren et al., 2010; Arnone et al., 2011; Salciarini et al., 2012, 2017; Park et al., 2013; Rossi et al., 2013). The poor knowledge of hydrological and geotechnical parameters' spatial distributions, caused by the extreme heterogeneity and inherent variability of soil at large scales (Mercogliano et al., 2013; Tofani et al., 2017), means that the application of physically based models is generally avoided at regional scales. Conversely, physically based models allow for the spatial and temporal prediction of the occurrence of landslides with high accuracy, producing accurate hazard maps that can be of help for landslide risk assessment and management.
In this work, we apply the physically based HIRESSS (HIgh REsolution Slope Stability Simulator) model (Rossi et al., 2013) in the eastern section of the Aosta Valley region (Italy), in the northwest Alpine mountain chain, in order to test the capacity of the model to forecast the occurrence of shallow landslides at the regional scale. In particular, the objectives of this study are as follows: (i) to properly characterize the geotechnical and hydrological parameters of the soil to feed the HIRESSS model, and to spatialize this punctual information in order to have spatially continuous maps of the model input data; and (ii) to test the HIRESSS code for two selected rainfall events, which triggered several shallow landslides, and to validate the model results. HIRESSS is a physically based distributed slope stability simulator for analyzing shallow landslide triggering conditions in real time and over large areas using parallel computational techniques. In the area selected, an in-depth study of the geotechnical and hydrological properties of hillslopes controlling shallow landslides formation was conducted; this involved performing two campaigns (using 12 survey points) of in situ measurements and laboratory tests. Furthermore, the HIRESSS model was modified to take the effect of the root reinforcement to the stability of slopes based on plant species distribution and literature values of root cohesion into account.
The study area, called “alert zone B” by the regional civil protection authorities, is located in the eastern part of the Aosta Valley region, in the northwest Alpine mountain chain (Fig. 1). The area is characterized by three main valleys: Champorcher Valley, Gressoney or Lys Valley, and Ayas Valley. The first is located on the right side of the Dora Baltea catchment, and represents the southern part of the study area. The second and third valleys show a north–south orientation, and are delimited to the north by Monte Rosa Massif (4527 m a.s.l.) and to south by the Dora Baltea River.
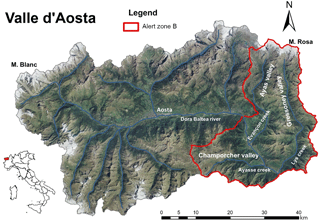
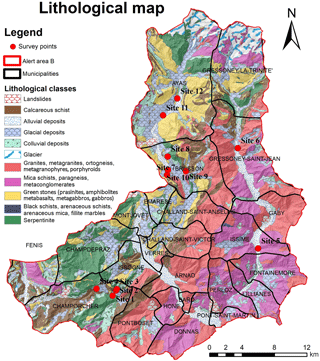
Figure 1The Aosta Valley region in northwest Italy. The study area, alert zone B, is delineated in red.
From a geological point of view, the Aosta Valley is located northwest of the Insubric Line; in particular, there are three systems of Europa chain: the Austroalpine, the Penninic and the Helvetic systems (De Giusti, 2004). Figure 2 shows the lithological map of the study area obtained by reclassifying the geological units according to 11 lithological groups: landslides, calcareous schist, alluvial deposits, glacial deposits, colluvial deposits, glacier, granites, mica schists, green stone, black schists, and serpentinites. The main lithologies outcropping in the study area are metamorphic and intrusive rocks, in particular granites, metagranites, schists, and serpentinite.
The geomorphology of the region is characterized by steep slopes and valleys shaped by glaciers. The glacial modeling is shown in the U-shape of the Lys and Ayas valleys, and the erosive depositional forms found in the Ayas Valley. The three valleys' watercourses, the Lys Creek, the Evançon Creek, and the Dora Baltea River, contributed to the glacial deposits modeling with the formation of alluvial fans. The climate of the region is characterized by high variability that is strongly influenced by altitude (ranging from 400 m a.s.l. of Dora Baltea River's floodplain to 4810 m a.s.l. of Mont Blanc), with a continental climate in the valley floors and an Alpine climate at high altitudes.
The slope steepness and the mean annual precipitation of 800–900 mm are the main landslide triggering factors. These features lead the study area to be prone to landsliding, in particular rockfalls, deep seated gravitational slope deformations (DSGSD), rocks avalanches, debris avalanches, debris flows, and debris slides (Catasto dei Dissesti Regionale – form Val d'Aosta Regional Authorities). In this work we model the triggering conditions of shallow landslides, i.e., soil slips and translational slides, and we do not take other types of movement into account.
The HIRESSS model simulated two past events, one in 2008 and one in 2009, and a validation of the model performance was then carried out comparing the results with the landslide regional database.
The two simulated events are as follows:
-
24–31 May 2008: on 28 and 29 May 2008 intense and persistent rainfall was recorded across the Aosta Valley region with a total precipitation in the study area of about 250 mm causing flooding, debris flows, and rockfalls.
-
25–28 April 2009: from 26 to 28 April 2009 heavy rainfall affected the southeastern part of the Aosta Valley region, with the highest precipitation of about 268 mm recorded at the Lillianes Granges station. This precipitation triggered several landslides.
3.1 HIRESSS description
The physically based distributed slope stability simulator HIRESSS (Rossi et al., 2013) is a model developed to analyze shallow landslide triggering conditions on a large scale at high spatial and temporal resolutions using a parallel calculation method. The model is composed of a hydrological and a geotechnical component (Rossi et al., 2013). The hydrological component is based on dynamic input of the rainfall data, which are used to calculate the pressure head and provide it to the geotechnical stability model. The hydrological model is initiated as a modeled form of hydraulic diffusivity using an analytical solution, which is an approximated form of the Richards equation under the wet condition (Richards, 1931). The equation solution allows us to calculate the pressure head variation (h), depending on time (t) and the depth of the soil (Z). The solutions are obtained by imposing some boundary conditions as described by Rossi et al. (2013).
The geotechnical stability model is based on an infinite slope stability model. The model considers the effect of matric suction in unsaturated soils, taking the increase in strength and cohesion into account. The stability of the slope at different depths (Z values) is computed, as the hydrological model calculates the pressure head at different depths. The variation of soil mass caused by water infiltration on partially saturated soil is also modeled. The original FS (factor of safety) equations (Rossi et al., 2013) were modified taking the effect of root reinforcement (cr) as an increase of soil cohesion (c′) into account as follows:
Regarding the geotechnical influence of roots on the soil strength, roots seem to affect the cohesion parameter only, while the friction angle is poorly or not at all impacted by reinforcement (Waldron and Dakessian, 1981; Gray and Ohashi, 1983; Operstein and Frydaman, 2000; Giadrossich et al., 2010). Therefore, it is necessary to consider the root cohesion when calculating the FS and consequently when applying the HIRESSS model.
The root reinforcement (or root cohesion) can be considered equal to (Eq. 2):
where Tr is the root failure strength (tensile, frictional, or compressive) of roots per unit area of soil, Ar∕A is the root area ratio (proportion of area occupied by roots per unit area of soil), k is a coefficient dependent on the effective soil friction angle and the orientation of roots. The measure of cr varies with vegetal species; within a single species the measure depends on how plants respond to environmental characteristics and fluctuations.
Therefore, the new equation for FS at unsaturated conditions is as follows:
where ϕ is the friction angle, α is the slope angle, γd is the dry soil unit weight, y is the depth, γw is the water unit weight, h is the pressure head, hb is the bubbling pressure, and λ is the pore size index distribution. In saturated condition the equation for FS (Rossi et al., 2013) becomes
where γsat is the saturated soil unit weight.
One of the major problems, associated with the deterministic approach employed on a large scale, is the uncertainty of the static input parameters or geotechnical parameters of the soil. The method used for the estimation of parameters' spatial variability is the Monte Carlo simulation. The Monte Carlo simulation achieves a probability distribution of input parameters, providing results in terms of slope failure probability (Rossi et al., 2013). The developed software uses the computational power offered by multicore and multiprocessor hardware, from modern workstations to supercomputing facilities (HPC), to achieve the simulation in a reasonable runtime and is compatible with civil protection real-time monitoring (Rossi et al., 2013). The HIRESSS model loads spatially distributed data arranged as 12 input raster maps and the maps of rainfall intensity. These input raster maps are slope gradient, effective cohesion (c′), root cohesion (cr), friction angle (ϕ′), dry unit weight (γd), soil thickness, hydraulic conductivity (ks), initial soil saturation (S), pore size index (λ), bubbling pressure (hb), effective porosity (n), residual water content (qr), and rainfall intensity.
3.2 HIRESSS input data preparation
The input parameters can be divided in two classes: the static data and the dynamical data. Static data are geotechnical and morphological parameters while dynamical data are represented by the hourly rainfall intensity. Static data are read only once at the beginning of the simulation while dynamical inputs are continuously updated.
The HIRESSS input is in raster, which means that point data and parameters have to be adequately spatially distributed. In this application the spatial resolution was 10 m.
Static data
The slope gradient was calculated from the DEM (digital elevation model). The DEM has a resolution of 10 m and is dated 2006. Effective cohesion, friction angle, hydraulic conductivity, effective porosity, and dry unit weight were obtained and spatialized according to lithology. The soil punctual parameters were derived from the in situ and laboratory geotechnical tests and analysis.
In particular, the properties of slope deposits were determined by in situ and laboratory measurements (Bicocchi et al., 2016; Tofani et al., 2017) at 12 survey points. To carry out the in situ tests the survey points were selected using the following characteristics: (i) physiography, (ii) landslides occurrence, and (iii) geolithology (Fig. 2). Regarding the first point, a high-resolution DEM (from Val d'Aosta Regional Authorities) and careful first surveys were used to identify the most suitable slopes. The surveys took place in two sessions, the first in August 2016, and the second in September 2016. The following analyses were conducted:
-
Registration of the geographical position was undertaken using a GPS and photographic documentation of the site characteristics (morphology and vegetation).
-
The in situ measurement of the saturated hydraulic conductivity (ks) was carried out by means of the constant head well permeameter method using an Amoozemeter.
-
Sampling of an aliquot (∼ 2 kg each) of the material was conducted for laboratory tests, including grain size distributions, index properties, Atterberg limits, and direct shear tests.
The permeability in situ measurements and the soil samplings were made at depths ranging from 0.4 to 0.6 m below the ground level. The evaluation of the ks (saturated hydraulic conductivity or permeability) was made with an Amoozemeter permeameter (Amoozegar, 1989). The measurement was obtained by observing the amount of water required to maintain a constant volume of water in the hole. In situ measurements were then entered into the Glover solution (Amoozegar, 1989), which calculated the saturated permeability of the soils. The ks is a very useful parameter not only for slope stability modeling but also for many other hydrological problems (groundwater, surface water and sub-surface runoff, and flow calculation of water courses).
In addition, the samples collected in situ were examined in the laboratory to define a wide range of parameters to more extensively characterize the deposits. In particular, the following tests were performed in order to classify the analyzed soils:
-
grain size distribution (determination of granulometric curve for sieving and settling following ASTM recommendations), and classification of soils (according to AGI and USCS classification, Wagner, 1957);
-
determination of the main index properties (porosity, relationships of phases, natural water content (wn), the respective natural and dry unit weight (γ) and (γd)) following the ASTM recommendations;
-
determination of Atterberg limits (liquid limit (LL), plastic limit (PL), and plasticity index (PI));
-
direct shear test on selected samples.
Soil thickness was calculated by the GIST model (Catani et al., 2010; Del Soldato et al., 2016). Soil characteristic curves parameters (pore size index, bubbling pressure, and residual water content) were derived from literature values (Rawls et al., 1982).
Root cohesion variations in the area (at the soil depth chosen for the physical modeling with HIRESSS) were first obtained, identifying the plant species and determining their distribution from in situ observations and vegetational maps (Carta delle serie di vegetazione d'Italia, Italian Ministry of the Environment and Protection of Land and Sea). Then, the measure of cohesion due to the presence of roots was assigned to each subarea according to the dominant plant species and literature root cohesion value for that species (Bischetti, 2009; Burylo et al., 2010; Vergani et al., 2013, 2017), which were calculated considering the fiber bundle model (Pollen et al., 2004). The measure of cr varies with vegetal species; within a single species the value depends on how plants respond to environmental characteristics and fluctuations. Therefore, a map of root cohesion variations, obtained as previously mentioned, is a simplification of reality. This is a necessary simplification as the known methods to evaluate root cohesion variations are not suitable for wide areas and acceptable measurement times.
The last static input data, in this study, are the exposure rock mask. These data were defined considering the lithological and land use maps, so that the HIRESSS model avoided simulation on steep slopes made of bare rocks.
The geotechnical properties and root cohesion of the soils have been spatialized with respect to a lithological classification.
For each lithological class and plant species the mean value has been selected in order to obtain the HIRESSS input raster parameters.
Dynamic data
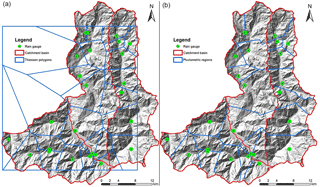
In the study area, the rainfall hourly data from 27 pluviometers were available; therefore, it was necessary to spatially distribute them to generate a 10 × 10 m cell size input raster to ensure correct program operation. The rainfall data were elaborated by applying the Thiessen polygon methodology (Rhynsburger, 1973), modified to take the elevation into account. Thiessen polygon methodology allows us to divide a planar space into regions, and to assign the regions to the nearest point feature. This approach defines an area around a point, where every location is nearer to this point than to all the others. Thiessen polygon methodology does not consider the morphology of the area; therefore, alert zone B was divided in three catchment areas and the polygons were calculated for each of the rain gauges considering the reference catchment basin (Fig. 3).
4.1 HIRESSS input data
The results of the geotechnical and hydrological characterization of the soils of the 12 survey points are shown in Table 1 for all survey sites.
Table 1Geotechnical properties of survey points (grain size distribution, Atterberg limits, index properties, permeability, and shear strength parameters).
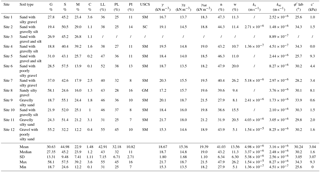
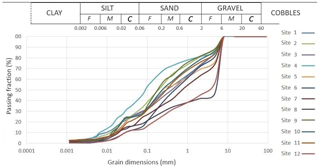
The results of granulometric tests show that the analyzed soils are predominantly sands with silty gravel (Fig. 4 and Table 1). Regarding the index properties, the natural soil water content values were predominantly about 20 % by weight, with maximum and minimum values of 5.1 and 26.2 %, respectively. These values reflect their different ability to hold water in their voids. The measured natural unit weight (γ) varied between 15.3 and 21.7 kN m−3, depending not only on the different grain size distribution but also on the different thickening and consolidation states. In addition, the measured values for the saturated unit weight (γsat) ranged between 18.2 and 21.5 kN m−3 (Table 1).
The Atterberg limits (LL and PL) were measured on samples with a sufficient passing fraction (> 30 % by weight) through a 40 ASTM (0.425 mm) sieve. For prevalently sandy samples, LL values were mostly around 40 % of water content (% by weight), while the PL was around 30 % (Table 1).
The effective friction angle varied between a minimum of 25.6 and a maximum of 34.3∘, while the effective cohesion ranged from a minimum of 0.0 to a maximum of 9.3 kPa. Consistent with the presence of sandy soils, the saturated permeability values were around a medium-high value of 10−6 m s−1. The minimum and maximum values were found between 1.36 ⋅ 10−7 and 1.54 ⋅ 10−5 m s−1. Considering the poor variability of samples, the permeability values were relatively homogeneous and in accordance with the values reported in the literature (Table 1).
The additional cohesion induced by roots assumes different values not only depending on plant species and environmental characteristics but also on depth of soil, as roots' diameter and density vary with latter. Because of such evidence, studies on root cohesion in different species report values as a function of soil depth. In this study region, soils were thinner than in areas where previous studies have been carried out. In such thin soils, root systems organize their growth depending on available space and do not reach the same depth as roots in thick soils. Consequently, in this context root cohesion of species at different depths was dissimilar to the literature values. Considering this, the map regarding the variation of root cohesion was processed taking the minimum cohesion value for each species (among those specified for each species at the different depth) reported in literature. By doing this, the contribution of vegetation to the stability of slopes is considered in the FS calculation, whilst an overestimate of root cohesion is avoided.
In the study area, root cohesion, defined as mentioned above, ranged from a minimum of 0.0 kPa (mainly in the outcrop area) to a maximum of 8.9 kPa (in areas occupied by mountain maple on the left bank of Dora Baltea River).
In Table 2, the mean values of each of the input parameters are reported with respect to lithological class.
Table 2Spatialized geotechnical parameters of each lithological class as input for the HIRESSS model.
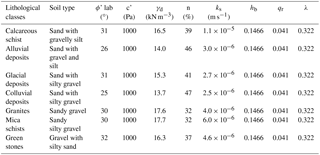
The pore size index, bubbling pressure, and residual water content were constant in the study area, measuring 0.322 (−), 0.1466 m, and 0.041 (−), respectively.
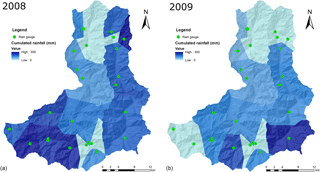
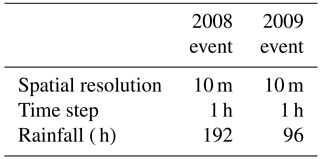
The distributed soil parameter maps are shown in Fig. 5. The results of rainfall data, elaborated using Thiessen polygon methodology, are 192 and 96 rainfall hourly maps for the 2008 and 2009 events, respectively. In Fig. 6 the cumulative maps of each event are shown.
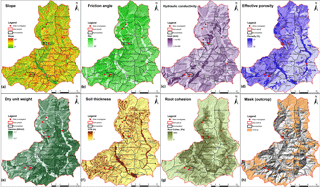
Figure 5Static input parameters for HIRESSS model: (a) slope gradient, (b) friction angle, (c) hydraulic conductivity, (d) effective porosity, (e) dry unit weight, (f) soil thickness, (g) root cohesion, and (h) exposure rock mask.
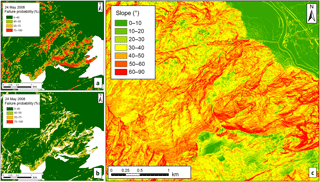
Figure 7Example of the numerical mask used to remove the false positives for the first event simulated (24–31 May 2008). (a) The HIRESSS result for the first day of simulation with false positive pixels. (b) The probability map after the numerical mask implementation. (c) The slope map, which shows that the pixels with high probability of landslide occurrence are located where the slope is higher than 60 %.
4.2 HIRESSS simulation
The HIRESSS model was used to simulate two past events; one in 2008 (24–31 May) and one in 2009 (25–28 April), both of which triggered several landslides in the study area.
The HIRESSS input data were entered into the HIRESSS model to obtain day-by-day maps of the landslide occurrence probability. The main characteristics of the simulation are shown in Table 3.
The results of the simulations for both events on the first day of the simulation showed pixels with a high landslide probability occurrence in absence of rainfall. These pixels were false positives (i.e., pixels identified unstable by the model but were not really unstable) and occurred due to morphometric reasons, predominantly high slope angles. To remove these false positives, a numeric mask was applied. Using GIS software commands, it was possible to calculate the number of pixels on the first simulation day with a trigger probability value greater than 80 % and delete them (Fig. 7). The mask was then applied to the rest of landslide occurrence probability maps. The resulting maps for each days of the simulated events are shown in the Figs. 8 and 9.
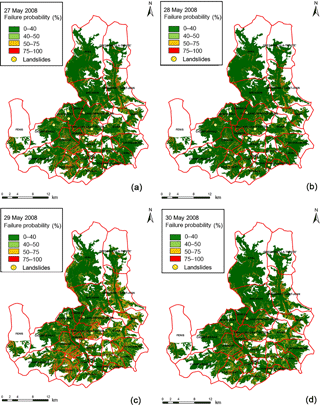
Figure 8HIRESSS landslide probability maps of the simulated event from 24 to 31 May 2008 and the reported landslides during this event, with on the four critical days: (a) 27 May 2008, (b) 28 May 2008, (c) 29 May 2008, and (d) 30 May 2008.
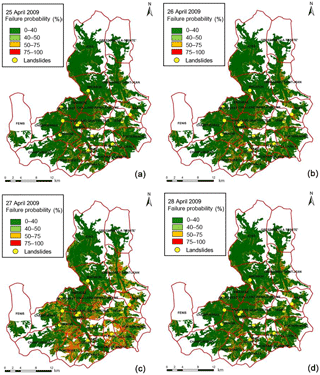
Figure 9HIRESSS landslide probability maps of the simulated event between 25 and 28 April 2009 and the reported landslides during this event, (a) 25 April 2009, (b) 26 April 2009, (c) 27 April 2009, and (d) 28 April 2009.
The results of the first simulated event (24–31 May 2008) are shown in Fig. 8. The failure probability in the whole area was negligible for the first four days (from 24 to 27 May 2008) (Fig. 8a). The rainfall intensity then increased from 27 May and reached its highest value on 29 May, when the precipitation value was around 100 mm in the eastern sector of study area. The HIRESSS model simulate this passage well, with the 28 and 29 May 2008 landslide occurrence probability maps showing a considerable increase in the probability of failure with maximum values around 90 % in the east of alert zone B (Fig. 8b, c). In the following days rainfall intensity decreases, and the probability also slowly decreases, although it is still high on 30 May 2008.
Concerning the second event (25–28 April 2009), the landslide occurrence probability was negligible for the first two days (25 and 26 April 2009) over the whole area (Fig. 9a, b), due to the low rainfall intensity. From 27 April 2009 rainfall became more intense, especially in the southeast sector of the region where the cumulated rainfall average was about 151 mm. The probability maps show high values during these days (Fig. 9c, d). This event led to many landslides being triggered (as reported in the database).
In order to validate the HIRESSS simulations the database of landslides triggered during the two events were compared with the models results.
In general, for both events temporal validation showed that the daily highest probability of occurrence, computed by HIRESSS, correspond with days with landslide occurrences and the most intense precipitation.
For the first simulated event, landslides reported in the database are dated 30 and 31 May 2008 (Fig. 8d) which correspond to the days with highest probability of occurrence. The same can be seen for the second event, with many landslides being triggered between 27 and 28 April 2009 (as reported in the database).
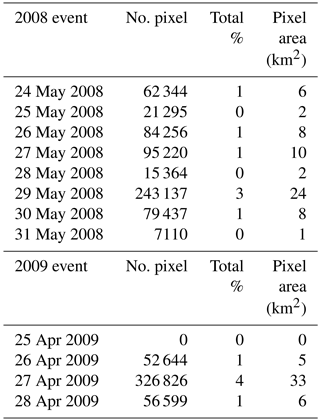
In Table 4 the results with over a 75 % slope failure probability for both events are highlighted and confirm the correct temporal occurrence of landslides. In particular, we notice that for the first event (2008) the number of unstable pixels (failure probability > 75 %) increases from 29 May with a total extension of the unstable area of about 24 km2. For the 2009 event, the number of unstable pixels increases from 27 April with an extension of 33 km2.
Temporal validation was also carried out, considering daily cumulative rainfall compared to the landslide failure probability. In particular, a median of the landslide occurrence probability was calculated for four pluviometric areas identified by Thiessen polygons methodology, modified according to limits of river basins; this was undertaken both for the event in May 2008 and for the event in April 2009 (Fig. 10a, b). As could be expected, the results showed that when the highest rainfall intensity was measured, the highest probability of occurrence was computed for all areas and for both events.
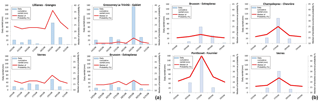
Figure 10Correlation graphs between the daily cumulative rainfall and the median of the landslide occurrence probability for both events.
Spatial validation was performed following a pixel-by-pixel method, which is the most complex method and consists of comparing the probability of the instability of each pixel with the pixels involved in the actual event. This validation implies a great deal of uncertainty in the results, since the reports of landslide events may have errors regarding the precise spatial location and the size of the phenomenon. To overcome this problem and to take probable errors caused by the actual spatial location in the database into account, an area of 1 km2 (called the influence area) around the point of the landslide was considered in the validation analysis. Inside the influence area, pixels that had a 75 % probability of failure were considered unstable.
Figure 11 shows an example of a landslide event that occurred in the Arnad municipality on 30 May 2008. The model computes a low failure probability on 24 May 2008 and an increase in the failure probability on 30 May 2008. In Fig. 11a and b it is possible to note that, inside the red circle, the red and yellow areas have increased on 30 May with respect to 24 May. In this case, the model was able to correctly identify such movement. To better highlight this validation, Fig. 11c shows the number of pixels above 75 % probability that were calculated by the model within a ca. 1 km2 circular area around all the landslides that occurred during 2008 event. For some of the reported landslide events, the number of pixels above 75 % increases on 30 May 2008; however, in the cases of the Champdepraz and Montjovet 2 events the probability does not increase. This may have been caused by the low precision regarding the location of the reported landslide, and because some of the real landslides reported are other types of movements (rockfalls, rotational slides) that cannot simulated by the HIRESSS model.
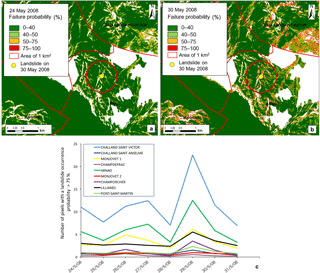
Figure 11An example of a landslide event that occurred in the Arnad municipality compared to a landslide occurrence probability map, (a) before and (b) after a rainfall event. (c) The number of pixels above 75 % failure probability calculated by the model for all the landslides triggered during the event in the study area.
Table 4HIRESSS results for both the 2008 and 2009 events. “No. pixel” represents the number of pixels with a slope failure probability over 75 %; “Total %” represents the percentage of pixels with slope failure probability over 75 %; and “Pixel area (km2)” represents the extension of the area with slope failure probability over 75 %.
The application of the HIRESSS model to a portion of the Aosta Valley region provided good results in terms of the spatial and temporal accuracy of the model as highlighted in Sect. 4.2. The advantage of the regional physically based model, with respect to rainfall thresholds, is that it is possible to predict the occurrence of shallow landslides with metric spatial resolution and hourly temporal resolution.
Conversely, the application of the HIRESSS model has highlighted some important drawbacks, mainly related to (i) the validation of the models results and (ii) the uncertainty of the input parameters.
Validation of the model results
To perform a solid validation it is necessary to have information regarding the spatial location and temporal occurrence of landslides. In particular, the time of occurrence is very rarely known with hourly precision; this is due to the fact that landslides are usually related to a rainstorm, without any other precise information on time of occurrence (Rossi et al., 2013). Concerning the spatial landslides locations, in many cases they are only included in the database as points without any information on the area involved. In our database, provided by the local authorities, landslides are points with information on the day of occurrence.
In synthesis the main problems encountered during the model validation are as follows:
-
The incompleteness of landslide datasets. In general event-based databases are incomplete due to a lack of reporting in mountainous, scarcely populated areas, while most of reported landslides involve infrastructure or water streams (Mercogliano et al., 2013, Tofani et al., 2017). In our case we have two datasets for the two simulated events (2008 and 2009) with 9 and 11 landslides, respectively. The number of reported landslides is very low and not suitable to perform a correct validation for the whole area. In fact, in both events there are some areas that show a high failure probability even though there are no landslides reported. For example, for the 2008 event (Fig. 8), the municipalities of Gressoney Saint Jean and Gaby in the northeast portion of the study area and the municipalities of Pontboset and Issogne in the southern part of the study area show high failure probabilities (> 75 %) but no reported landslides. The same occurs for the 2009 event (Fig. 9) when Gressoney Saint Jean and Pontboset as well as Lillianes and Fontainemore in the southeast portion of the study area show high failure probabilities but no recorded landslides. In these cases, we are not able to discriminate if the model has overestimated the landslide occurrence or it has correctly predicted landslide occurrence since we are not certain about the completeness of the database.
-
Correct spatial location. In our validation landslide dataset the accuracy of the spatial location was very low and the landslides were reported as points (yellow dots in Figs. 8 and 9). Furthermore, we did not know for certain if these points correspond to the triggering area (which would constitute the desirable situation), to the deposition area, or to the position of the elements at risk (house, road, river) from the landslides. For this reason, when performing the spatial validation, we considered an area of 1 km2 around the point in order to take the error in the spatial location of the landslides into account (Fig. 11). In these cases, where the position of the landslides were uncertain, an alternative solution could be to perform a validation aggregating the results using different spatial units, such as first or second order basins as proposed in Rossi et al. (2013). Whilst spatial aggregation overcomes the problem of establishing the correct location of landslides for validation, it causes the high spatial resolution of the HIRESSS model to be lost, which is one of the major benefits of the analysis . The ideal situation would be to have a landslide database realized with the same resolution as the HIRESSS model.
-
Temporal occurrence. The event landslide database provides information concerning the day of the landslide occurrence. The HIRESSS model has a higher temporal resolution, as it is able to provide hourly failure probability maps (Table 3). In order to make a temporal validation, model outcomes have been temporally aggregated in daily maps (Figs. 8 and 9). The results of the temporal validation are quite satisfactory, although due the insufficient information of the landslide database we are unable to make a real validation of the model performance on hourly basis. Also, in this case, a satisfactory analysis of the model performance could only have been carried out if information on the exact time of failure was available.
Uncertainty of the input parameters
Another important limitation related to the application and accuracy of the physically based model is the availability of detailed databases of the physical and mechanical properties of soils in the study areas. The performance of a model can be strongly influenced by the errors or uncertainties in such input data (Segoni et al., 2009; Jiang et al., 2013). Furthermore, the punctual information regarding soil properties has to be spatialized and, in general, is characterized by high spatial variability. The measurement of these parameters is also difficult, time-consuming and expensive, especially when working on large, geologically complex areas (Carrara et al., 2008; Baroni et al., 2010; Park et al., 2013; Bicocchi et al., 2016; Tofani et al., 2017).
In order to prepare raster maps of the input data and feed the physically based models, we adopted a set of constant values for the parameters for distinct lithological units; these values were derived from direct measurements. In particular, we measured soils parameters at 12 survey points (Table 1, Fig. 2) and then spatialized the punctual data according to different lithologies (Table 2). Within the HIRESSS model the soil parameters were then treated with the Monte Carlo simulation, using a equiprobable distribution for each of them.
The HIRESSS model, fed with these parameters provided good results (Sect. 4.2), although the limitations of the validation process are described above.
Nevertheless, further analysis needs to be carried out in the study area in order to define the impact of the uncertainties of the input parameters on model results and to set up the correct approach to increase the efficiency of the model. In particular the following should be considered:
-
Increase the number of survey points in order to a obtain a sufficient number of points for each lithology.
-
Use the normal Gaussian frequency model instead of the equiprobable model in the Monte Carlo simulation for some soil parameters. The normal distribution model, when applicable, obtains more accurate results than using an equiprobable distribution model. This is due to the fact that given a mean value and a standard deviation obtained from the analysis of normally distributed samples, extremely low or high values are associated with low probability of occurrence; therefore, the simulation time is dramatically reduced (Bicocchi et al., 2016, Tofani et al., 2017).
-
To test another approach to spatialize the soil parameters based, for example, on the soil parameter values as random variables using a probabilistic or stochastic approach as proposed by Fanelli et al. (2016) and Salciarini et al. (2017).
The HIRESSS code (a physically based distributed slope stability simulator for analyzing shallow landslide triggering conditions in real time and over large areas) was applied to the eastern sector of the Aosta Valley region in order to test its capability to forecast shallow landslides at the regional scale. The model was applied in back analysis to two past rainfall events that triggered several shallow landslides in the study areas between 2008 and 2009. In order to run the model and to increase its reliability, an in-depth study of the geotechnical and hydrological properties of hillslopes controlling shallow landslides formation was conducted. In particular, two campaigns of on site measurements and laboratory experiments were performed at 12 survey points. The data collected contributed to the generation of an input map of parameters for the HIRESSS model according to lithological classes. The effect of vegetation on slope stability in terms of root reinforcement was also taken into account, based on the plant species distribution and literature values of root cohesion, to product a map of root reinforcement of the study area. The outcomes of the model are daily failure probability maps with a spatial resolution of 10 m. To evaluate the model performance both temporal and spatial validation were carried out. In general, for both the simulated events, the computed highest daily probability of occurrence correspond to the days and the areas of real landslides.
The application has also highlighted some drawbacks that are mainly related to the validation of the model performance and to the uncertainty of the model input parameters. In particular, a satisfactory validation of the model is only possible if a complete event database of landslides with spatial and temporal resolution equal to the HIRESSS model resolutions is available. Furthermore, a correct geotechnical and hydrological characterization of the soil parameters as input data for the model, as well as a correct approach to spatializing the data are both fundamental to applying the model and obtaining sound result at the regional scale.
The data used in this paper can be requested from the corresponding author.
TS has developed the model code, performed the simulations and wrote the paper. VT coordinated and conceived the work and wrote the paper. GR developed the model code and performed the simulation. MA, CTS, EBM, AR, VP, PV, MP carried out the in situ and laboratory tests and prepared the model input data. SR and HS provided the data for the simulation and relevant information related to the landslides in Aosta Valley. FC and NC supervised the work.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Landslide early warning systems: monitoring systems, rainfall thresholds, warning models, performance evaluation and risk perception”. It is not associated with a conference.
This research has been carried out in the framework of a research agreement
between the Department of Earth Sciences of the University of Firenze, and
the Centro funzionale, Regione Autonoma Valle d'Aosta. We would like to thank
the editor and three anonymous referees for their suggestions and careful
revisions.
Edited by: Luca Piciullo
Reviewed by: three
anonymous referees
Aleotti, P.: A warning system for rainfall-induced shallow failures, Eng. Geol., 73, 247–265, https://doi.org/10.1016/j.enggeo.2004.01.007, 2004.
Amoozegar, A.: Compact constant head permeameter for measuring saturated hydraulic conductivity of the vadose zone, Soil Sci. Soc. Am. J., 53, 1356–1361, 1989.
Arnone, E., Noto, L. V., Lepore, C., and Bras, R. L.: Physically- based and distributed approach to analyse rainfall-triggered land- slides at watershed scale, Geomorphology, 133, 3–4, 121–131, 2011.
Baroni, G., Facchi, A., Gandolfi, C., Ortuani, B., Horeschi, D., and van Dam, J. C.: Uncertainty in the determination of soil hydraulic parameters and its influence on the performance of two hydrological models of different complexity, Hydrol. Earth Syst. Sci., 14, 251–270, https://doi.org/10.5194/hess-14-251-2010, 2010.
Baum, R., Savage, W., and Godt, J.: Trigrs: A FORTRAN program for transient rainfall infiltration and grid-based regional slope – stability analysis, Open-file Report, US Geol. Survey, 2002, USGS Open-File Report 02-424, Reston, VA, available at: http://pubs.usgs.gov/of/2002/ofr-02-424/ (last access: 7 December 2016), 2002.
Baum, R. L. and Godt, J. W.: Early warning of rainfall-induced shallow landslides and debris flows in the USA, Landslides, 7, 259–272, 2010.
Bicocchi, G., D'Ambrosio, M., Rossi, G., Rosi, A., Tacconi Stefanelli, C., Segoni, S., Nocentini, M., Vannocci, P., Tofani, V., Casagli, N., and Catani, F.: Geotechnical in situ measures to improve landslides forecasting models: A case study in Tuscany (Central Italy), Landslides and Engineered Slopes, Experience, Theory and Practice, 2, 419–424, 2016.
Bischetti, G. B., Chiaradia, E. A., and Epis, T.: Prove di trazione su radici di esemplari di piante pratiarmati, Rapporto interno, Istituto di Idraulica Agraria, Università degli Studi di Milano, 2009.
Burylo, M.: Relations entre les traits fonctionnels des espèces végétales et leurs fonctions de protection contre l'erosion dans le milieu marneux restaurés de montagne, Dissertation, University of Grenoble, France, 2010.
Cannon, S. H., Boldt, E. M., Laber, J. L., Kean, J. W., and Staley, D. M.: Rainfall intensity – duration thresholds for postfire debris – flow emergency-response planning, Nat. Hazards, 59, 209–236, 2011.
Carrara, A., Crosta, G., and Frattini, P.: Comparing models of debris-flow susceptibility in the alpine environment, Geomorphology 94, 353–378, 2008.
Catani, F., Segoni, S., and Falorni, G.: An empirical geomorphology-based approach to the spatial prediction of soil thickness at catchment scale, Water Resour. Res., 46, W05508, https://doi.org/10.1029/2008WR007450, 2010.
De Giusti, F., Dal Piaz, G. V., Massironi, M., and Schiavo, A.: Carta geotettonica della Valle d'Aosta alla scala 1 : 150.000, Mem. Sci. Geol., 55, 129–149, 2004.
Del Soldato, M., Segoni, S., De Vita, P., Pazzi, V., Tofani, V., and Moretti, S.: Thickness model of pyroclastic soils along mountain slopes of Campania (southern Italy), in: Landslides and Engineered Slopes, Experience, Theory and Practice, Associazione Geotecnica Italaian, Aversa, et al. (Eds.), Rome, Italy, 797–804, 2016.
Dietrich, W. and Montgomery, D.: Shalstab: a digital terrain model for mapping shallow landslide potential, NCASI (National Council of the Paper Industry for Air and Stream Improvement) Technical Report, February, 1998.
Fanelli, G., Salciarini, D., and Tamagnini, C.: Reliable soil property maps over large areas: a case study in Central Italy, Enviro. Eng. Geosci., 22, 37–52, https://doi.org/10.2113/gseegeosci.22.1.37, 2016.
Giadrossich, F., Preti, F., Guastini, E., and Vannocci, P.: Metodologie sperimentali per l'esecuzione di prove di taglio diretto su terre rinforzate con radici, Experimental methodologies for the direct shear tests on soils reinforced by roots, Geologia tecnica & ambientale, 4, 5–12, 2010.
Gray, D. H. and Ohashi, H.: Mechanics of fiber reinforcement in sand, J. Geotech. Eng., 109, 335–353, 1983.
Jiang, S. H., Li, D. Q., Zhang, L. M., Zhou, C. B.: Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method, Eng. Geol, 168, 120–128, 2013.
Lagomarsino, D., Segoni, S., Fanti, R., and Catani, F.: Updating and tuning a regional scale landslide early warning system, Landslides, 10, 91–97, 2013.
Lu, N. and Godt, J. W.: Infinite-slope stability under steady unsaturated seepage conditions, Water Resour. Res., 44, W11404, https://doi.org/10.1029/2008WR006976, 2008.
Martelloni, G., Segoni, S., Fanti, R., and Catani, F.: Rainfall thresholds for the forecasting of landslide occurrence at regional scale, Landslides, 9, 485–495, 2012.
Mercogliano, P., Segoni, S., Rossi, G., Sikorsky, B., Tofani, V., Schiano, P., Catani, F., and Casagli, N.: Brief communication “A prototype forecasting chain for rainfall induced shallow landslides”, Nat. Hazards Earth Syst. Sci., 13, 771–777, https://doi.org/10.5194/nhess-13-771-2013, 2013.
Operstein, V. and Frydman, S.: The influence of vegetation on soil strength, Ground Improv., 4, 81–89, 2000.
Pack, R. T., Tarboton, D. G., and Goodwin, C. N.: Assessing terrain stability in a gis using sinmap, in: “15th Annual GIS Conference, GIS 2001, Vancouver, British Columbia, Canada, 2001.
Park, H. J., Lee, J. H., and Woo, I.: Assessment of rainfall-induced shallow landslide susceptibility using a GIS-based probabilistic approach, Eng. Geol., 161, 1–15, 2013.
Pollen, N., Simon, A., and Collison, A. J. C.: Advances in assessing the mechanical and hydrologic effects of riparian vegetation on streambank stability, in: Riparian Vegetation and Fluvial Geomorphology, Water Sci. Appl. Ser., edited by: Bennett, S. and Simon, A., AGU, Washington, D. C., 8, 125–139, 2004.
Rawls, W. J., Brakensiek, D. L., and Saxton, K. E.: Estimating soil water properties, Transactions, ASAE, 25, 1316–1320 and p. 1328, 1982.
Ren, D., Fu, R., Leslie, L. M., Dickinson, R., and Xin, X.: A storm-triggered landslide monitoring and prediction system: formulation and case study, Earth Interact., 14, 1–24, 2010.
Rhynsburger, D.: Analytic delineation of Thiessen polygons, Geogr. Anal., 5, 133–144, 1973.
Richards, L. A.: Capillary conduction of liquids through porous mediums, PhD Thesis, Cornell University, New York, 1931.
Rosi, A., Segoni, S., Catani, F., and Casagli, N.: Statistical and envi- ronmental analyses for the definition of a regional rainfall thresholds system for landslide triggering in Tuscany (Italy), J. Geogr. Sci., 22, 617–629, 2012.
Rossi, G., Catani, F., Leoni, L., Segoni, S., and Tofani, V.: HIRESSS: a physically based slope stability simulator for HPC applications, Nat. Hazards Earth Syst. Sci., 13, 151–166, https://doi.org/10.5194/nhess-13-151-2013, 2013.
Salciarini, D., Tamagnini, C., Conversini, P., and Rapinesi, S.: Spatially distributed rainfall thresholds for the initiation of shallow landslides, Nat. Hazards, 61, 229–245, https://doi.org/10.1007/s11069-011-9739-2, 2012.
Salciarini, D., Fanelli, G., and Tamagnini, C.: A probabilistic model for rainfall-induced shallow landslide prediction at the regional scale, Landslides, 14,1731–1746, https://doi.org/10.1007/s10346-017-0812-0, 2017.
Segoni, S., Leoni, L., Benedetti, A. I., Catani, F., Righini, G., Falorni, G., Gabellani, S., Rudari, R., Silvestro, F., and Rebora, N.: Towards a definition of a real-time forecasting network for rainfall induced shallow landslides, Nat. Hazards Earth Syst. Sci., 9, 2119–2133, https://doi.org/10.5194/nhess-9-2119-2009, 2009.
Simoni, S., Zanotti, F., Bertoldi, G., and Rigon, R.: Modelling the probability of occurrence of shallow landslides and channelized debris flows using GEOtop-FS, Hydrol. Process., 22, 532–545, 2008.
Tofani, V., Bicocchi, G., Rossi, G., Segoni, S., D'Ambrosio, M., Casagli, N., and Catani, F.: Soil characterization for shallow landslides modeling: a case study in the Northern Apennines (Central Italy), Landslides, 14, 755–770, https://doi.org/10.1007/s10346-017-0809-8, 2017.
Vergani, C., Bassanelli, C., Rossi, L., Chiaradia, E. A., and Bischetti, G. B.: The effect of chestnut coppice forest abandon on slope stability: a case study, Geophys. Res Abstr, 15, EGU2013-10151, 2013.
Vergani, C., Giadrossich, F., Schwarz, M., Buckley, P., Conedera, M., Pividori, M., Salbitano, F., Rauch, H. S., and Lovreglio, R.: Root reinforcement dynamics of European coppice woodlands and their effect on shallow landslides, a review, Earth Sci. Rev., 167, 88–102, https://doi.org/10.1016/j.earscirev.2017.02.002, 2017.
Wagner, A. A.: The use of the Unified Soil Classification System by the Bureau of Reclamation, Proc. 4th Intern. Conf. Soil Mech. Found. Eng., London, 1, 125, 1957.
Waldron, L. J. and Dakessian, S.: Soil reinforcement by roots: calculations of increased soil shear resistance from root properties, Soil Sci., 132, 427–435, 1981.