the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
New experimental diagnostics in combustion of forest fuels: microscale appreciation for a macroscale approach
Dominique Cancellieri
Valérie Leroy-Cancellieri
Xavier Silvani
Frédéric Morandini
In modelling the wildfire behaviour, good knowledge of the mechanisms and the kinetic parameters controlling the thermal decomposition of forest fuel is of great importance. The kinetic modelling is based on the mass-loss rate, which defines the mass-source term of combustible gases that supply the flames and influences the propagation of wildland fires. In this work, we investigated the thermal degradation of three different fuels using a multi-scale approach.
Lab-scale experimental diagnostics such as thermogravimetric analysis (TGA), differential scanning calorimetry (DSC), use of the cone calorimeter (CC) or Fire Propagation Apparatus (FPA) led to valuable results for modelling the thermal degradation of vegetal fuels and allowed several upgrades of pyrolysis models.
However, this work remains beyond large-scale conditions of a wildland or forest fire. In an effort to elaborate on the kinetic models under realistic natural fire conditions, a mass-loss device specifically designed for the field scale has been developed. The paper presents primary results gained using this new device, during large-scale experiments of controlled fires. The mass-loss records obtained on a field scale highlight the influence of the chemical composition and the structure of plants. Indeed, two species with similar chemical and morphological characteristics exhibit similar mass-loss rates, whereas the third presents different thermal behaviour.
The experimental data collected at a field scale led to a new insight about thermal degradation processes of natural fuel when compared to the kinetic laws established in TGA. These new results provide a global description of the kinetics of degradation of Mediterranean forest fuels. The results led to a proposed thermal degradation mechanism that has also been validated on a larger scale.
In studying the forest fire propagation, kinetic modelling of thermal degradation mechanisms is one of the main prerequisites for the determination of source terms, allowing for the development of realistic models. Numerous computational fluid dynamics (CFD) codes have been developed for predicting the fire spread, the heat release and providing operational tools for the land managers (Linn et al., 2002; Mell et al., 2007). Indeed, physically based models, initiated by Grishin (1997), account for each mechanism of heat transfer individually and predict not only the spread rate of the fire but also its complete behaviour. The thermal degradation of the solid phase as well as the combustion of the gaseous pyrolysis products are described, requiring the development of specific kinetic models for the vegetation fuels. Appropriate kinetic mechanisms should be coupled with the description of transport mechanisms (heat-, mass- and momentum-transfer) to provide a more detailed process simulation. The mass-loss rate of the solid phase is one of the most important parameters in describing the evolution of the solid phase. Indeed, it is directly linked to the mass-loss rate due to pyrolysis and represents the initial factor of the combustion process. These parameters are often determined from small-scale tests such as thermogravimetric analysis (TGA).
TGA is a thermoanalytical technique commonly used in solid-phase thermal degradation studies (Ninan, 1989; White et al., 2011). It has gained widespread attention in the thermal analysis of biomass pyrolysis (Di Blasi, 2008; White et al., 2011). TGA measures a decrease in the substrate mass caused by the release of volatiles (devolatilisation) during thermal decomposition. In practice, the mass of the sample being heated at a specific rate is monitored as a function of temperature or time. TGA requires sufficiently small samples for the diffusion effects to be negligible and for the pyrolysis process to be kinetically controlled (Miller and Bellan, 1997). The experimental data collected under perfectly controlled TGA conditions ensure an accurate determination of the kinetic mechanism. Unfortunately, these experimental conditions are not realistic in terms of heating rate with those encountered in forest fire. Sometimes, calorimetric experiments are performed with a cone calorimeter (CC) (Schemel et al., 2008) or a Fire Propagation Apparatus (FPA) (Simeoni et al., 2012), but the gap to the real scale is still significant.
Overall, field data collection is demanding and potentially dangerous; however, it is considered the best alternative for improving and validating the fire spread models (Morandini et al., 2006). Consequently, a number of field tools have been proposed, such as thermocouples, heat flux gauges (Silvani et al., 2009), gas sensors (Miranda et al., 2010) and audio and video sensors (Stavrakakis et al., 2014).
In order to preserve the plant structure some authors have carried out tests on trees (Mell et al., 2009) or litter (Dupuy, 1995), but the ignition conditions are not similar to those encountered during a wildfire. However, according to our knowledge, accuracy measurements of mass loss have never be done in field experiment conditions.
In view of these limitations, the aim of this study is to propose kinetic models adapted to realistic Mediterranean forest fire conditions. A mass-loss device specifically designed for a field scale has been developed for this purpose. This device can record the mass loss and temperatures of three vegetation samples submitted to a heat flux from a spreading flame front across a large bed of fuel. One of the main advantage of this system is to simultaneously submit three different samples to the same fire front and in identical meteorological conditions, which greatly facilitates the comparison of the thermal behaviours. The choice of this heat flux source allowed a better correspondence with forest fire conditions to be achieved. This system can provide characteristic dynamic data such as temperature and mass-loss rate.
In the first step reactional mechanisms are defined from experiments performed in perfectly controlled conditions on thermal thin samples (in TGA). Using these experimental data, kinetic models are proposed for each species. Due to these models, the simulation of the mass-loss rate is done at the same high heating rates as those measured during the field experiment. In the last step, the mass-loss rates obtained from the simulation are compared to the experimental data collected on a field scale.
Very few studies are focused on the mass loss measurement of biomass obtained during a field fire experiment.
2.1 Samples
The forest fuels used were representative of the Mediterranean region. We selected three species with different physiological structures: rockrose (Cistus monspeliensis), heather (Erica arborea), pine (Pinus pinaster). The forest fuels were collected from live shrubs or trees in forests close to the University of Corsica. The experiments were performed using branches and twigs with leaves or needles still attached. Some authors have demonstrated that only small particles (< 6 mm) govern the dynamic of fire spread (Burrows, 2001; Morvan and Dupuy, 2004). According to this observation we have decided to sample the foliage and aerial parts of each species. The proportions of leaves and twigs vary for each specie, at around 50 % leaves for heather and rockrose due to their similar structures. Conversely, 75 % of pine is composed of needles as opposed to twigs. In order to highlight the different structures of the species, Fig. 1 presents a picture of each specie.
In order to focus on oxidative pyrolysis and combustion processes, samples were oven-dried for 24 h at 333 K (Leroy-Cancellieri et al., 2014). This sample state allows the dehydration phenomenon to be suppressed and thus the influence of the moisture content on the burning. Moreover, getting rid of the moisture content lets us concentrate on the influence of the physicochemical parameters of plants on the burning rate. Collected samples were then brought to the laboratory, washed with deionised water and oven dried for 12 h at 333 K. After these preparation stages, the sampling has been separated into two cases:
-
For field experiments, the aim was to keep the conditions encountered during wildland fire, so we have used an intact branch of a dried plant in order to be close as possible to their natural state. For each specie, only one branch is directly placed on the prototype tube. The initial mass of the samples is approximately 50 ± 0.001 g, which is larger than that of the samples by a factor of around 10 000 for the experiments performed at the laboratory scale. According to the species it represents a branch about 20 cm high (cf. Fig. 1).
-
For the TGA experiments, dried samples were ground and sieved to pass through a 100 µm mesh, then kept in the desiccator to protect them from ambient humidity. The sieved powdery sample was stored in airtight plastic containers for future use.
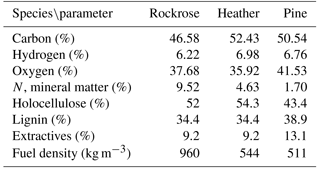
The moisture content arising from self-rehydration was about 4 % for all samples before testing. The chemical and physiological properties play a significant role in thermal decomposition of fuel, so a characterisation of the studied species, including elemental and lignocellulosic composition and physiologic properties, has been performed. Lignocellulosic materials were determined by different gravimetric methods, according to normalised (Ona et al., 1994; TAPPI, 1974) or published methods (Peterssen, 1984; Wise et al., 1946). The density was measured following the methodology proposed by Moro (2006). The elemental analysis was carried out at the SCA (Service Central d'Analyse) USR 59 CNRS, and the results are shown in Table 1.
2.2 Laboratory experiments
Mass loss is one of the main parameters used for the kinetic characterisation of thermal degradation mechanisms. It is known as the major driving parameter for the characterisation of source terms. Moreover, the mass loss provides qualitative and quantitative data on different reactions which take place in the heated solid phase (Kissinger, 1957). In order to investigate the mass-loss behaviour, thermogravimetric experiments were carried out in a thermogravimetric analyser (PerkinElmer, Pyris 1 TGA). For each sample, 5 mg of dried above-ground biomass was heated from 350 to 900 K under dynamic conditions at a heating rate of 30 K min−1. The TGA furnace was flushed with air at a rate of 20 mL min−1 to maintain the oxidative atmosphere for thermal degradation of particles in the course of experiments. Each experiment was repeated at least thrice with excellent reproducibility higher than 99.7 %. The precision of temperature measurements was ±2 K.
2.3 Field experiments
To investigate the scale effect and to highlight the similarities and differences between laboratory and field experiments, a device especially designed for field has been created. It allows the mass loss and temperature to be simultaneously recorded when samples are exposed to a heat source. In order to achieve the real fire conditions, the heat source is a fire front. The description of this mass-loss prototype and its usage is detailed in the following sections.
2.3.1 Differential mass-loss prototype set-up
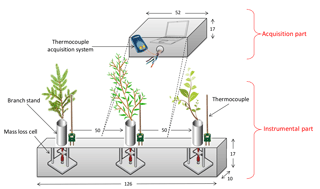
The prototype consists of two parts: the one responsible for measurements and the one responsible for data acquisition. The characteristics of each part are given below. Figure 2 depicts the entire mass-loss prototype.
Analogue measurement devices
The device was sized to be one-fifth the width of the plot to burn. This ensures that the fire completely encompasses the system during its propagation.
The device includes three load cells integrated in a welded ceramic box (1260 mm × 170 mm × 100 mm), covered with a 50 mm thick refractory lining (Thermal Ceramics Kaowool 1600).
Taking into account the fact that the meteorological and fire conditions are difficult to reproduce perfectly, we decided to install the three load cells on the apparatus to follow the behaviour of three species subjected to the same fire propagation. With such three species available in the prototype, the differential analysis between the samples can be performed independently of the external conditions.
The three load cells (LSB 200, Futek®) have a maximum capacity of 450 g ± 0.1 % and a width of 6.8 mm, a height of 19 mm and a length of 17.5 mm. Samples are introduced in the load cells through the stainless tube mounted on top of each cell. The height and the diameter of this tube (190 mm × 20 mm) were reckoned up to avoid any lift effect. Moreover, the position and the height of the sample in the tube can be adjusted to optimise the interaction between the flame and the sample.
The distance between each supporting tube (500 mm) was chosen such that the decomposition of a particular branch could not affect the neighbouring branch. Thus, the plant will only be affected by the fire front in front of the device.
To measure the temperature acting on the sample and the heating rate of the fire, another tube, accommodating a thermocouple, is placed very close to the tube supporting the branch. The thermocouple, positioned in a vertical position can be adjusted in height. With the possibility of adjusting each element (branch and thermocouple), we ensured that the thermocouple is positioned at the middle of the branch. This configuration ensures the determination of the real temperature to which the sample is subjected.
The K-type thermocouples were selected according to their temperature range, with an upper limit of 1300 ± 0.5 ∘C (Omega® HKMTSS-010G-8, diameter: 25 µm).
Data acquisition and process
The acquisition system is integrated into a thermal box with a Multilayer Aluminization (Z-Flex®) shield. A remote wireless acquisition system is actually impossible to use because of the disturbances introduced by the thermal shield. The temperature inside the thermal box is controlled using a thermocouple. If necessary, it is adjusted by a fan when the temperature of the thermal box is rising. A laptop located inside the box is used to transmit the data simultaneously through a USB interface using custom software.
The mass-loss data are recorded using the Sensit software of Futek with a frequency of 2.5 Hz.
The temperature data are synchronised with the mass-loss data recorded with the same frequency, using the acquisition unit Omega® TC-08. This system can accommodate up to eight thermocouples with an acquisition frequency of 10 Hz.
One of the main advantages of this prototype is that three different species can be subjected to the same external heating conditions in line and be analysed simultaneously under the same field conditions.
2.3.2 Experimental and meteorological conditions
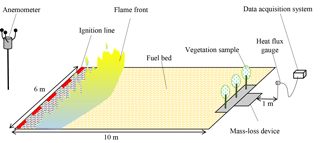
The field tests took place in an open-field terrain with no slope, situated in the Unit Instruction and Civil Security Intervention No. 5 of Corte in Corsica. The three species are subjected to the same heat source: the fire spreading over a wood-wool bed. This fuel was selected for reasons of good repeatability of the heating conditions.
About 120 kg of wood wool was used, forming a bed of 10 m at length and almost 6 m at width. The average height of the bed has been appropriately selected to comply with a fuel load of 2 kg m−2. The orientation of the fuel bed was based on the meteorological forecast of the day of the experiment, following the wind direction. A linear ignition was performed at the bottom of the wood-wool bed.
The wind velocity and direction were recorded using a two-dimensional ultrasonic anemometer at 2.5 m above the ground surface to reflect the average wind acting on the fire front. The anemometer was located in the direction of the propagation (at the end of the plot). The wind data were recorded using another (synchronised) data logger at a sampling rate of 1 Hz. The average velocity of the wind measured during the experiment was 1.2 m s−1 and its direction was close to the south-east (143∘). During the campaign the wind was relatively constant with a standard deviation of 0.44 m s−1.
Heat flux measurement
Three types of thermal transfer occur during the spread of a natural fire. Because the paper focuses on the thermal degradation governed by a heat source external to the sample, the heat transfer inside the flame front were not considered in the present work. Beyond that, it is first important to explain here why we chose to focus on radiation and convection. Heat conduction in a solid fuel is usually not considered in the set of transport phenomena involved in the spread of a natural fire as detailed in Silvani et al. (2012).
Furthermore, this previous work on thermal transfer from a fire to a bed of pine excelsior was already performed in similar no slope, no wind conditions and with comparable fuel loads (Silvani et al., 2012).
This study exhibits that the heat transfer is mainly due the thermal radiation from the fire. At such scales, the vegetal fuel is also known to absorb the heat radiation according coefficients to black-body conditions (Boulet et al., 2011).
The measurements of the heat fluxes emitted from the flame front during the fire spread are therefore measured using radiant heat flux gauge from Medtherm. It consists of a total heat flux gauge upon which a special window is used in order to eliminate the convective heat transferred to the sensing area. As in the present case, the use of a sapphire window was especially appropriate for detecting the radiative properties of a natural fire at the bench scale. Spectral emission experiments (Boulet et al., 2011) conducted on flames and their related burning bed of excelsior and vine branches illustrate that, first, the main radiation proceeds from the flame, and second, flames and fuel beds mainly emit in the wave number ranges of 2000–2300 and 1500–6000 cm−1. The sapphire window [1.2; 5.5 µm] was therefore convenient for the present study because it transmitted thermal radiation emitted in the wave number range of 1800–8333 cm−1. The radiant heat flux emitted from the flame front during fire spread was measured using a transducer located at 1 m from the end of fuel bed. The measurement height was 0.5 m. The heat flux measurements were recorded using a data logger at a sampling rate of 1 Hz.
The transducer was calibrated by the manufacturer in the range of 0–200 kW m−2 and had a response time lower than 0.25 s. Because the radiant gauge was calibrated using its sapphire window (with a 3 % error for the incident heat flux in the range 0–150 kW m−2 and 10 % beyond this according to the manufacturer), no transmittance correction was needed for the heat flux density. Furthermore, as presented in the same reference, one cannot omit the possible contribution of faster fluctuations occurring on a larger scale than the present one due to the turbulent nature of the flow. At the end, one must accept that investigating the scale dependence on spectral properties in the heat transfer via radiation from natural fires remains a valuable open subject.
Under these limitations, the radiant heat flux gauge provided accurate measurements of the longitudinal component of the heat flux density when they faced an approaching fire front. The transducer was oriented toward the flame front and had a 150∘ viewing angle. The region viewed by the gauge, located at 1 from the litter's end, allowed us to measure the contribution of the whole fire front. Finally, a thermocouple recorded the body temperature of the gauge during fire tests; for controlling it worked in nominal conditions.
The devices deployed on the site are depicted in Fig. 3, which presents the overall experimental set-up.

Figure 4Differential mass-loss prototype placed in the middle (a) and at the end (b) of the fuel bed.
The position of the prototype within the plot was tested in different configurations: the device was first placed in the middle of the field but the steady-state conditions of the fire propagation were not obtained. Then positioning at the other end of the plot was tried but we observed an edge effect due to the lack of litter behind the prototype. Figure 4 shows pictures of the device during configuration of these two tests.
Finally, the prototype has been placed near the end of the fuel bed to ensure steady-state propagation without the edge effect.
The experiments were performed in an area with no slope and were replicated three times on the same day to ensure identical surrounding conditions.
3.1 Laboratory experiments
Using TGA, the thermal degradation in air is characterised by a continuous weight loss until the point at which the weight becomes almost constant. The first derivative of such thermogravimetric curves (i.e. −dm∕dt) yields the maximum reaction rate. This procedure is known as derivative thermogravimetry (DTG). The character of the TGA curve, in combination with the corresponding DTG peaks, gives a clear indication of the number of stages in thermal degradation.
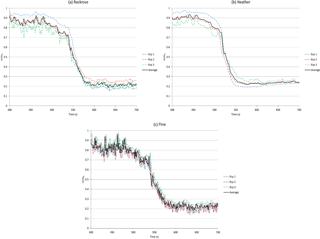
Figure 5 presents the experimental results on the thermal degradation of fuels heated at 30 K min−1 from 350 to 900 K under air sweeping.
Clear similarities in the decomposition process can be observed for the three species. They imply that there could be a general kinetic scheme to describe biomass thermochemical degradation under air atmosphere. TGA curves exhibit two stages of weight loss, which are confirmed in DTG by two peaks (cf. Fig. 5). Despite the complex chemical process, experimental data suggest that a two-step model of global reactions can describe the most important features of the thermal and oxidative degradation of plants. The first mass loss due to decomposition begins slowly and accelerates rapidly in the temperature range of 500–550 K. The second mass loss follows the first one and reaches an overall mass loss of more than 90 %. Moreover, the oxidative process is claimed to have two stages. The first stage is the volatilisation of the main biomass compounds and the production of charcoal (char) residue at low temperatures. The second stage includes the decomposition of lignin and the combustion of the charcoal produced at the preceding stage (Fang et al., 2006). The same phenomena were observed and recorded by other authors as well (Branca and Di Blasi, 2004; Safi et al., 2004; Shen et al., 2009).
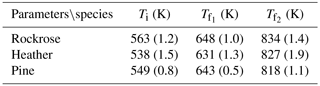
In order to compare biomass thermal behaviour, DTG is frequently used to determine several temperature indexes: ignition temperature (Ti), final temperature of the first process (), final temperature of the second process (). Ti is defined as the inflection point of DTG at the start of the degradation, while are defined as the inflection points at the end of each stage.
For the heating rate considered in this study, the onset temperature is the lowest for heather, higher for pine and even higher for rockrose. This observation can be used as the ignition criterion, since the onset temperature marks out the beginning of oxidation reactions. The fuels with low onset temperatures are most ignitable, and they burn easily. These results will be compared to the field-scale experiments.
Using the TGA data, a kinetic model for each specie will be done in Sect. 4.
3.2 Field experiments
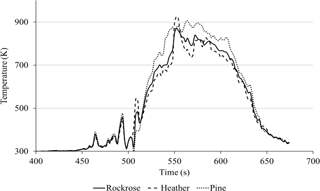
Figure 6 presents the average temperature as a function of time, according to the data recorded while the plot was burning.
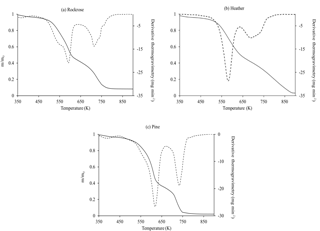
Figure 5TGA (lines) and DTG (dotted) of oven-dried rockrose (a), heather (b) and pine (c) samples obtained with a linear heating rate of 30 K min−1 under air atmosphere.
The temperature profiles were nearly the same for the three species with a maximum at 926 K. The behaviour of the temperature indicates that the effect of the fire front on the prototype can be considered a straight line. Using the evolution of temperature during the course of the experiment, the heating rate was estimated for each plant. The average of the heating rates during the heating phase were obtained: 13.2 K s−1 for pine, 12.9 K s−1 for heather and 12.1 K s−1 for rockrose. The heating rate can be approximate at a median value of 12.7 ± 0.6 K s−1 for all species. This result accredits the fact that the temperature measurement in three points with a 500 mm difference is homogenous along the whole test field.
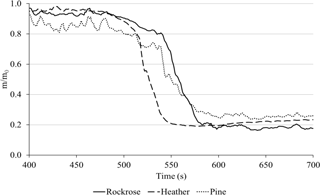
Figure 7 demonstrates the mass loss synchronised to the temperature vs. time data shown above. The figure exhibits, for each specie, the records of the three experiments and their averages, with a confidence level lower than 16 %.
In order to facilitate the comparison between the fuels, Fig. 8 shows the average mass loss on the same graph.
Heather starts to lose its mass more quickly than rockrose and pine. This observation is in agreement with the laboratory experiments and ignition temperature provided in Table 2. Indeed, heather exhibits a low onset temperature, implying that this species will ignite prior to the two other species. The behaviour exhibited in TGA is similar to the one observed on the field scale. The order of the rate of degradation among species determined at the laboratory scale is kept on the field scale (the degradation is faster for heather and rockrose, and it is slower for pine).
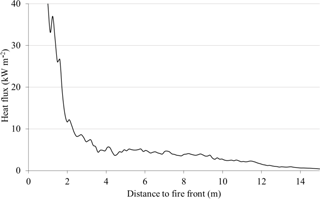
The main advantage for the field experiments is the exposure of samples to a real fire front so it is of importance to have the measures of heat flux records during the experimental tests. The average longitudinal distribution of radiant heat flux impinging ahead of the flame front is provided in Fig. 9.
Preheating the fuel via radiation is a long-range process. The main advantage of such fire experiments in the field is to allow the samples of vegetative fuel to be exposed to thermal conditions characteristic of a spreading wildfire (Silvani et al., 2009). For the configuration considered in the present study, the rise of temperature in the fuel elements can occur far from the fire front since sufficient radiation levels (> 5 kW m−2) are measured at a distance of 6 m, and pyrolysis can begin within 2 m from the fire front. Indeed, piloted auto-ignition of such fuels was observed for laboratory-scale experiments for impinging heat fluxes in the range of 20–25 kW m−2 (Bartoli et al., 2011). It should be noted that, even if high radiation levels of the same order of magnitude can be obtained in the laboratory using radiant heaters, the heating rates are not representative of a travelling fire front since samples are submitted to a constant heat flux.
Thermogravimetric data were used to find the best set of kinetic parameters for our three species. Using TGA measurements, the conversion degree α is defined as
with m the mass, m0 the initial mass and mf the final mass of the sample.
When the TGA experiments are conducted under non-isothermal conditions, the rate of heterogeneous solid-state reactions can be described as
where f(α) is the conversion function (reaction model), A is the pre-exponential factor, Ea is the activation energy, R is the universal gas constant, and β is the heating rate.
The kinetic parameters A, Ea and f(α) can be estimated from the TGA experimental data with a variety of techniques (Vyazovkin et al., 2011; Vyazovkin and Wight, 1998). To obtain a reliable kinetic description of the processes under investigation, we used an approach that combines accurate isoconversional methods with model-fitting methods (Chrissafis, 2009; Pratap et al., 2007). This two-step approach is the hybrid kinetic method (HKM), which was developed earlier by Cancellieri et al. (2005). At the first step, isoconversional methods provide Ea(α) and the reaction model. At the second step, these initial data are used in a model-fitting technique to obtain the pre-exponential factor and the nth-order model. This multi-step procedure allows a selection of the models that might otherwise be indistinguishable because of the poor quality of the regression fit when performed independently. In other words, this approach gives the highest probability of selecting the most accurate kinetic triplet (A, Ea and the model).
The laboratory experiments for our three species support the following two-step kinetic mechanism. The first process is modelled as
The second reaction deals with the oxidation of the char produced during the first process:
Both Reactions (R1) and (R2) can be described by the following differential equations (we consider an nth-order model):
The use of HKM allowed us to obtain the kinetic parameters listed in Table 3.
4.1 Comparisons
Considering the two-stage mechanism and the kinetic parameters listed in Table 3, the mass loss of each species can be simulated at the average heating rate measured during field experiment, which is 12.7 ± 0.6 K s−1 for all species. These numerical simulations were then compared to the experimental mass loss recorded on a field scale. Figure 10 compares the mass loss obtained experimentally for each species and the modelling data according to Eqs. (3) and (4).
Generally, simulations are in good agreement with the experimental mass-loss rate even if there are some differences (as an attempt). For rockrose, the model does not accurately fit the data in the range 0.85 > m∕m0 > 0.60, probably because the initiation and preheating mechanisms are more complex than in the model described by the simple Arrhenius equation of order n. For heather, experiments exhibit an accelerated degradation process which can be explained by the very fine structure of this species with branches as short as 2 mm. On the contrary, pine consists of single branches of 6 mm diameter. This sample thickness is responsible for the incomplete degradation.
The species are characterised in order to provide suitable input parameters. With accurate input parameters, models that implemented CFD codes could predict the propagation of fire. To obtain a reliable description of the processes and good agreement of the simulation, modellers need to know the mass-loss rate of the whole degradation. This parameter is defined as
with m the mass, t0 the initial time and tf the final time of the experiment.
To validate the kinetic mechanism and its parameters, the mass-loss rate obtained from field-scale experiments is compared to the one determined for the simulation performed with the kinetic model. These data are summarised in Table 4.
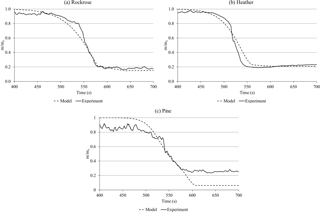
Figure 10Experimental (solid line) and modelled (dashed line) mass loss for (a) rockrose, (b) heather and (c) pine.
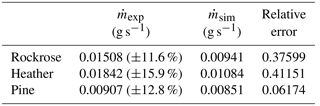
The main scope of this large-scale test campaign is to reveal the thermal behaviour of different species in the same experimental conditions. The data obtained in Table 4 highlight the importance of taking into account the physiological and chemical nature of species. Indeed, the mass-loss rate of pine is 50 % lower than heather and 40 % lower than the rockrose. The significant differences must be integrated into detailed physics-based models to ensure a reliable characterisation of the source terms.
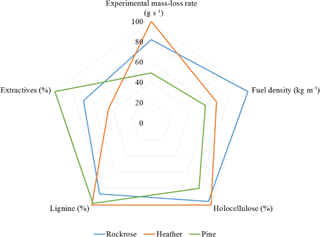
With the aim of providing guidelines for integration in detailed physics-based models, a radar chart has been used to graphically determine which chemical or structural parameters most impact the mass-loss rate. For coherence with the target element (), the graphic presented in Fig. 11 is only focused on the parameters directly linked with the mass loss: cellulose, lignin, holocellulose and fuel density. For more visibility, all the parameters have been dimensionless.
Figure 11 reveals that the holocellulose is the main impacting parameter on the mass-loss rate. Conversely, the extractive content is inversely proportional to mass-loss rate. Usually, physics-based models take into account fuel density, but it seems that the chemical composition and the structure of the plants are of primary interest when modelling wildland fire.
Stochastic conditions of fire imply great difficulty for the reproducibility of measurements. For these conditions, a differential mass-loss prototype has been designed with the aim to validate kinetic models adapted to the field scale. Comparative mass-loss data on three different plant species have never been recorded simultaneously. Moreover, it is the first time that the kinetics of the decomposition of biomass have been validated under real wildland fire conditions, thus ensuring reliable characterisation of source terms.
The technology presented in this paper is based on a completely new approach where the development of a new field mass-loss device, combined with recent progress in the understanding of the behaviour, achieves never before recorded data.
An experimental device, perfectly adapted to the biomass specificity has been developed based on a completely new differential approach. The prototype has been tested with three Mediterranean species. The results collected from field experiments emphasise the influence of various parameters such as the ignition temperature, biomass type and anatomical structure. However, the two-stage kinetic model based on the TGA data seems to fit the experimental data obtained at a field scale well. Using the field-scale measurements, the kinetic validity of the scheme is then extended outside TGA. This study allowed us to validate the kinetics of the decomposition of various biomasses under real wildland fire conditions, thus ensuring reliable characterisation of source terms. However, there were flawed predictions caused by the natural physiology of the samples (thickness and size of the leaves and branches). In fact, the initiation stage of preheating is strongly related to the physiology. Further studies will focus on the integration of sample thickness in the model as an inhibiting parameter.
The data used in this paper can be requested from the corresponding author.
DC conceived the original idea and supervised the project DC designed the mass-loss prototype. VLC wrote the paper with input from all authors. DC and VLC performed the TGA experiments and the numerical simulations. DC and VLC analysed the data. XS and FM carried out the fluxes measurements and analysed the recorded data. All the authors conceived and planned the field experiments. All the authors discussed the results and contributed to the final manuscript.
The authors declare that they have no conflict of interest.
The authors thank the Unit Instruction and Civil Security Intervention No. 5
of Corte in Corsica for the provision of their experimental field.
Edited by: Mario Parise
Reviewed by: two anonymous referees
Bartoli, P., Simeoni, A., Biteau, H., Torero, J. L., and Santoni, P. A.: Determination of the main parameters influencing forest fuel combustion dynamics, Fire Saf. J., 46, 27–33, https://doi.org/10.1016/j.firesaf.2010.05.002, 2011.
Boulet, P., Parent, G., Acem, Z., Collin, A., and Séro-Guillaume, O.: On the emission of radiation by flames and corresponding absorption by vegetation in forest fires, Fire Saf. J., 46, 21–26, https://doi.org/10.1016/j.firesaf.2010.03.006, 2011.
Branca, C. and Di Blasi, C.: Global interinsic kinetics of wood oxidation, Fuel, 83, 81–87, https://doi.org/10.1016/S0016-2361(03)00220-5, 2004.
Burrows, N. D.: Flame residence times and rates of weight loss of eucalypt forest fuel particles, Int. J. Wildland Fire, 10, 137–143, https://doi.org/10.1071/wf01005, 2001.
Cancellieri, D., Leoni, E., and Rossi, J. L.: Kinetics of the thermal degradation of Erica arborea by DSC: Hybrid kinetic method, Thermochim. Acta, 438, 41–50, https://doi.org/10.1016/j.tca.2005.07.013, 2005.
Cancellieri, D., Innocenti, E., and Leroy-Cancellieri, V.: WinGPYRO: A software platform for kinetic study of forest fuels, Fire Saf. J., 58, 103–111, https://doi.org/10.1016/j.firesaf.2013.01.005, 2013.
Chrissafis, K.: Kinetics of thermal degradation of polymers, J. Therm. Anal. Calorim., 95, 273–283, https://doi.org/10.1007/s10973-008-9041-z, 2009.
Di Blasi, C.: Modeling chemical and physical processes of wood and biomass pyrolysis, Prog. Energy Combust. Sci., 34, 47–90, https://doi.org/10.1016/j.pecs.2006.12.001, 2008.
Dupuy, J. L.: Slope and Fuel Load Effects on Fire Behavior: Laboratory Experiments in Pine Needles Fuel Beds, Int. J. Wildland Fire, 5, 153–164, https://doi.org/10.1071/wf9950153, 1995.
Fang, M. X., Shen, D. K., Li, Y. X., Yu, C. J., Luo, Z. Y., and Cen, K. F.: Kinetic study on pyrolysis and combustion of wood under different oxygen concentrations by using TG-FTIR analysis, J. Anal. Appl. Pyrolys., 77, 22–27, https://doi.org/10.1016/j.jaap.2005.12.010, 2006.
Grishin, A. M.: Mathematical modeling forest fire and new methods fighting them, Publishing House of the Tomsk University, F. Albini, Tomsk, Russia, 1997.
Kissinger, H. E.: Reaction kinetics in differential thermal analysis, Anal. Chem., 29, 1702–1706, 1957.
Leroy-Cancellieri, V., Cancellieri, D., Leoni, E., Simeoni, A., and Filkov, A. I.: Energetic potential and kinetic behavior of peats, J. Therm. Anal. Calorim., 117, 1497–1508, https://doi.org/10.1007/s10973-014-3912-2, 2014.
Linn, R., Reisner, J., Colman, J. J., and Winterkamp, J.: Studying wildfire behavior using FIRETEC, Int. J. Wildland Fire, 11, 233–246, https://doi.org/10.1071/wf02007, 2002.
Mell, W., Jenkins, M. A., Gould, J., and Cheney, P.: A physics-based approach to modelling grassland fires, Int. J. Wildland Fire, 16, 1–22, https://doi.org/10.1071/WF06002, 2007.
Mell, W., Maranghides, A., McDermott, R., and Manzello, S. L.: Numerical simulation and experiments of burning douglas fir trees, Combust. Flame, 156, 2023–2041, https://doi.org/10.1016/j.combustflame.2009.06.015, 2009.
Miller, R. S. and Bellan, J.: A Generalized Biomass Pyrolysis Model Based on Superimposed Cellulose, Hemicelluloseand Liqnin Kinetics, Combust. Sci. Technol., 126, 97–137, https://doi.org/10.1080/00102209708935670, 1997.
Miranda, A. I., Martins, V., Cascão, P., Amorim, J. H., Valente, J., Tavares, R., Borrego, C., Tchepel, O., Ferreira, A. J., Cordeiro, C. R., Viegas, D. X., Ribeiro, L. M., and Pita, L. P.: Monitoring of firefighters exposure to smoke during fire experiments in Portugal, Environ. Int., 36, 736–745, https://doi.org/10.1016/j.envint.2010.05.009, 2010.
Morandini, F., Silvani, X., Rossi, L., Santoni, P.-A., Simeoni, A., Balbi, J.-H., Louis Rossi, J. and Marcelli, T.: Fire spread experiment across Mediterranean shrub: Influence of wind on flame front properties, Fire Saf. J., 41, 229–235, https://doi.org/10.1016/j.firesaf.2006.01.006, 2006.
Moro, C.: Détermination des caractéristiques physiques de particules de quelques espèces forestières méditerrannéenes, technical report PIF2006-06, INRA Avignon Avignon, France, 2006.
Morvan, D. and Dupuy, J. L.: Modeling the propagation of a wildfire through a Mediterranean shrub using a multiphase formulation, Combust. Flame, 138, 199–210, https://doi.org/10.1016/j.combustflame.2004.05.001, 2004.
Ninan, K. N.: Kinetics of solid state thermal decomposition reactions, J. Therm. Anal., 35, 1267–1278, https://doi.org/10.1007/BF01913047, 1989.
Ona, T., Testsuya, S., Masaru, S., and Kazumi, F.: Small-scale method to determine the content of wood components from multiple eucalypt samples, Tappi Journal, Peachtree Corners, USA, 121–126, 1994.
Peterssen, R. C.: Chemical composition of wood. Chemistry of solid wood, R. M. Rowell, Madison, USA, p. 304, 1984.
Pratap, A., Lilly Shanker Rao, T., Lad, K., and Dhurandhar, H.: Isoconversional vs. Model fitting methods, J. Therm. Anal. Calorim., 89, 399–405, https://doi.org/10.1007/s10973-006-8160-7, 2007.
Safi, M. J., Mishra, I. M., and Prasad, B.: Global degradation kinetics of pine needles in air, Thermochim. Acta, 412, 155–162, https://doi.org/10.1016/j.tca.2003.09.017, 2004.
Schemel, C. F., Simeoni, A., Biteau, H., Rivera, J. D., and Torero, J. L.: A calorimetric study of wildland fuels, Exp. Therm. Fluid Sci., 32, 1381–1389, https://doi.org/10.1016/j.expthermflusci.2007.11.011, 2008.
Shen, D. K., Gu, S., Luo, K. H., Bridgwater, A. V., and Fang, M. X.: Kinetic study on thermal decomposition of woods in oxidative environment, Fuel, 88, 1024–1030, https://doi.org/10.1016/j.fuel.2008.10.034, 2009.
Silvani, X., Morandini, F., and Muzy, J.-F.: Wildfire spread experiments: Fluctuations in thermal measurements, Int. Commun. Heat Mass Transf., 36, 887–892, https://doi.org/10.1016/j.icheatmasstransfer.2009.06.008, 2009.
Silvani, X., Morandini, F., and Dupuy, J.-L.: Effects of slope on fire spread observed through video images and multiple-point thermal measurements, Exp. Therm. Fluid Sci., 41, 99–111, https://doi.org/10.1016/j.expthermflusci.2012.03.021, 2012.
Simeoni, A., Thomas, J. C., Bartoli, P., Borowieck, P., Reszka, P., Colella, F., Santoni, P. A., and Torero, J. L.: Flammability studies for wildland and wildland–urban interface fires applied to pine needles and solid polymers, Fire Saf. J., 54, 203–217, https://doi.org/10.1016/j.firesaf.2012.08.005, 2012.
Stavrakakis, P., Agapiou, A., Mikedi, K., Karma, S., Statheropoulos, M., Pallis, G. C., and Pappa, A.: A scale-up field experiment for the monitoring of a burning process using chemical, audio, and video sensors, Environ. Sci. Pollut. Res., 21, 891–900, https://doi.org/10.1007/s11356-013-1945-x, 2014.
TAPPI – Technical Association of the Pulp and Paper Industry: Acid insoluble lignin in wood and pulp, rapport T 222 05-74, Tappi Journal, Peachtree Corners, USA, 1974.
Vyazovkin, S. and Wight, C. A.: Isothermal and non-isothermal kinetics of thermally stimulated reactions of solids, Int. Rev. Phys. Chem., 17, 407–433, https://doi.org/10.1080/014423598230108, 1998.
Vyazovkin, S., Burnham, A. K., Criado, J. M., Pérez-Maqueda, L. A., Popescu, C., and Sbirrazzuoli, N.: ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data, Thermochim. Acta, 520, 1–19, https://doi.org/10.1016/j.tca.2011.03.034, 2011.
White, J. E., Catallo, W. J., and Legendre, B. L.: Biomass pyrolysis kinetics: A comparative critical review with relevant agricultural residue case studies, J. Anal. Appl. Pyrolys., 91, 1–33, https://doi.org/10.1016/j.jaap.2011.01.004, 2011.
Wise, L. E., Murphy, M., and D'Addieco, A. A.: Chlorite holocellulose, its fractionation and bearing on summative wood analysis and on studies on the hemicelluloses, Tappi Journal, Peachtree Corners, USA, p. 11, 1946.