Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: proposing hydro-meteorological thresholds

Bogaard, Thom; Greco, Roberto

doi:https://doi.org/10.5194/nhess-18-31-2018

NHESS | Articles | Volume 18, issue 1

Nat. Hazards Earth Syst. Sci., 18, 31-39, 2018
https://doi.org/10.5194/nhess-18-31-2018
© Author(s) 2018. This work is distributed under
the Creative Commons Attribution 4.0 License.

NHESS | Articles | Volume 18, issue 1

Invited perspectives 04 Jan 2018

Invited perspectives | 04 Jan 2018

Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: proposing hydro-meteorological thresholds

Landslide hazard assessment: proposing hydro-meteorological thresholds

Thom Bogaard¹ and Roberto Greco² Thom Bogaard and Roberto Greco Thom Bogaard¹ and Roberto Greco²

¹Water Resources Section, Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, the Netherlands
²Dipartimento di Ingegneria Civile Design Edilizia e Ambiente, Università degli Studi della Campania Luigi Vanvitelli, Aversa (CE), Italy

Received: 30 Jun 2017 – Discussion started: 18 Jul 2017 – Revised: 13 Nov 2017 – Accepted: 16 Nov 2017 – Published: 04 Jan 2018

Abstract

Back to toptop

Many shallow landslides and debris flows are precipitation initiated. Therefore, regional landslide hazard assessment is often based on empirically derived precipitation intensity-duration (ID) thresholds and landslide inventories. Generally, two features of precipitation events are plotted and labeled with (shallow) landslide occurrence or non-occurrence. Hereafter, a separation line or zone is drawn, mostly in logarithmic space. The practical background of ID is that often only meteorological information is available when analyzing (non-)occurrence of shallow landslides and, at the same time, it could be that precipitation information is a good proxy for both meteorological trigger and hydrological cause. Although applied in many case studies, this approach suffers from many false positives as well as limited physical process understanding. Some first steps towards a more hydrologically based approach have been proposed in the past, but these efforts received limited follow-up.

Therefore, the objective of our paper is to (a) critically analyze the concept of precipitation ID thresholds for shallow landslides and debris flows from a hydro-meteorological point of view and (b) propose a trigger–cause conceptual framework for lumped regional hydro-meteorological hazard assessment based on published examples and associated discussion. We discuss the ID thresholds in relation to return periods of precipitation, soil physics, and slope and catchment water balance. With this paper, we aim to contribute to the development of a stronger conceptual model for regional landslide hazard assessment based on physical process understanding and empirical data.

How to cite

How to cite.

1 Introduction

Back to toptop

Landsliding is one of the most abundant hazards having massive influence on socioeconomic functioning of society. Continuous development in mountain areas increases the exposure of people and properties to the landslide hazards, with precipitation-initiated landslides being the most common. On a regional scale, the possibility of a landslide to occur can be assessed in different ways (Chacón et al., 2006, for review): (1) heuristic, via susceptibility modeling; (2) empirical, lumped-statistical, by relating rainfall information to the observed occurrence (e.g., Caine, 1980; Wieczorek and Glade, 2005; Guzzetti et al., 2007, 2008, and reference therein); and (3) by spatially distributed physical-deterministic modeling (e.g., Anderson and Lloyd, 1991; Montgomery and Dietrich, 1994; Wu and Sidle, 1995; Borga et al., 1998; Burton and Bathurst, 1998; Pack et al., 1998; Van Beek, 2002; Baum et al., 2008). The heuristic models are mainly used in first assessments of (landslide) hazards for regional planning. They are based on readily available static information – like topography, lithology and land use – and then empirically related to a historical landslide database (if available). The dynamic predisposing factors, like actual wetness state of the potentially unstable slopes, are not taken into account. The physical-process-based models can take into account the dynamics of regional hazard assessment. Most of these models run spatially distributed hydrology–slope stability calculations, with different conceptualization and degrees of complexity for the representation of the physical processes. Typically, the hydrology in these models at catchment scale is not calibrated, or the calibration is restricted to the infiltration process or local groundwater levels (if monitored). In such cases, the correctness of the modeling is assessed from how well local displacements or possible failure areas can be predicted. With the increased availability of data and computational power, a range of these models have been published with increased levels of complexity and applicability (e.g., Frattini et al., 2004; Arnone et al., 2011; Lepore et al., 2013; von Ruette et al., 2013; Anagnostopoulos et al., 2015; Aristizábal et al., 2016; Fan et al., 2016). However, the practical application of such deterministic models, especially in terms of early-warning systems, is still limited to specific studies, due to the time effort and data demand.

The precipitation intensity-duration (ID) thresholds for landslide hazard assessment, however, see widespread application in early-warning systems, both at local and regional scales. They are based on analysis of the dynamic variables precipitation and landslide occurrence, and require a high-quality spatiotemporal landslide inventory and precipitation time series. Empirical-statistical precipitation thresholds are derived by plotting two characteristics of precipitation, usually intensity (mm h⁻¹ or mm day⁻¹) and duration (h or days), that have or have not resulted in landslides in a given area. The separation line, a deterministic threshold or a probabilistic transition zone, between precipitation events inducing landslides and events without hazards, is then drawn visually or by separation techniques. Due to the spread of information over several orders of magnitude, it is usually plotted in bi-logarithmic scale. Various precipitation ID thresholds for landslide initiation have been derived for different physiographic settings and at various spatial scales (e.g., Wieczorek and Glade, 2005; Guzzetti et al., 2007, 2008; Peruccacci et al., 2017; Rossi et al., 2017). The global and regional landslide precipitation ID thresholds encompass different types of landslides and a distinct variety of geological and environmental factors, such as lithology, soil depths and land use. The local ID thresholds are restricted more often to relatively homogeneous conditions and mass movement types.

However, several shortcomings are frequently recognized and discussed. For example, Berti et al. (2012) recognized the problem of looking at landslide occurrence and disregarding non-occurrence when applying the ID threshold. They used a Bayesian probability approach to derive the probabilistic transition, explicitly taking into account landslide occurrence and non-occurrence. Also the role of hydrology in landslide initiation, although often acknowledged to be of key importance, is usually not included in the statistical precipitation ID threshold approach. Several attempts to more explicitly include predisposing hydrological factors have been proposed, mainly by including measures for antecedent soil moisture content (e.g., Crozier and Eyles, 1980; Glade et al., 2000; Godt et al., 2006; Ponziani et al., 2012) or by splitting data sets into physiographic units like lithology, soil type, land use or season (e.g., Sidle and Ochiai, 2006; Baum and Godt, 2010; Napolitano et al., 2016; Peruccacci et al., 2017). These approaches have improved the predictive accuracy of the ID thresholds. However, to the authors' knowledge, such studies have not been subject to a more thorough analysis of the specific hydrological information needed for reliable local and regional hazard prediction.

Therefore, the objectives of this invited perspective are to (a) critically analyze the precipitation ID thresholds for shallow landslides and debris flows from a hydro-meteorological point of view and (b) propose a conceptual framework for lumped hydro-meteorological hazard assessment based on the concepts of trigger and cause. We will frame in this perspective some published examples and associated discussions, making reference to work by colleagues who have already explored this avenue. The aim of this paper is to contribute to the development of a stronger conceptual model for regional landslide hazard assessment based on physical process understanding, not only on empirical data.

1.1 Hydro-meteorological analysis of ID thresholds

1.1.1 Comparing ID thresholds with IDF curves

Both precipitation ID thresholds and precipitation intensity-duration-frequency (IDF) curves are empirical relationships linking the duration of a precipitation event, D, with its average intensity, $I = H / D$ , with H being the precipitation depth during the event. IDF curves are routinely used in storm water and flood management design and predictions, as they describe the relationship linking duration and mean intensity of precipitation events characterized by the same return period (Chow et al., 1988). Several functional expressions can be used to describe such a relationship (Bernard, 1932; Wenzel, 1982; Koutsoyiannis, 1998), most of which can be approximated, especially for durations longer than 1 h, as a power law:

\begin{matrix} (1) & I = A \times D^{B}, \end{matrix}

with B [-] being the slope of the log-plotted straight line and A [L∕T] a measure of the rain intensity of a rain event of unit duration.

Equation (1) is also adopted to describe precipitation ID thresholds, the difference being that the IDF curves are isolines of cumulative probability of precipitation events, whereas the ID plots are empirical thresholds for shallow landslides and debris flow occurrence. Figure 1 gives examples of IDF curves with a return period of 10 years from different places around the world. A common feature of the curves is that, regardless of geographic location, B ranges from −0.8 to −0.65 for rain durations longer than ∼ 1 h, while it levels off to around −0.5 for D≤ 1 h for most IDF curves. Note that IDF curves are mostly determined for rain durations up to 24 h. In the same graph, the upper envelope of the largest precipitation values ever observed (World Meteorological Organization, 1986) is plotted using the equation proposed by Brutsaert (2005), which has a smaller slope with B equal to −0.52.

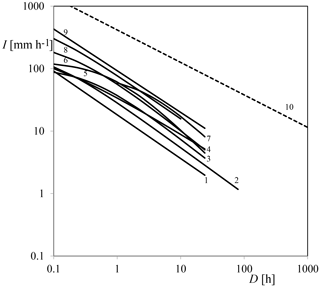
https://www.nat-hazards-earth-syst-sci.net/18/31/2018/nhess-18-31-2018-f01

Figure 1Examples of intensity-duration-frequency curves for a 10-year return period (1–9) and curve of the maximum observed precipitation (10). Location and source: 1 – Najran region, Saudi Arabia (Elsebaie, 2012); 2 – Uccle, Belgium (Van de Vyver, 2015); 3 – Naples, Italy (Rossi and Villani, 1994); 4 – Los Angeles, California (Wenzel, 1982); 5 – Pelotas, Brazil (Damé et al., 2016); 6 – New York (Wenzel, 1982); 7 – Hamada, Japan (Iida, 2004); 8 – Selangor, Malaysia (Chang et al., 2015); 9 – Sylhet, Bangladesh (Rasel and Hossain, 2015); 10 – greatest known observed point rainfall (Brutsaert, 2005).

Download

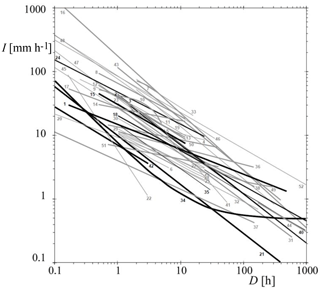
https://www.nat-hazards-earth-syst-sci.net/18/31/2018/nhess-18-31-2018-f02

Figure 2Rainfall intensity-duration (ID) thresholds. Numbers refer to case studies (Guzzetti et al., 2007). Very thick lines are global thresholds; thick lines are regional thresholds and thin lines are local thresholds. Black lines show global thresholds and thresholds determined for regions or areas pertaining to the central to eastern European region. Grey lines show thresholds determined for other regions or areas.

Download

More than 90 % of the landslides in the global data set are shallow landslides and debris flows (Fig. 2, Guzzetti et al., 2007). Note that the threshold is usually obtained as a lower envelope of the events resulting in landslide initiation, although other threshold definitions exist as well (e.g., Staley et al., 2013; Ciavolella et al., 2016; Peres and Cancelliere, 2016). Obviously, ID thresholds differ greatly between climate and physiographic regions, especially in absolute values. Therefore, scaled representations have been proposed for the thresholds, such as dividing precipitation intensity by the mean annual precipitation in order to better compare the thresholds (Guzzetti et al., 2007). However, in our analysis the focus is on the unscaled measured precipitation ID representation, as it is a convenient way to compare with IDF. The exponent of most of the reported thresholds for initiation of landslides ranges between −0.2 and −0.6. For landslides triggered by short precipitation events (D≤ 1 h), the slopes of the IDF and ID curves substantially coincide (Fig. 3). On the other hand, for longer precipitation durations, ID thresholds have smaller slopes than IDF curves. This means that landslide initiation on the right side of the graph (lower precipitation intensity with longer duration) would occur with rapidly increasing return periods of precipitation events. This is counterintuitive, as during a long-lasting wet period landslides are usually more frequent, while many debris flows triggered by a very short and intense storm originate from channel bed mobilization rather than being (new) mass movements. This shows that the method used to derive ID thresholds for landslide initiation based on landslide and precipitation reports leads to troublesome interpretations. Owing to the high spatial variability of rainfall at scales smaller than 5 km (e.g., Krajewski et al., 2003; Ciach and Krajewski, 2006) and the limited density of operational rain gauge networks, the rainfall intensity observed by rain gauges systematically underestimates the actual triggering rainfall intensity at debris flow initiation locations (Marra et al., 2016), especially for short rain duration and high return period (Destro et al., 2017). This issue has been shown to significantly affect the obtained ID thresholds for debris flow initiation (Nikolopoulos et al., 2015; Marra et al., 2017). Additionally, different methods adopted to define the dry period separating rain events have been shown to strongly affect the ID threshold (e.g., Vessia et al., 2014; Melillo et al., 2015). Furthermore, several authors have already pointed out that characterizing a storm with its mean intensity, thus neglecting peaks and underestimating actual intensity, affects the estimated probability of landslide occurrence (e.g., D'Odorico et al., 2005; Peres and Cancelliere, 2016), and such an issue is obviously more significant for long storm durations. In fact, for the rainfall depth data used to derive IDF curves, the considered duration is simply a moving interval along the rainfall time series, regardless of the actual beginning and end of a rainfall event. So, the corresponding mean intensity usually refers, especially for short durations, to the heaviest part of a longer rainfall event. Conversely, whatever the criterion adopted for the definition of a rainfall event, in the case of ID threshold curves, the plotted mean intensity refers to the entire rainfall event. Thus, within very long events leading to landslide triggering, there is very likely an intensity peak, which is the “real” landslide trigger, preceded by a period of rain which contributes to predisposing the slope to failure. In the (D,I) plane, the point corresponding to the peak would be shifted to the left and upwards, compared to the point of the entire event. Given the typical slopes of IDF and ID threshold curves, this shift likely corresponds to a smaller return period.

https://www.nat-hazards-earth-syst-sci.net/18/31/2018/nhess-18-31-2018-f03

Figure 3Schematic representation of precipitation IDF curves, isolines of accumulated precipitation (ΣP) and ID threshold for shallow landslides and debris flows (simplified from Fig. 2).

Download

1.1.2 Hydrological interpretation of ID thresholds

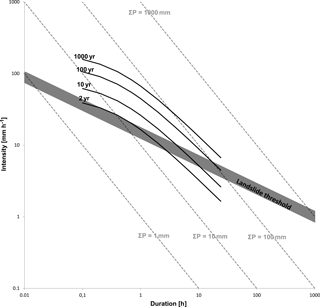
The precipitation ID thresholds are “volumetric”; i.e., every point depicts a total cumulative amount of precipitation. In Fig. 3 the global summary of ID thresholds for shallow landslides and debris flows (Guzzetti et al., 2007) is schematically represented by the dark grey area, but added to it are isolines of accumulated precipitation volume (1, 10, 100 and 1000 mm). The first observation is that the regional and global landslide thresholds clearly follow a slope different from isolines, meaning that longer-duration landslide triggering thresholds require larger water volume. This is understandable if landslides are deeper seated. However, the database contains mainly shallow landslides and debris flows (Guzzetti et al., 2007). Clearly, this indicates the role of hydrology or, to be precise, the balance between infiltration, storage and drainage capacity of a slope (Bogaard and Greco, 2015).

Many of the reported empirical precipitation thresholds range between 10 and 100 mm of accumulated precipitation. However, < 10 mm and > 1000 mm volumes needed for landslide initiation have also been reported (e.g., as summarized in Guzzetti et al., 2007). Under “normal” antecedent wetness conditions (that is, soil field capacity), an accumulated precipitation of < 10 mm is generally not capable of triggering a landslide or debris flow. Of course, such an accumulated precipitation volume can trigger a shallow landslide or debris flow in the case of nearly saturated antecedent conditions. In this latter case, the reported precipitation event is really the last “push”, the so-called trigger (see next section). On the other hand, precipitation volumes > 1000 mm and/or durations of over 100 or even 1000 h (> 1 month) are difficult to interpret in terms of average precipitation intensities and triggering thresholds for shallow landslides and debris flows. Our point here is that the current ID concept incorporates an unacceptably wide range of information with different types of hazards (debris flows and landslides related to different hydrological processes) and different temporal meteorological information (from minutes to several days). This makes the use of ID thresholds cumbersome or even misleading.

Additionally, ID thresholds have been derived by applying physically based models of infiltration and slope stability evaluation, which account for soil hydraulic properties, different initial moisture conditions and the boundary conditions through which the slope exchanges water with the surrounding hydrological system (e.g., Terlien, 1998; Rosso et al., 2006; Salciarini et al., 2006; Frattini et al., 2009; Papa et al., 2013; Peres and Cancelliere, 2014). Such physically based thresholds often do not follow Eq. (1), generally adopted for ID thresholds. For long precipitation durations, the physically based ID curves tend to flatten (e.g., Rosso et al., 2006; Salciarini et al., 2006), indicating that landslide initiation thresholds become less sensitive to (average) precipitation intensity, which is counterintuitive and a poor explanatory variable for landslide initiation.

Interestingly, Frattini et al. (2009) followed an inverse approach and obtained estimates of the probability of the precipitation characteristics leading to shallow-landslide initiation by also considering antecedent precipitation. In particular, they showed how the exponent of the IDF curves of their study area (a catchment located on the east side of Lake Como in Lombardy, northern Italy) changed from −0.65, for unconditional probability of triggering events, to −0.43, when 300 mm of rainfall in the previous 4 days was included, thus approaching the slope of the observed ID thresholds. Antecedent precipitation can be seen as an indirect means to account for the moisture conditions of the soil cover before a triggering event. Therefore, the results of Frattini et al. (2009) can also be interpreted as an indirect confirmation that considering the integral hydrological processes would improve the performance of landslide initiation thresholds.

Greco and Bogaard (2016) give an example of the possible inclusion of slope hydrological processes in the definition of landslide initiation thresholds for the case of a slope covered by loose granular volcanoclastic deposits overlying a fractured limestone bedrock. The hydraulic characteristic curves of the volcanic ashes constituting the majority of the soil cover were known (Damiano et al., 2012; Greco et al., 2013), as well as the moisture state of the cover before all 78 observed rainfall events (Comegna et al., 2016). Hence, it was possible to define non-dimensional variables by comparing the meteorological triggers with the infiltration and storage capacity of the soil cover. This non-dimensional hydro-meteorological threshold performed slightly better than the precipitation ID threshold in separating events, resulting in factors of safety smaller and greater than 1.3. The choice of referring to a factor of safety larger than 1.0 was dictated by the actually observed soil conditions during the monitoring period.

2 Trigger–cause concept: proposing hydro-meteorological landslide thresholds

Back to toptop

In the strict sense, the precipitation ID threshold is an empirical-statistical threshold drawn to separate failure and non-failure conditions based on observed landslides and precipitation records. Precipitation is described in terms of average intensity and duration. The main assumption is that there is an underlying causal relation between the recorded precipitation event and the landslide occurrence. However, by including durations up to, for instance, 1 month, the direct causal relationship is weak, and the method implicitly includes the wetness state of a region. This limitation has been recognized from the start of using ID thresholds. For several regional hazard assessment analyses, research groups have extended the ID threshold method by replacing the duration of a precipitation event on the x axis with an antecedent precipitation index or accumulated rainfall over a certain time interval (e.g., Crozier and Eyles, 1980; Glade et al., 2000; Chleoborad et al., 2006, 2008; Scheevel et al., 2017). This, however, leads to limited added information as still only precipitation information is used. However, by replacing the x axis with a direct measure or proxy for antecedent soil water content, physically relevant information is added (e.g., Crozier and Eyles, 1980; Wilson 1989; Wilson and Wieczorek, 1995; Crozier, 1999; Glade, 2000; Chirico et al., 2000; Gabet et al., 2004; Godt et al., 2006; Ponziani et al., 2012). Interestingly, by including a water balance of the potentially unstable soil, a statistical ID threshold evolves conceptually from a plot with one prevalent driver and data source (precipitation) into a plot containing two predominant drivers with two distinct timescales: the antecedent hydrological “cause” and the precipitation “trigger”. Besides soil water balance calculations, different sources of hydrological information can be used to quantify the hydrological cause of landslides. This is largely unexplored ground, partly as data availability can be cumbersome and partly because physically based, (semi-)distributed modeling was preferred.

Concerning the trigger axis, there is little debate; it is the rainfall intensity that is responsible for the short-term last push initiating a landslide. The timescale for local and regional assessment of course depends on the local situation, but hourly or daily timescales are the most common. The cause axis should represent the predisposing condition of the area under study. For hydrologically triggered landslides, it should be related to the antecedent wetness state of the area. However, there are several possible choices of hydrological variables to be plotted along the cause axis, such as (effective) soil water content, relative catchment storage and representative regional groundwater level. The choice for the trigger and cause also implies a definition of the timescale separating trigger from cause, which should be related to the characteristics of the triggered landslide but is in practice often limited by the (temporal resolution of the) available data.

As mentioned before, there are – besides the soil moisture storage calculations previously described – various examples of hydrological information added to landslide thresholds. Hashino and Murota (1971) published an analysis of landslide triggers in a catchment related to debris production using measured river discharge data to link the landslide triggers to the water balance of the catchment. They identified that the landslides in their study area occurred during above-average antecedent conditions. This is one of the earliest reported studies we know of explicitly looking at catchment water balance as an important source of information on the antecedent hydrological condition of an area in relation to landslide occurrence. Reichenbach et al. (1998) made a combined flood and landslide hazard analysis of the Tiber River catchment using 72 years of historical daily discharge data from different gauging stations where hydrological parameters were calculated, such as maximum mean daily discharge, specific discharge, and flood volume and duration. The probability of occurrence of landslides and floods was based on the ranking of the events. Combining maximum mean daily discharge and discharge intensity, regional hydrological thresholds for landslide and flood hazard (individually or combined) could be drawn. Chitu et al. (2017) followed a somewhat similar approach, analyzing the river discharge in several catchments in the Ialomita Subcarpathians in Romania for landslide events in 2014. The catchments could be characterized as having low/high relative storage. Additionally, a calibrated regional rainfall-runoff model was used for hydrological analysis of landslides in specific catchments. Detailed analysis of the (modeled) hydrological response indicated that in two catchments with low infiltration capacity the direct runoff was strongly related to landslide occurrence, whereas it could be linked to modeled soil infiltration flux in another catchment. Extending the above to deep-seated landslides, the connected regional groundwater level could be informative. Bogaard et al. (2013) studied the hydro-meteorological triggering threshold of the re-activating coastal Villerville–Cricqueboeuf landslide, Normandy, France. In this situation the hinterland of the coastal cliff consists of a well-defined regional groundwater level. Landslide reactivation was seen to take place only when water level was in the upper, more permeable top layer. The triggering rain event together with surpassing a certain regional groundwater threshold could explain three of the four reactivations. Note that these groundwater levels were not taken in the active landslide area but several kilometers inland.

Recently, further attempts have been made to use river discharge and lumped water storage in a catchment as a proxy for the predisposing conditions for landslides along its slopes. Following Hashino and Murota (1971), the basic idea is that when “more-than-average” water is stored in the catchment it is more likely that a rainfall event will trigger landslides. The disadvantage of using catchment-wide storage is the relatively low spatial resolution and the difficulty of having (reliable and homogeneous) discharge time series in catchments. Moreover, catchment storage assessment necessitates information on evaporation, which can have significant uncertainties. Of course, such an approach works only if the causes of the predisposing conditions for landslides are somewhat related to catchment scale hydrological processes. Ciavolella et al. (2016) defined a cause–trigger hydro-meteorological threshold in the catchment of the river Scoltenna in Emilia-Romagna (Italy), linking catchment storage and event rainfall intensity, and compared its performance with that of a statistical ID precipitation threshold. The two thresholds performed similarly, with the hydro-meteorological thresholds being more accurate for identifying landslides but giving a somewhat larger number of false positives.

These examples indicate that considering hydrological causes could be useful for a better identification of landslide initiation, but, at the same time, they show that the correct identification of the hydrological processes involved in the establishment of the predisposing conditions for landslides is mandatory for choosing the most informative hydrological variable to be plotted along the x cause axis.

3 Concluding remarks and outlook

Back to toptop

The intrinsic limitations of precipitation ID thresholds for the identification of landslide initiation conditions have been noted for some time. Indeed, such thresholds neglect the role of the hydrological processes occurring along slopes, which predispose hillslopes to failure (causes), and focus predominately on the characteristics of the last rainfall events leading to slope failure (triggers). As a consequence, the predictive accuracy of the ID thresholds is often low, even when they refer to small areas. We argue that the threshold values for rainfall intensity of short and long duration (the far left and right side of the graphs, respectively) have limited physical meaning and, consequently, that the use of precipitation ID thresholds can lead to misleading interpretations of initiation conditions, as important antecedent conditions and rainfall intensity variations are not taken into account. For this reason, we here advocate being very careful in uncritically using the precipitation ID thresholds as a kind of regional characteristic of (shallow-)landslide occurrence.

Equally, for this and several other reasons, many colleagues advocate the use of spatially distributed physically based models for assessing landslide probability. The obvious downside is that large data input and a well-calibrated model are required. However, it is fair to say that data are becoming more and more available, and even precipitation predictions are improving rapidly, especially with short lead time. The use of high-quality rainfall prediction with very short lead time (e.g., 3 h) requires efficient numerical models combined with high computational power, especially if predictions are used for early-warning purposes. This, in practice, is still easier said than done. Therefore, we believe that lumped, empirical (or semi-empirical) thresholds will continue having a practical value, which still justifies scientific attention.

We propose to use the cause–trigger concept for defining regional landslide initiation thresholds. This, we agree, is challenging but, in our opinion, not impossible. First of all, it is necessary to define the characteristic timescale separating the (dynamic) long-term predisposing hydrological cause from the short “final” landslide hazard triggering. This obviously depends on the landslide type and physiographic characteristics. Looking at the discussed examples, it becomes clear that the choice of the most informative hydrological variable to be used as a proxy for predisposing landslide conditions strictly depends on site-specific geomorphological characteristics and that accurate analysis of the boundaries through which the potentially unstable area exchanges water with the surrounding hydrological systems is mandatory. In other words, for the assessment of predisposing landslide conditions, the water balance of the slope should be assessed, but getting information on the inherent hydrological processes (e.g., evaporation, runoff, groundwater recharge) at the required spatial-temporal resolution is often a challenge and could require some kind of calculations or modeling. However, rapidly more and higher-resolution hydrological data are becoming available which can be used in assessing predisposing hydrological conditions.

Data availability

Back to toptop

Data availability.

Data used for Fig. 1 can be found in Wenzel (1982), Iida (2004), Rossi and Villani (1994), Brutsaert (2005), Elsebaie (2012), Chang et al. (2015), Rasel and Hossain (2015), Van de Vyver (2015) and Damé et al. (2016). Data used for Fig. 2 can be found in Guzzetti et al. (2007).

Competing interests

Back to toptop

Competing interests.

The authors declare that they have no conflict of interest.

Acknowledgements

Back to toptop

Acknowledgements.

This invited perspectives paper was motivated based on frequent discussions with many colleagues working in the field of landslide hazard assessment. We are grateful to them all. Also the excellent reviews by one anonymous reviewer, Roy C. Sidle, Francesco Marra, and Ben Mirus and his colleagues from USGS are greatly acknowledged. We thank them for pointing to omissions and the many insightful comments which considerably improved the paper.

Edited by: Heidi Kreibich
Reviewed by: Roy C. Sidle and one anonymous referee

References

Back to toptop

Anagnostopoulos, G. G., Fatichi, S., and Burlando, P.: An advanced process-based distributed model for the investigation of rainfall-induced landslides: The effect of process representation and boundary conditions, Water Resour. Res., 51, 7501–7523, https://doi.org/10.1002/2015WR016909, 2015.

Anderson, M. G. and Lloyd, D. M.: Using a combined hydrology stability model to develop cut slope design charts, P. I. Civil. Eng., 91, 705–718, https://doi.org/10.1680/iicep.1991.17486, 1991.

Aristizábal, E., Ignacio Vélez, J., Martínez, H. E., and Jaboyedoff, M.: SHIA_Landslide: a distributed conceptual and physically based model to forecast the temporal and spatial occurrence of shallow landslides triggered by rainfall in tropical and mountainous basins, Landslides, 13, 497–517, https://doi.org/10.1007/s10346-015-0580-7, 2016.

Arnone, E., Noto, L. V., Lepore, C., and Bras, R. L.: Physically-based and distributed approach to analyze rainfall-triggered landslides at watershed scale, Geomorphology, 133, 121–131, 2011.

Baum, R. L. and Godt, J. W.: Early warning of rainfall-induced shallow landslides and debris flows in the USA, Landslides, 7, 259–272, https://doi.org/10.1007/s10346-009-0177-0, 2010.

Baum, R. L., Savage, W. Z., and Godt, J. W.: TRIGRS – A FORTRAN program for transient rainfall infiltration and grid-based regional slope-stability analysis, version 2.0. US Geological Survey Open-File Rep 2008-1159, available at: http://pubs.er.usgs.gov/publication/ofr20081159 (last access: 21 December 2017), 2008.

Bernard, M. M.: Formulas for rainfall intensities of long duration, T. Am. Soc. Civ. Eng., 96, 592–606, 1932.

Berti, M., Martina, M. L. V., Franceschini, S., Pignone, S., Simoni, A., and Pizziolo, M.: Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach, J. Geophys. Res., 117, F04006, https://doi.org/10.1029/2012JF002367, 2012.

Bogaard, T. A., Maharjan, L. D., Maquaire, O., Lissak, C., and Malet, J.-P.: Identification of hydro-meteorological triggers for Villerville coastal landslide, Vol. 5 of Landslide Science and Practice, edited by: Margottini, C., Canuti, P, and Sassa, K., 141–145 ISBN: 978-3-642-31309-7 (Print) 978-3-642-31310-3 (Online), Springer, Berlin Proceedings of the Second World Landslide Forum, 3–7 October 2011, Rome, Italy, 2013.

Bogaard, T. A. and Greco R.: Landslide hydrology: from hydrology to pore pressure, WIREs Water, 3, 439–459, https://doi.org/10.1002/wat2.1126, 2015.

Borga, M., Dalla Fontana, G., Da Ros, D., and Machi, D. L.: Shallow landslide hazard assessment using a physically based model and digital elevation data, Environ. Geol., 35, 81–88, https://doi.org/10.1007/s002540050295, 1998.

Brutsaert, W.: Hydrology – An introduction, Cambridge Univ. Press, Cambridge, UK, 2005.

Burton, A. and Bathurst, J.: Physically based modelling of shallow landslide sediment yield at a catchment scale. Environ. Geol., 35, 89–99, https://doi.org/10.1007/s002540050296, 1998.

Caine, N: The rainfall intensity: duration control of shallow landslides and debris flows, Geogr. Ann. A, 62, 23–27, 1980.

Chacón, J., Irigaray, C., Fernández, T., and El Hamdouni, R.: Engineering geology maps: landslides and geographical information systems, B. Eng. Geol. Environ., 65, 341–411, https://doi.org/10.1007/s10064-006-0064-z, 2006.

Chang, K. B., Lai, S. H., and Othman, F.: Comparison of Annual Maximum and Partial Duration Series for Derivation of Rainfall Intensity-Duration-Frequency Relationships in Peninsular Malaysia, J. Hydrol. Eng., 21, 05015013, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001262, 2015.

Chirico, G. B., Claps, P., Rossi, F., and Villani, P.: Hydrological condition leading to debris-flow initiation in the Campanian volcanoclastic soils, in: Mediterranean Storms: proceedings of the EGS Plinius conference, Maratea, Italy, edited by: Claps, P. and Siccardi, F., October 1999, 473–484, Editoriale Bios, Cosenza, Italy, 2000.

Chitu, Z., Bogaard, T. A., Busuioc, A., Burcea, S., Sandric, I., and Adler, M.-J.: Identifying hydrological pre-conditions and rainfall triggers of slope failures at catchment scale for 2014 storm events in the Ialomita Subcarpathians, Romania, Landslides, 14, 419–434, https://doi.org/10.1007/s10346-016-0740-4, 2017.

Chleborad, A. F., Baum, R. L., and Godt, J. W.: Rainfall Thresholds for Forecasting Landslides in the Seattle, Washington, Area – Exceedance and Probability, Geological Survey Open-File Report 2006–1064, available at: http://pubs.er.usgs.gov/publication/ofr20061064 (last access: 21 December 2017), 2006.

Chleborad, A. F., Baum, R. L., Godt, J. W., and Powers, P. S.: A prototype for forecasting landslides in the Seattle, Washington, Area, Reviews in Engineering Geology, 20, 103–120, https://doi.org/10.1130/2008.4020(06), 2008.

Chow, V. T., Maidment, D. R., and Mays, L. W.: Applied Hydrology, McGraw-Hill Publishing Company, Singapore, ISBN: 0071001743, 1988.

Ciach, G. J. and Krajewski, W. F.: Analysis and modeling of spatial correlation structure in small-scale rainfall in Central Oklahoma, Adv. Water Res., 29, 1450–1463, https://doi.org/10.1016/j.advwatres.2005.11.003, 2006.

Ciavolella, M., Bogaard, T. A., Gargano, R., and Greco, R.: Is there predictive power in hydrological catchment information for regional landslide hazard assessment?, Proced. Earth Plan. Sc., 16, 195–203, https://doi.org/10.1016/j.proeps.2016.10.021, 2016.

Comegna, L., Damiano, E., Greco, R., Guida, A., Olivares, L., and Picarelli, L.: Field hydrological monitoring of a sloping shallow pyroclastic deposit, Can. Geotech. J., 53, 1125–1137, https://doi.org/10.1139/cgj-2015-0344, 2016.

Crozier, M. J.: Prediction of rainfall-triggered landslides: a test of the antecedent water status model, ESPL, 24, 825–833, 1999.

Crozier, M. J. and Eyles, R. J.: Assessing the probability of rapid mass movement, Proceedings of the Third Australia-New Zealand Conference on Geomechanics, New Zealand Institute of Engineers, Proceedings of Technical Groups, 6, 47–53, 1980.

Damé, R. de C. F., Teixeira-Gandra, C. F. A., Guedes, H. A. S., da Silva, G. M., and da Silveira, S. C. R.: Intensity–Duration–Frequency relationships: stochastic modeling and disaggregation of daily rainfall in the lagoa Mirim watershed, Rio Grande do Sul, Brazil, Eng. Agric., 36, 492–502, https://doi.org/10.1590/1809-4430-Eng.Agric.v36n3p492-502/2016, 2016.

Damiano, E., Olivares, L., and Picarelli, L.: Steep-slope monitoring in unsaturated pyroclastic soils, Eng. Geol. 137–138, 1–12, 2012.

Destro, E., Marra F., Nikolopoulos, E. I., Zoccatelli, D. Creutin, J. D., and Borga, M.: Spatial estimation of debris flows-triggering rainfall and its dependence on rainfall return period, Geomorphology, 278, 269–279, https://doi.org/10.1016/j.geomorph.2016.11.019, 2017.

D'Odorico, P., Fagherazzi, S., and Rigon, R.: Potential for landsliding: Dependence on hyetograph characteristics, J. Geophys. Res., 110, F01007, https://doi.org/10.1029/2004JF000127, 2005.

Elsebaie, I. H.: Developing rainfall intensity–duration–frequency relationship for two regions in Saudi Arabia, Journal of King Saud University-Engineering Sciences, 24, 131–140, 2012.

Fan, L., Lehmann, P., and Or, D.: Effects of Soil Spatial Variability at the Hillslope and Catchment Scales on Characteristics of Rainfall-Induced Landslides, Water Resour. Res., 52, 1781–1799, https://doi.org/10.1002/2015WR017758, 2016.

Frattini, P., Crosta, G. B., Fusi, N., and Dal Negro, P.: Shallow landslides in pyroclastic soils: a distributed modelling approach for hazard assessment, Eng. Geol., 73, 277–295, 2004.

Frattini, P., Crosta, G., and Sosio, R.: Approaches for defining thresholds and return periods for rainfall-triggered shallow landslides, Hydrol. Process. 23, 1444–1460, https://doi.org/10.1002/hyp.7269, 2009.

Gabet, E. J., Burbank, D. W., Putkonen, J. K., Pratt-Sitaula, B. A., and Ojha, T.: Rainfall thresholds for landsliding in the Himalayas of Nepal, Geomorphology 63, 131–143, https://doi.org/10.1016/j.geomorph.2004.03.011, 2004.

Glade, T.: Modelling landslide-triggering rainfalls in different regions in New Zealand – the soil water status model, Z. Geomorphol., 122, 63–84, 2000.

Glade, T., Crozier, M., Smith, P.: Applying probability determination to refine landslide-triggering rainfall thresholds using an empirical “ antecedent daily rainfall model”, Pure and Appl. Geophys., 157, 1059–1079, 2000.

Godt, J. W., Baum, R. L., and Chleborad, A. F.: Rainfall characteristics for shallow landsliding in Seattle, Washington, USA, Earth Surf. Proc. Land., 31, 97–110, https://doi.org/10.1002/esp.1237, 2006.

Greco, R. and Bogaard, T. A.: The influence of non-linear hydraulic behavior of slope soil covers on rainfall intensity-duration thresholds. Landslides and Engineered Slopes. Experience, Theory and Practice – edited by: Aversa, S., Cascini, L., Picarelli, L., and Scavia, C., © 2016 Associazione Geotecnica Italiana, Rome, Italy, ISBN 978-1-138-02988-0, 2016.

Greco, R., Comegna, L., Damiano, E., Guida, A., Olivares, L., and Picarelli, L.: Hydrological modelling of a slope covered with shallow pyroclastic deposits from field monitoring data, Hydrol. Earth Syst. Sci., 17, 4001–4013, https://doi.org/10.5194/hess-17-4001-2013, 2013.

Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P.: Rainfall thresholds for the initiation of landslides in central and southern Europe, Meteorol. Atmos. Phys., 98, 239–267, 2007.

Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P.: The rainfall intensity-duration control of shallow landslides and debris flows: an update, Landslides, 5, 3–17, 2008.

Hashino, M. and Murota, A.: A stochastic study on debris production in the form of landslide due to heavy rainfall. Proceedings of the Japan Society of Civil Engineers, No. 188, 33–43, https://doi.org/10.2208/jscej1969.1971.188_33, 1971.

Iida, T.: Theoretical research on the relationship between return period of rainfall and shallow landslides, Hydrol. Process, 18, 739–756, https://doi.org/10.1002/hyp.1264, 2004.

Koutsoyiannis, D., Demosthenes, K., and Manetas, A.: A Mathematical Framework for Studying the Rainfall Intensity-Duration-Frequency Relationships, J. Hydrol., 303, 215–230, 1998.

Krajewski, W. F., Ciach G. J., and Habib, E.: An analysis of small-scale rainfall variability in different climatic regimes, Hydrol. Sci. J., 48, 151–162, https://doi.org/10.1623/hysj.48.2.151.44694, 2003.

Lepore, C., Arnone, E., Noto, L. V., Sivandran, G., and Bras, R. L.: Physically based modeling of rainfall-triggered landslides: a case study in the Luquillo forest, Puerto Rico, Hydrol. Earth Syst. Sci., 17, 3371–3387, https://doi.org/10.5194/hess-17-3371-2013, 2013.

Marra, F., Nikolopoulos, E. I., Creutin, J. D., and Borga, M.: Space–time organization of debris flows-triggering rainfall and its effect on the identification of the rainfall threshold relationship, J. Hydrol., 541, 246–255, https://doi.org/10.1016/j.jhydrol.2015.10.010, 2016.

Marra, F., Destro, E., Nikolopoulos, E. I., Zoccatelli, D., Creutin, J. D., Guzzetti, F., and Borga, M.: Impact of rainfall spatial aggregation on the identification of debris flow occurrence thresholds, Hydrol. Earth Syst. Sci., 21, 4525–4532, https://doi.org/10.5194/hess-21-4525-2017, 2017.

Melillo, M., Brunetti, M. T., Peruccacci, S., Gariano, S. L. and Guzzetti, F.: An algorithmfor the objective reconstruction of rainfall events responsible for landslides, Landslides, 12, 311–320, https://doi.org/10.1007/s10346-014-0471-3, 2015.

Montgomery, D. R. and Dietrich, W. E.: A physically based modelfor the topographic control on shallow landsliding, Water Resour. Res., 30, 1153–1171, 1994.

Napolitano, E., Fusco, F. Baum, R. L., Godt, J. W., and De Vita, P.: Effect of antecedent hydrological conditions on rainfall triggering of debris flows in ash-fall pyroclastic mantled slopes of Campania (southern Italy), Landslides, 13, 967–983, https://doi.org/10.1007/s10346-015-0647-5, 2015.

Nikolopoulos, E. I., Borga, M., Creutin, J. D., and Marra, F.: Estimation of debris flow triggering rainfall: Influence of rain gauge density and interpolation methods, Geomorphology, 243, 40–50, https://doi.org/10.1016/j.geomorph.2015.04.028, 2015.

Pack, R. T., Tarboton, D. G., and Goodwin, C. N.: The SINMAP approach to terrain stability mapping, 8th congress of the international association of engineering geology, 21–25 September 1988, Vancouver, British Columbia, Canada, Vol. 21, 1998.

Papa, M. N., Medina, V., Ciervo, F., and Bateman, A.: Derivation of critical rainfall thresholds for shallow landslides as a tool for debris flow early warning systems, Hydrol. Earth Syst. Sci., 17, 4095–4107, https://doi.org/10.5194/hess-17-4095-2013, 2013.

Peres, D. J. and Cancelliere, A.: Derivation and evaluation of landslide-triggering thresholds by a Monte Carlo approach, Hydrol. Earth Syst. Sci., 18, 4913–4931, https://doi.org/10.5194/hess-18-4913-2014, 2014.

Peres, D. J. and Cancelliere, A.: Estimating return period of landslide triggering by Monte Carlo simulation. J. Hydrol., 241, 256–271, https://doi.org/10.1016/j.jhydrol.2016.03.036, 2016.

Peruccacci, S., Brunetti, M. T., Gariano, S. L., Melillo, M., Rossi, M., and Guzzetti, F.: Rainfall thresholds for possible landslide occurrence in Italy, Geomorphology, 290, 39–57, https://doi.org/10.1016/j.geomorph.2017.03.031, 2017.

Ponziani, F., Pandolfo, C., Stelluti, M., Berni, N., Brocca, L., and Moramarco, T.: Assessment of rainfall thresholds and soil moisture modelling for operational hydrogeological risk prevention in Umbria region (central Italy), Landslides, 9, 229–237, https://doi.org/10.1007/s10346-011-0287-3, 2012.

Rasel, M. M. and Hossain, S. M.: Development of rainfall intensity duration frequency (R-IDF) equations and curves for seven divisions in Bangladesh, International Journal of Scientific & Engineering Research, 6, 96–101, 2015.

Reichenbach, P., Cardinali, M., De Vita, P., and Guzzetti, F.: Regional hydrological thresholds for landslides and floods in the Tiber River Basin (central Italy), Environ. Geol., 35, 146–159, https://doi.org/10.1007/s002540050301, 1998.

Rossi, F. and Villani, P.: Regional flood estimation methods, in: Coping with Floods, edited by: Rossi G., Harmancioǧlu, N., and Yevjevich V., NATO ASI Series (Series E: Applied Sciences), Vol. 257, Springer, Dordrecht, the Netherlands, 1994.

Rossi, M., Luciani, S., Valigi, D., Kirschbaum, D., Brunetti, M. T., Peruccacci, S., and Guzzetti, F.: Statistical approaches for the definition of landslide rainfall thresholds and their uncertainty using rain gauge and satellite data, Geomorphology, 285, 16–27, https://doi.org/10.1016/j.geomorph.2017.02.001, 2017.

Rosso, R., Rulli, M. C., and Vannucchi, G.: A physically based model for the hydrologic control on shallow landsliding, Water Resour. Res., 42, W06410, https://doi.org/10.1029/2005WR004369, 2006.

Salciarini, D., Godt, J. W., Savage, W. Z., Conversini, P., Baum, R. L., and Michael, J. A.: Modeling regional initiation of rainfall-induced shallow landslides in the eastern Umbria Region of central Italy, Landslides, 3, 181–194, 2006.

Scheevel, C. R., Baum, R. L., Mirus, B. B., Smith, J. B.: Precipitation thresholds for landslide occurrence near Seattle, Mukilteo, and Everett, Washington: U.S. Geological Survey Open-File Report 2017–1039, https://doi.org/10.3133/ofr20171039, 2017.

Sidle, R. C. and Ochiai, H.: Landslides: Processes, Prediction, and Land Use. Am. Geophys. Union Water Resour. Monogr, Vol. 18, American Geophysical Union, Washington, D.C., 312 pp., 2006.

Staley, D. M., Kean, J. W. Cannon, S. H., Schmidt, K. M., and Laber, J. L.: Objective definition of rainfall intensity – duration thresholds for the initiation of post-fire debris flows in southern California, Landslides, 10, 547–562, https://doi.org/10.1007/s10346-012-0341-9, 2013.

Terlien, M. T. J.: The determination of statistical and deterministic hydrological landslide-triggering thresholds, Environ. Geol., 35, 1240–130, 1998.

Van Beek, L. P. H.: Assessment of the influence of changes in climate and land use on landslide activity in a Mediterranean environment, Doctoral Thesis, Netherlands Geographical Studies 294, Utrecht, the Netherlands, 2002.

Van de Vyver, H.: Bayesian estimation of rainfall intensity–duration–frequency relationships, J. Hydrol. 529, 1451–1463, 2015.

Vessia, G., Parise, M., Brunetti, M. T., Peruccacci, S., Rossi, M., Vennari, C., and Guzzetti, F.: Automated reconstruction of rainfall events responsible for shallow landslides, Nat. Hazards Earth Syst. Sci., 14, 2399–2408, https://doi.org/10.5194/nhess-14-2399-2014, 2014.

von Ruette, J., Lehmann, P., and Or, D.: Rainfall-triggered shallow landslides at catchment scale: Threshold mechanics-based modeling for abruptness and localization, Water Resour. Res., 49, 6266–6285, https://doi.org/10.1002/wrcr.20418, 2013.

Wenzel, H. G.: Rainfall for Urban Stormwater Design, in: Urban Storm Water Hydrology, edited by: Kibler, D. F., Washington, D.C., Water Resources Monograph, 7, AGU, 1982.

Wieczorek, G. F. and Glade, T.: Climatic factors influencing occurrence of debris flows, in: Debris-flow hazards and related phenomena, edited by: Jakob, M. and Hungr, O., Praxis and Springer, Berlin Heidelberg New York, 325–362, 2005.

Wilson, R. C.: Rainstorms, pore pressure and debris flows: a theoretical framework, in: Landslides in semi-arid environment, edited by: Sadler, P. M. and Morton, D. M., pub. no. 2, 101–117, Inland Geological Society, Riverside, USA, 1989.

Wilson, R. C. and Wieczorek, G. F.: Rainfall thresholds for the initiation of debris flows at La Honda, California, Environ. Eng. Geosci., 1, 11–27, 1995.

Wu, W. and Sidle, R. C.: A distributed slope stability model for steep forested basins, Water Resour. Res., 31, 2097–2110, 1995.