the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Statistical theory of probabilistic hazard maps: a probability distribution for the hazard boundary location
Andrea Bevilacqua
Marcus I. Bursik
The study of volcanic flow hazards in a probabilistic framework centers around systematic experimental numerical modeling of the hazardous phenomenon and the subsequent generation and interpretation of a probabilistic hazard map (PHM). For a given volcanic flow (e.g., lava flow, lahar, pyroclastic flow, ash cloud), the PHM is typically interpreted as the point-wise probability of inundation by flow material.
In the current work, we present new methods for calculating spatial representations of the mean, standard deviation, median, and modal locations of the hazard's boundary as ensembles of many deterministic runs of a physical model. By formalizing its generation and properties, we show that a PHM may be used to construct these statistical measures of the hazard boundary which have been unrecognized in previous probabilistic hazard analyses. Our formalism shows that a typical PHM for a volcanic flow not only gives the point-wise inundation probability, but also represents a set of cumulative distribution functions for the location of the inundation boundary with a corresponding set of probability density functions. These distributions run over curves of steepest probability gradient ascent on the PHM. Consequently, 2-D space curves can be constructed on the map which represents the mean, median, and modal locations of the likely inundation boundary. These curves give well-defined answers to the question of the likely boundary location of the area impacted by the hazard. Additionally, methods of calculation for higher moments including the standard deviation are presented, which take the form of map regions surrounding the mean boundary location. These measures of central tendency and variance add significant value to spatial probabilistic hazard analyses, giving a new statistical description of the probability distributions underlying PHMs.
The theory presented here may be used to aid construction of improved hazard maps, which could prove useful for planning and emergency management purposes. This formalism also allows for application to simplified processes describable by analytic solutions. In that context, the connection between the PHM, its moments, and the underlying parameter variation is explicit, allowing for better source parameter estimation from natural data, yielding insights about natural controls on those parameters.
The probabilistic study of volcanic hazards is part of an emerging paradigm in physical volcanology, one that openly admits and seeks to calculate and characterize the uncertainty inherent to physical modeling of hazardous volcanic processes (Bursik et al., 2012; Connor et al., 2015; Bevilacqua, 2016; Sandri et al., 2016). Critically, this approach is founded on the notion that physical parameters related to these processes can be represented by a probability distribution. The distribution is propagated by a physical model to yield a space of hazard distributions which put probabilistic constraints on quantities that would be fixed in a deterministic, scenario-based modeling framework. In practice this has typically been accomplished by accumulating the statistics of the processes through deterministic modeling over an ensemble of model inputs (Neri et al., 2015; Biass et al., 2016; Tierz et al., 2016; Bevilacqua et al., 2017; Gallant et al., 2018; Patra et al., 2018b). Polynomial chaos approximations and Gaussian model surrogates can provide fast algorithms to obtain these statistics (Bursik et al., 2012; Madankan et al., 2012; Stefanescu et al., 2012; Spiller et al., 2014; Bayarri et al., 2015; Tierz et al., 2018). Owing to the nature of the studied processes, the results are typically displayed in map form and contain a large amount of spatial information, the interpretation of which has become a source of extensive study (Calder et al., 2015; Thompson et al., 2015). Because the information in these maps is potentially of great interest to a wide community of stakeholders including governments, planners, emergency managers, local residents, and others spanning a wide range of familiarity with probabilistic reasoning, finding the best approach to condensing these data-rich maps is nontrivial. The raw probabilities are considered less useful to many end users despite their significant information content (Thompson et al., 2015). Often the information in these maps is presented qualitatively as high, medium, and low hazard or simply high and low hazard (Calder et al., 2015; Wagner et al., 2015). The reduction of a complex probability distribution to a relative categorization as in a high–low hazard scheme generally involves significant nuance in blending scientific information, decision-making, and administrative considerations. In the scientific component of the analysis, such a categorization could be based on a probability threshold, in many cases a certain percentile of the distribution, which corresponds to a probability contour on the map. While this is the most obvious method it is just one of many options for declaring this categorical boundary.
At present, a probabilistic hazard map (PHM) for a given hazard is easily constructed from numerical modeling; however, its most commonly used statistical product in hazard communication is just the set of probability contours. Consequently if a binary volcanic hazard map were to be constructed from a PHM showing the region of no likely impact versus the region of likely impact, the analyst would have to decide where to draw the line: possibly at the 5 % probability contour (a safe, conservative choice), the median contour (50 %) (a good estimate for the most likely impact–no-impact boundary), or some other choice of percentile. Often the choice of the contour level is based on agreements or official protocols made by civil protection authorities. Such potentially high-consequence decisions would benefit from additional statistical analyses which generate other tools for this task. For example, it may be useful to know the average geographical limits of a particular hazard in addition to the point-wise probability of hazard impact. For any sample data set or theoretical probability distribution, the mean and variance as well as one or more modal values are calculable in addition to the median and other percentiles. An important deficiency in the analysis of the PHM is that, previously, scientific estimates of the likely hazard boundary (a single curve on the map) have lacked the formal framework required for unique determination of statistical estimates such as the mean, variance, and higher moments of the distribution of hazard boundary locations.
For any given volcanic hazard analysis which maps probabilities of a given event, the probability values may represent a wide array of concepts in probability theory including cumulative probabilities, probability densities, conditional probabilities, and others. Here, the point-wise probability is interpreted as the relative frequency of hazard impact as predicted by repeated simulation using a deterministic physical model or ensemble of models equipped with an ensemble of inputs spanning the realistic range of underlying uncertain parameters. In the following theory and analysis, we only consider spatial probability distributions which map the probability of a given hazard impacting a given location where there is at least one point in space with a modeled probability of unity. Although this excludes the study of many possible PHMs, it covers a sufficiently wide range of models which are regular or regularized and span a realistically limited subspace of the general parameter space; that is, they depend continuously on the inputs or, in this case, maintain some level of spatial correlation across a realistically narrow, continuous range of inputs. In general, the methods detailed here are agnostic with respect to the type of uncertainty which is modeled. For any probabilistic geophysical model, there exist epistemic and aleatory uncertainties. The division between aleatory uncertainty and epistemic uncertainty corresponds to the distinction between intrinsic randomness of the system and the additional uncertainty that affects its representation, the latter originating from incomplete information about the underlying physical processes. Clearly PHMs constructed purely from aleatory uncertainties in the inputs have the most concrete meanings. However, PHMs constructed from a mix of aleatory and epistemic uncertainties can be considered as a single member of a time-dependent sequence of such assessments, each of which captures the types of uncertainty encoded in the generation of the PHM that is understood at that time. In general, as epistemic uncertainty decreases over time, the later assessments will become more accurate. As long as the uncertainties can be described as a probability space, these analyses hold up to current geophysical knowledge. Although varying the parameters in a single model gives the most concrete meaning, these methods could be applied to PHMs constructed from an ensemble of models provided that the ensemble shows regular behavior. Here, we focus on analyses of single hazards, although the boundary-finding methods could be justified to analyze PHMs constructed for multiple hazards.
Throughout this work, we realize these methods with examples using geophysical mass flow (GMF) models of inundation hazards. This is done primarily because the flow boundary is easily definable and conceptualized in these models, giving a consistent intuition to the complicated mathematical quantities discussed here. However, these concepts extend to many other types of hazard models where a particular threshold is of interest in defining the region impacted by a hazard in volcanology and other fields including concentration thresholds in volcanic clouds (Bursik et al., 2012), thickness thresholds in tephra fallout (Sandri et al., 2016), ballistic ejecta impact count thresholds (Biass et al., 2016), pyroclastic density current invasion (Bevilacqua et al., 2017), lava flow inundation (Gallant et al., 2018), tsunami run-up thresholds (Geist and Parsons, 2006; Grezio et al., 2017), ground-shaking thresholds in seismic hazards (Kvaerna et al., 1999), hurricane wind speed thresholds (Splitt et al., 2014), and many others. All of these examples can be cast in the same mathematical formulation that we detail below. A full evaluation of suitable and unsuitable types of probabilistic hazard assessments is beyond the scope of this work.
The work of Stefanescu et al. (2012) provided a rigorous framework for calculating the PHM from a Gaussian emulator of GMF simulations. Within that framework, the PHM is the point-wise mean probability of hazard impact, and the uncertainty bounds for that probability are well-defined. Although this method is robust, it has not been applied in many hazard studies. Furthermore, as with most calculations of PHMs, the interval 0 < Prob(Hazard Impact) < 1 occupies a very large region of space. As in the above hypothetical binary hazard-mapping scenario, the question remains – from the perspective of a probabilistic volcanic hazard analysis, where is the likely boundary of the impacted area?
The goal of the present work is to extend the probability theory of PHMs to construct statistically meaningful answers to this question. To this end, we give an explicit mathematical definition of the PHM, defining explicitly the connection between the cumulative exceedance probabilities and probability densities in a PHM and estimates of the likely hazard boundary. More specifically, we calculate spatial representations of the PHM's moments including the mean and variance of the hazard boundary location as well as its modality. We stipulate that the methods detailed here apply only to the scientific analysis component of any hazard-mapping project and must be considered as just one piece of the hazard-map-making process. This effort combines mathematical tools and concepts from probability theory, the study of dynamical systems, and differential geometry.
Solutions to flow models which involve depth-integrated partial differential equations (e.g., Saint-Venant-type shallow water equations) typically include solving for the distribution of flow thicknesses over position and parameter space:
where x is the position vector and β∈ℬ is an n vector in parameter space ℬ; that is, if there are n input parameters to a model, ℬ⊂ℝn. The parameter space ℬ is taken as a probability space; however, we discuss it here only in a simplified sense without reference to sigma-algebras. For the present purposes, we note only that ℬ contains all values of the input parameters that may be considered reasonable or feasible for the application. The notation h(x;β) has been used to indicate that the model output is a function of position x that depends upon the input parameters in β. For any choice of model, the vector β is simply a collection of the input parameters to the model. From the solutions h(x;β), an indicator function can be constructed to denote the region in space, Ω(β), where the solution space has been inundated:
where h0 is the inundation thickness threshold of interest. For many GMFs including lahars, lava flows, and pyroclastic density currents, the threshold of interest is h0=0 since any amount of inundation is a significant hazard; however, in the typical practice of PHM construction from numerical modeling, a nonzero thickness tolerance is typically set due to inaccuracies in the solver near free boundaries (h(x)=0) or other considerations (e.g., Patra et al., 2018b). Although doing so is inaccurate for the flows considered in this work, a sufficiently small threshold captures the essential features of the flow boundary. In assessments of other types of hazards with nonzero thresholds of interest (e.g. tephra fallout required for collapse of a particular roofing material), the true threshold may be used without introducing problems due to these solver inaccuracies.
2.1 Probabilistic hazard map
The construction of any PHM requires the definition of a joint probability distribution of the inputs given by a probability density function (PDF) which measures the parameter space ℬ. In general, the choice of probability distribution for β will represent a combination of aleatory and epistemic uncertainties. Consequently, calculating the PHM amounts to propagating f(β) from parameter space (ℬ) through a physical model into Euclidean space. The PHM is then calculated by integration through all of the parameter space:
In the integral, the indicator function acts as a filter, removing parameter space points from the integral which do not yield solutions exceeding the threshold at a given space point. In spatial subsets where all values of β in the support of f give solutions which exceed the threshold, the indicator is identically unity and ϕ=1 by the scaling condition for a valid PDF f(β). Consequently, globally and measures the probability of finding material in the simulated flow at position x. An alternative interpretation is the following: any given location exists in a binary state, either impacted or not impacted by the flow, which is represented spatially by an indicator function with the model acting as a mapping from a set of inputs β to the indicator 1Ω(β)(x). Invoking the law of the unconscious statistician (LOTUS) (DeGroot and Schervish, 2012), the PHM is then a formula for computing the probability of being in either member of the binary state at each point, since the indicator function (model output) is integrated against the PDF for the model inputs. This second interpretation (using the LOTUS) is the result of encoding the binary state as a statement of certainty (probability zero or unity) that a given point is inundated in each model output.
If the range of realistic parameter values were confined to a single point β0 in parameter space, then the parameter PDF f is the Dirac delta function δ(β−β0), resulting in a PHM which is merely the indicator function: . This is also the result for a PHM constructed for a single deterministic run of the model. This corresponds to the intuition that complete certainty of input parameters corresponds with complete certainty of the spatial extent of the hazard (the region where ϕ=1).
If the parameter space is measured by a uniform distribution (maximal entropy distribution), the probabilistic hazard map (PHM) is constructed by mean value integration of the indicator function through the parameter space:
where the symbol ∫ℬ is the mean value integral. This approach is a good assumption in hazard analysis if there is no a priori knowledge of the uncertain parameters except for reasonable bounds.
In the context of a typical probabilistic hazard modeling effort, the solution space and parameter space are discrete with a uniform distribution in parameter space, and these steps are accomplished merely by cell-wise averaging of the indicator functions derived from each model run to generate a discretized 2-D hazard map ϕ=ϕij. In that context, ϕij is typically contoured and presented in a hazard assessment as probabilistic zones defined by the specific contours. However, because the underlying physics of these flows is not well constrained, the parameter space must be sampled widely, resulting in large probability dispersion in some cases. In the present work we globally analyze the PHM as a type of probability distribution and generate its associated measures of central tendency which form curves in 2-D space. To analyze the PHM, we must first note several of its features and state some assumptions critical to the analysis. For a PHM generated from a finite, simply connected parameter space and physically realistic governing equations,
- i.
ϕ(x) has compact support in a region Ω0⊂ℝ2, with ϕ=0 on ∂Ω0;
- ii.
; and
- iii.
there exists a (possibly unconnected) set Ω1⊂Ω0 in which ϕ(x)=1.
We will further assume that ϕ(x) is continuous and at least twice differentiable for , that is, in the regions away from the ϕ=0 and ϕ=1 contours. We focus the analysis to follow in regions away from local maxima with ϕ<1. This restriction can be mitigated by segmentation of the spatial domain as detailed below.
Formally, ϕ(x) is a cumulative distribution function (CDF) for the location of the edge of the simulated flow. This is represented schematically in Fig. 1. To see this, consider parametric curves along level set unit normals of ϕ:
parameterized by arc length s with , where and and L is the finite total Euclidean path length of xn. Note that is only calculable where . To ameliorate this, we define piecewise as
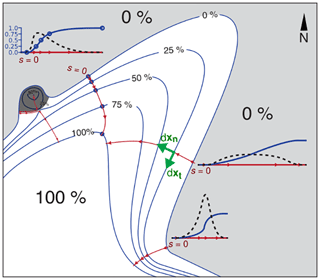
Figure 1Schematic representation of a hypothetical probabilistic hazard map (PHM) where contours (blue) are the percent of deterministic models inundating a given point in space. Steepest ascent integral curves on the PHM (xn(s)) are shown in red. Profiles for the cumulative distribution ϕ(xn(s)) (blue) and the probability density dϕ(xn(s))∕ds (black dashes) are represented schematically. The dark grey transparent region is the region of influence for the local maximum (ℛm) in which all integral curves terminate at the local maximum. Two integral curves (one inside of ℛm, one outside of ℛm) show the typical behavior of xn(s) near ∂ℛm. The set is the entire white region, Ω0 is the region bounded by the zero level set (the white region plus the dark grey region), and Ω1 is the subset of that region which is marked with 100 %.
Along each integral curve, profiles of the PHM are denoted as
where ℙ(sF≤s) is the cumulative probability that position xn(s) is farther from xn(0) than the true inundation front xn(sF) is from xn(0) as measured along the integral curve. For example, where ϕ(s)=1, the inundation front is almost surely found somewhere further back on the curve towards xn(0). Similarly, where , there is a 50 % chance of finding the true inundation front between that point (xn(s)) and either of the two endpoints of the integral curve (xn(0) and xn(L)). Because the integral curves follow the gradient, ϕ(s) is nondecreasing and along with satisfies the description of a CDF.
If local maxima less than unity are present, then the integral curves that ascend these maxima will not be valid CDFs (ϕ(s)) because they never reach the value ϕ=1. Despite this, as long as the PHM contains a finite number of local maxima less than unity (ϕ(xm)<1 where the index “m” runs over the M local maxima), then for each local maximum we may define a region ℛm which surrounds xm and is bounded by two integral curves as well as a segment of ∂Ω0 and ∂Ω1. Because local maxima are sinks for gradient-ascending integral curves, all of the integral curves that begin on will terminate at xm by definition. The two bounding integral curves are therefore defined extrinsically as those integral curves producing valid CDFs originating closest to the segment of ∂Ω0 that originates the integral curves terminating at xm. Although these regions are only defined in a weak sense, these regions are definable for practical purposes (Appendix B). If there is a saddle point between a local maximum and ∂Ω1, then the two integral curves will meet at the saddle point and no part of ∂Ω1 will make up the boundary of ℛm. In a sense, ℛm can be thought of as the shadow of trajectories that are influenced most by the local maximum ϕ(xm) (Fig. 1). We remove these regions by constructing a new set on which the remainder of the analysis is valid:
2.2 Probabilistic hazard density map
To find the PDF dϕ∕ds associated with this distribution, consider that by the chain rule
and consequently
Although this description satisfies the requirements of a PDF along each individual integral curve, it cannot be applied directly to measure the probability density in two dimensions. To measure this probability density, we generate a normalized PDF over 2-D space which we refer to as the probabilistic hazard density map (PHDM):
where
which is finite and positive in the sense of distributions. With this normalization, the integral over is unity, giving ψ(x) the properties of a PDF for the inundation front location. Consequently, the value ψ(x)dA represents the probability of finding the inundation edge in an increment of area dA. As noted, this distribution is only valid in : the region of space where local maxima in the PHM do not influence the integral curves. A proof which extends Eq. (10) to this normalization of the PHDM is given in Appendix A.
In the notional example given above for a PHM generated by a parameter space Dirac delta, given a PHM that is identically the indicator function, the PHDM is defined only in the sense of distributions because of the apparently infinite gradient at ∂dΩ(β0). However, because derivatives can be defined in the sense of distributions, the PHDM corresponding to certain input parameters is , where form the locus of points representing the certain boundary location. In this case, Ω0=Ω(β0). This scenario corresponds to the propagation of complete certainty in parameter space to complete certainty of the flow boundary location in Euclidean space.
2.3 Measures of central tendency and variance
Using these definitions, three measures of central tendency (mode, mean, median) can be generated for each integral curve, generating a locus of points (curve) for each measure parameterized by a new parameter (l) which increases along the PHM contours according to
where is a rotation matrix and xt(l) are integral curves everywhere tangent to the PHM contours (schematized in Fig. 1).
By defining a density function for the inundation edge probability distribution as in Eq. (11), a notional modal set can be constructed by connecting the maximal value of ψ on each integral curve xn. The modal set (parameterized by l) is
For the inundation hazard map, the curve xℳ(l) represents the maximum likelihood curve along which to find the inundation front. Although each distribution may not be unimodal and individual distributions may have unimodal and multimodal regions owing to the complexity of the underlying physics of the problem, this estimate gives a starting point for understanding the central tendency of the distribution.
Furthermore, we may find the mean location of the inundation by considering the first moment of each univariate PDF . For each integral curve xn(s;l) connecting a point on ∂Ω0 to a point on ∂Ω1, the first moment (mean) of dϕ∕ds may be written as
We compute this integral by parts but make a critical substitution before doing so. Note that for a new function 1−ϕ, differentiating yields dd(1−ϕ). We may substitute this into Eq. (15) and then integrate by parts:
Because ϕ(L)=1, the endpoint-evaluated terms in the limit will vanish. This allows for a simpler representation for the first moment:
This formula gives the expected value of the arc length parameter, which can be substituted to give an expected boundary location. Once μ(l) is calculated for every integral curve xn(s;l), we may connect these points to form a curve defined by
Finally, we may define a curve representing the median value of the probability distribution for inundation front location. This is simply the 50 % probability contour:
which is a level set of the hazard map. The three curves xℳ, xμ, and xmed represent different measures of the central tendency of the hazard map probability distribution.
Additionally, a measure of the variance may also be constructed for each PDF , although this requires integration of the density function over s:
The standard deviation (σ) defines a region around the mean value in that for each integral curve, the points map to points in space along the curves xμ±σ(l), forming a region about xμ(l) between xμ+σ(l) and xμ−σ(l). Higher moments of the distribution may be calculated similarly along each curve and subsequently connected.
To highlight the features of the new theory, we present three examples of its application in order of increasing complexity and realism.
3.1 Example 1: analytic model of time-dependent solidification of a viscous gravity current
A simple application of this theory is to a flow which can be calculated analytically. Here, we show the application of the above theory to the problem of time-dependent solidification of a viscous gravity current. This model used by Quick et al. (2017) is a modification of the famous model due to Huppert (1982) of the axisymmetric (radial) spread of viscous gravity currents, allowing for time-dependent viscosity where the height of the current is governed by
where g is gravitational acceleration. This model incorporates a simple model of time-dependent kinematic viscosity increase representing the solidification of the current,
where ν0 is the kinematic viscosity (ν) at time t=0 and Γ is the time it takes for the viscosity to increase by a factor of e. The solution for the release of a constant volume V0 with initial radius r0 may be stated as
where
and
Notably, Θ→Γ as t→∞, implying that eventually the current will solidify and grow to a maximum size. Consequently, when the flow dynamics have ceased, the radius of the edge of the current (rN), where the current thickness vanishes, will have reached a maximum at
To use this simple model to illustrate the probability distribution properties above, consider the case where all parameters are known precisely except for the viscosity freezing time coefficient Γ which can be constrained within a range . Because Eqs. (23) and (26) could be nondimensionalized so as to be rewritten in terms of one fundamental parameter , which is proportional to Γ, this single random parameter choice captures the underlying uncertainty in this example. Under the assumption of no prior knowledge of the likelihood of any particular value of Γ, a uniform distribution may be used to construct an inundation indicator function for this model:
To generate a PHM from this indicator function as above, the indicator function must be integrated through the parameter space. The only nonconstant segment of this integral is on the interval where
with and . This results in the PHM (Fig. 2a and c):
From the PHM, the PHDM (Fig. 2b and c) can be calculated as
and the integral curves can be calculated as
with and .
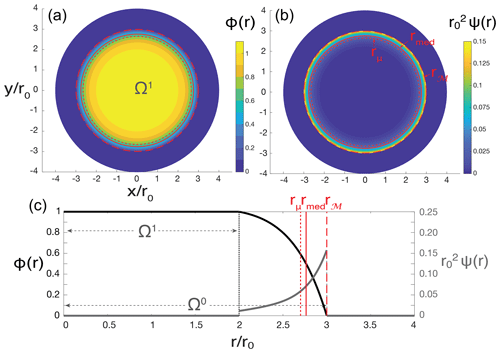
Figure 2(a) PHM and (b) PHDM examples for the freezing viscous gravity current model under a uniform sampling of the freezing rate parameter Γ. (c) One-dimensional profile of the PHM and PHDM with the distribution centers indicated. This example was calculated with and or and .
These relationships lead naturally to the estimates of the center of the distribution (Fig. 2) as defined above,
and the standard deviation,
where
where Eq. () was substituted into Eq. (), and Eqs. (15) and (20) were used to calculate Eq. (34). Higher moments of the distribution are theoretically calculable by repeated integration by parts, from which additional facts may be learned about the distribution.
These calculations can be made analytically because of the ability to write the equation of the boundary and because that equation is invertible for the unknown parameter; that is, it can be written as rN(Γ) (a boundary in Euclidean space) and as Γ(rN) (a boundary in parameter space). This example also serves to highlight the asymmetry of the PHM despite the underlying uniform distribution of physical parameters. This asymmetry is highlighted by the significant spread in the mean, median, and modal boundaries (Fig. 2).
This example was greatly simplified by the assumption of radial symmetry, allowing the distribution to be cast onto one random variable, the radius of the flow boundary, giving integral curves of constant azimuthal angle which are linear in map view. However, in most realistic cases, this is a very poor assumption and the distribution will vary between integral curves.
3.2 Example 2: Mohr–Coulomb flow on an inclined plane
To see the full realization of these concepts, a true two-dimensional problem is required. A simple example flow which had been well-studied is a lab-scale granular flow of sand down an inclined plane with a Mohr–Coulomb (MC) friction relation analogous to a natural-scale debris avalanche or landslide (Patra et al., 2005, 2018a, b; Dalbey et al., 2008; Yu et al., 2009; Webb and Bursik, 2016; Aghakhani et al., 2016). In the simulated version, a MC rheology variant of the Saint-Venant shallow water equations is solved numerically with the purpose-built solver TITAN2D (available from https://vhub.org/, Version 4.0.0, VHUB, 2016). In this setup (Fig. 3a), a 5 cm radius, 5 cm high cylindrical pile is placed 0.7 m up a 1 m long, 38.5∘ inclined plane and is allowed to flow out onto a flat runout 0.5 m long by 0.7 m wide. In accordance with MC theory, the flows were stopped locally when the sum of the drag due to internal and bed friction exceeded the gravitational forces, and the simulations were stopped globally after 1.5 s, when the flow dynamics had typically ceased (Patra et al., 2018b). In this case, the solution variable of interest h is the maximum flow height over time, that is, the maximum flow height that each point experiences through the course of the flow.
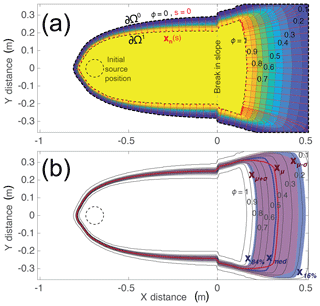
Figure 3(a) PHM contours for a Mohr–Coulomb (MC) flow on an inclined plane with integral curves xn(s) (red) connecting points on ∂Ω0 to points on ∂Ω1 as defined in the text. (b) Mean (xμ, red curve) and median (xmed, blue curve) flow boundary sets as well as regions within 1 standard deviation from the mean (red) and containing 68 % of the possible flow boundaries around the median (blue).
The uncertain parameters in the problem for a given granular medium are the internal and basal friction angles of the medium, φint and φbed respectively. To construct the PHM for this flow, 512 TITAN2D simulations were performed over a Latin-hypercube-sampled input parameter space of
To construct the indicator functions for this experiment, a thickness threshold of h0=1.0 mm was adopted. The PHM was then computed by averaging the indicator functions: a discrete analogy to Eq. (4). Owing to the discrete nature of the data, all continuous operations on the PHM were done by numerical finite differences and quadrature.
The PHM for this problem has many important characteristics, notably that the greatest dispersion in the probability contours occurs in the runout zone, owing principally to the uncertainty in φbed. Additionally, the spreading angle of the flow as a whole experiences a significant increase as the flow passes the break in slope (Fig. 3a). In order to calculate the mean flow boundary set and higher moments of this distribution, the gradient ascent curves of Eq. (5) were integrated numerically from a finite set of closely spaced points around an approximation of ∂Ω0 defined as
where J=2049 is the number of such points generated by numerical contouring. Equation (5) was integrated by Euler's method with a 1 mm step forward in s (Δsk=1 mm), thus fixing mm. This yielded discrete integral curves of varying lengths around the perimeter of the PHM (Fig. 3a). With each calculated, ϕ(sk;lj) was constructed and the parameter μj calculated on each curve, yielding an estimate of xμ(l) by interpolation of the discrete points (Fig. 3b). The standard deviations σj and the standard deviation space curves xμ±σ(l) were calculated by similar means (Fig. 3b). An important result of these calculations is that for almost every part of the runout zone, the mean flow boundary set xμ is dislocated from the median flow boundary set xmed (), indicating qualitatively the general asymmetry of this distribution. Additionally the region bounded by the curves xμ±σ is remarkably different from the region which bounds the central 68 % of the data – the percent bounded by ±σ in the normal distribution (Fig. 3). All of this indicates that for PHMs of even simple realistic flows, the underlying statistics are not only nonnormal and nonsymmetric, they are variable along the boundary of the hazard.
3.3 Example 3: PHM and PHDM construction from simulations of the 1955 debris flow in Atenquique, Mexico
Following from the previous application of the PHM statistics to a simple flow, here we present a more advanced application: construction and analysis of a PHM for a more complex flow over natural topography. This example consists of numerical modeling detailed in Bevilacqua et al. (2019) of the 1955 volcaniclastic debris flow which destroyed the village of Atenquique at the base of Nevado de Colima, Mexico. On 16 October 1955, at 10:45 LT, residents of Atenquique experienced the arrival of an 8–9 m high debris flow wave front that subsequently destroyed much of the town's buildings and infrastructure and caused more than 23 deaths (Ponce Segura, 1983; Saucedo et al., 2008). The debris flow was initiated by landsliding in the upper reaches of the Atenquique, Arroyo Seco, Los Plátanos, and Tamazula fault ravines, with a minimum initial volume of 3.2×106 m3 (Rupp, 2004; Saucedo et al., 2008). In the simulation of this flow, this volume was increased by 10 %–50 % to give volumes of m3 (Bevilacqua et al., 2019).
We analyze an ensemble of TITAN2D simulations of this flow that were generated by Bevilacqua et al. (2019) using a physically realistic rheology for a debris flow, the Voellmy–Salm (VS) rheology. This rheology is parameterized by a bed friction coefficient μVS and a velocity-dependent friction parameter ξ which approximates turbulence-induced dissipation and is uncertain over several orders of magnitude. Consequently, ξ is sampled logarithmically (Patra et al., 2018a, b). The flow was initiated from five source paraboloidal piles of material with unitary aspect ratios and volumes represented as constant fractions of the total flow volume which were proportional to the drainage size (Fig. 4a). The input parameter space ℬ for this simulation was taken as a convex subset of {(arctan (μVS), log 10(ξ), V)} with the bounds 1∘ ≤ arctan (μVS)≤ 3∘, , and . This set was determined using information about the known flow runout, flow arrival time in the town, and exclusion of ravine overflow in conjunction with a round of preliminary simulations according to a new procedure of probabilistic modeling setup (Bevilacqua et al., 2019).
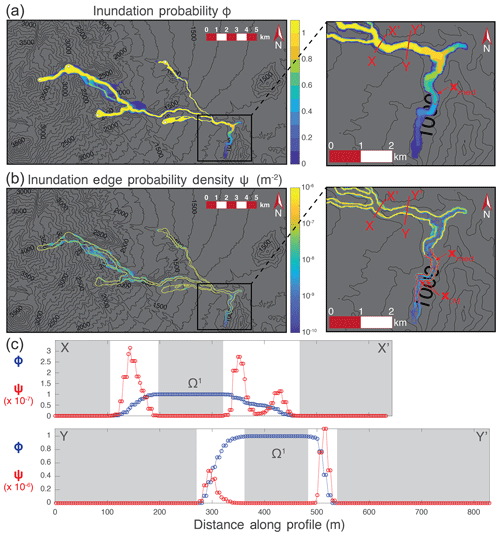
Figure 4(a) PHM and (b) PHDM for a lahar inundating Atenquique, Mexico, using the numerical model TITAN2D incorporating the parameter space described in the text. (c) Profiles of the PHM and PHDM across sections X–X′ and Y–Y′ highlighting the fact that each side of the PHM profile acts as a CDF for the location of the inundation edge with the corresponding scaled PDF given by the same profile along the PHDM. Grey background (c) indicates regions where ϕ=0 or ϕ=1 (ψ=0).
As in the previous example, the solution variable of interest is the maximum flow height over time; however, here the height threshold h0=5.0 cm is used. The 350 VS simulation indicator functions were averaged as in the previous example to obtain the PHM for this flow (Fig. 4a). For such a complex flow margin, the gradient-ascending integral curves could not be computed reliably at the resolution of the model; however, the PHDM was calculated using a discrete gradient operation, giving a sense of the maximum likelihood for the inundation boundary (Fig. 4b). Owing to the complexity of this flow and its underlying topography, profiles of the PHM and PHDM across the flow indicate that each margin of the flow is distributed nonsymmetrically, although the sense of asymmetry does not appear to be systematic (Fig. 4c). In numerous locations, the flow boundary distributions (profiles of the PHDM) are multimodal, which are interpreted to be controlled primarily by complexities in the underlying topography, relating to partial spillover of the steep bounding ravines. Of particular interest is the behavior of the PHM and PHDM at the distal margin of the flow in the town of Atenquique and as it leaves town downriver to the south and upriver to the north. To the south (downriver) the PHM decays over a very long distance (>5 km) down a constrained channel, giving small values for the PHDM along the direction of flow (Fig. 4b). Consequently in this region, the flow boundary distributions are multimodal with weaker modes more distally and only the lateral boundaries being well-defined. This portion of the flow highlights some important problems with PHMs in general; they may include regions where the distribution spans a wide range of distances and will therefore have a large standard deviation, yielding high uncertainty in the flow boundary location. The accuracy of the PDFs over the integral curves in this region is most sensitive to the number of samples affecting this region. In a finite sampling of the parameter space, these PDFs may contain spurious peaks in regions where very few models reach. For example if only a small number of models reach a region where the PHM decays over many grid cells, unless some smoothing or interpolation is applied before gradient calculation, the PHM will decay stepwise with many grid spaces between steps. When the numerical gradient is calculated over a set cell size, these steps will become peaks in the PDFs and PHDM. This problem is generally absent where the PHM step size is more comparable to the scale of the grid spacing used by the gradient operator.
This complex example highlights the need for consideration of additional probability measures than simply the probability contours. Where the flow is not narrowly confined or where spillover has occurred, the shape of the distribution becomes relevant and may yield significantly different results than estimating the likely flow boundary as one of the probability contours.
As shown by the above three examples, our theory can be applied to give consistent results between continuous, analytic models and discrete, numerical models of flows. The following discussion highlights several consequences of the theory as applied to analytic models in research and more complex numerical models in hazard assessments.
4.1 Analytic models
Although an analytic model (Quick et al., 2017) was invoked in the first example to make an exact calculation of the mean, median, mode, and standard deviation of the flow boundary, the real value of these models is that they are generally invertible and can be used to extract information about the input parameters from the properties of a given flow. Specifically, the PDF measuring the space of input parameters f can be inverted from data collected from the natural phenomena that the analytic model represents. Using the example of the freezing viscous gravity current highlighted above (Quick et al., 2017), we show that an ensemble of natural examples of such flows can be used to invert the PDF of input parameters directly from the definition of the PHM. Suppose that remote sensing or geological field work yields data on the maximum radii (rN) for an ensemble of these natural freezing gravity currents and that a natural PHM model is constructed called , which represents the discrete CDF of radii that were measured. As before, we consider a simplified case wherein the most uncertain parameter from among the collection of natural flows is the freezing rate parameter Γ. If the researcher were sufficiently confident that these assumptions and the governing equation (Eq. 21) accurately describe these flows, then the only differences between and Eq. () would arise as a consequence of the PDF f(Γ) of the natural input space being nonuniform. Consequently, because the formula for the flow boundary () is known and is invertible, the formula for the PHM can also be inverted directly in this simple case as follows:
Applying the fundamental theorem of calculus and the chain rule yields
In practice, the collected data would be in the form of a normalized histogram for the maximum flow radii. As a discrete approximation, is the associated complementary CDF for . Consequently, the PDF over parameter space could be written approximately as
where Γi are sample points at which the calculation is performed. This illustrates the general fact that the distribution of flow boundaries observed reflects the underlying parameter space PDF weighted by the Jacobian (univariate derivative in this case) of the analytic mapping from parameter space to the flow boundary location in Euclidean space. Generally, unless the analytic model predicts that the boundary of a flow (Ω(β)) is proportional to a given parameter, the input space distribution f(β) undergoes a nonlinear transformation in the construction of a PHM and PHDM. More precisely, we remark that the calculated distribution is the conditional probability density f(Γ|βk), where βk represents all of the other parameters that were assumed to be known precisely. Inverting the PHM for the joint parameter space PDF is beyond the scope of this work.
4.2 Numerical models and probabilistic hazard assessment
If the parameter space of a given inundation hazard scenario and a realistic physical model of the process are known, a simple numerical experiment can be run using classical Monte Carlo methods or other Monte Carlo variants as was done for the granular flow on an inclined plane (Patra et al., 2018b) or the 1955 Atenquique lahar (Bevilacqua et al., 2019), as well as even more sophisticated sampling methods (e.g., Bursik et al., 2012, Bayarri et al., 2015). As in the examples in this study, the hazard map and hazard density map and the associated statistics may be generated from such experiments. This may then be used to give additional information to a probabilistic assessment of the hazard rather than merely the inundation probability contours. In this context, the method outlined here is capable of generating the typical measures that would appear in routine statistical analyses of distributions. The most obvious among these is the mean flow boundary and standard deviation region. These are fundamentally newly calculable measures for PHMs and should be included in probabilistic hazard assessments.
As illustrated in the examples, the mean boundary may differ significantly from the median boundary owing to the asymmetric statistics that are inherent to typical nonlinear flows. Furthermore, this asymmetry suggests that the modal or maximum likelihood boundary may be of interest to users of these assessments as well. For the scientific component of probabilistic hazard assessments to have maximum impact and accuracy, these analyses should incorporate the full statistics of the PHM.
With new tools to calculate the moments of any given hazard edge distribution from a PHM, hazard map makers and analysts become able to estimate the likely location of the hazard edge and the uncertainty in that estimate. As numerical modeling capabilities continue to grow, the increased ease and speed of this type of analysis will allow the scientific community to quickly construct the PHM, PHDM, the mean hazard boundary curve, standard deviation region, and higher moments of the hazard boundary distribution, giving improved estimates of the true hazard zone. Although this theory is useful for many applications where probabilities are given spatially, further work is needed to constrain which types of hazard assessments and models are most suitable for this analysis and how best to blend this scientific information within existing hazard-map-making procedures. Similarly, additional work is required to study the probabilistic inverse problem further than the simple example given and to evaluate the use of this theory in a time-dependent context. Overall, the analysis put forth here significantly enhances the study of spatial probabilistic hazards, yielding new estimates of the likely hazard boundary and the uncertainty in those estimates.
Data are available in the references, specifically in Patra et al. (2018a, b) (https://doi.org/10.1007/978-3-319-93701-4_57 and https://arxiv.org/abs/1805.12104) and the Supplement of Bevilacqua et al. (2019) (https://doi.org/10.5194/nhess-19-791-2019). The fourth release of TITAN2D is available from https://vhub.org (VHUB, 2016).
Using the definition of the integral curves in the text as steepest ascent integral curves xn(s) such that
with where and , we prove the following lemma.
Lemma: PHDM normalization. Consider a probabilistic hazard map (PHM) ϕ(x) with the following properties (as given in the text):
- i.
ϕ(x) has compact support in a region Ω0⊂ℝ2, with ϕ=0 on ∂Ω0.
- ii.
.
- iii.
There exists a (possibly unconnected) set Ω1⊂Ω0 in which ϕ(x)=1.
- iv.
.
- v.
If ϕ has local maxima ϕ(xm)<1 with m∈1 … M, then each xm can be surrounded by a region of influence ℛm bounded by integral curves as defined in the text.
Define
Then
Proof. Consider the level sets of ϕ(x) as integral curves everywhere tangent to the level sets, given by
where is a rotation matrix. The curves xt(l) are the level sets of ϕ. By invoking the tangent curves and parameterizing each normal curve xn(s;l), each PDF may be extended away from a single integral curve:
Integration through l yields an integral of the gradient magnitude over with the area element parameterized in local orthonormal curvilinear coordinates by (s, l) which are derived from the PHM instead of ordinary space. Since both sets of integral curves (xn, xt) are parameterized by arc length, then dA(x)=dA(s, l). Because of these facts, the value of the integration will depend on the ϕ particular to the problem under consideration. Note that, in the coordinates (s, l), each of the domains of influence related to local maxima less than unity (ℛm) is a rectilinear patch of (s, l) space (segment of l∈[0, ∞)) which is removed, leaving the integration domain of l which contains gaps:
The right hand side of Eq. (A3) can then be evaluated by invoking a special case of the divergence theorem. Introducing an outward unit normal ν on and noting that
the divergence theorem gives
From this result, integration of Eq. () will yield
which is finite and positive due to the smoothness assumed in defining the hazard map ϕ(x) and the fact that is everywhere nonnegative. In cases where the gradient of the PHM tends to infinity, the smoothness of the PHM must be modified in the sense of distributions, allowing derivatives and integrals on the PHM in the sense of distributions. This defines the PHDM normalization Q and proves the lemma.
The following procedure is designed to simplify and condense the many steps involved in the above analysis. This recipe has been written as a blueprint for carrying out the analysis using a numerical model of the process in question. This procedure assumes that a numerical model of the process has already been selected.
-
Identify the collection of uncertain input parameters (β) that are to be varied for the experiment as well as their ranges, correlation structure, and joint distribution. This may be done by the methods of Bevilacqua et al. (2019) or other methods chosen for the particular application. This process generates the joint PDF f(β) measuring the input space.
-
Generate random sample input vectors β distributed according to f and run the numerical model on these inputs. For example, Latin hypercube sampling is a well-established procedure for defining pseudorandom designs of samples in ℝn for multivariate uniform probability distributions (McKay et al., 1979; Stein, 1987; Owen, 1992). If all of the parameters are uncorrelated but nonuniform, then each random variable may be sampled independently according to its marginal distribution alone. If f measures a correlated set of input random variables, then a sampling scheme must be used which respects the correlation structure and marginal distributions of the random variables. This sampling is very straightforward for the multivariate normal distribution which has implementations in most scientific computing languages; however, other distributions require different techniques such as the NORTA (NORmal To Anything) process (Cairo and Nelson, 1997). The number of samples generated is directly related to the smoothness of the output PHM to be created.
-
Identify the threshold of interest for a given model observable and generate the indicator function for each model run according to the threshold. In practice, this can be realized as a sequence of grids, each of which is an element-wise indicator. In a MATLAB environment, this could be accomplished for each grid with the following syntax in which the indicator and the variable of interest are arrays of double-precision floating-point:
INDICATOR=double(VARIABLE>THRESHOLD_VALUE). -
The PHM ϕ is obtained by performing an element-wise average of all of these indicator grids. The random sampling according to f(β) ensures that the element-wise average represents the underlying distribution. Some smoothing of ϕ may be required for further processing to reduce the effects of finite input sampling.
-
Generate the level set unit normal vector field for ϕ using a numerical gradient operation g≈∇ϕ which can be implemented in most scientific computing language. Each component of g is a grid of the same size as ϕ. Calculate the unit normal vector field as
or in a MATLAB script:
[g_x,g_y] =gradient(PHI,dx,dy)g_mag= (g_x.^2+g_y.^2).^0.5n_x=g_x./g_magn_y=g_y./g_magn_x(isnan(n_x))=0n_y(isnan(n_y))=0. -
Generate the gradient-ascending integral curves xn. This is done numerically by any gradient ascent algorithm for solving
may be computed for each step by interpolating the vector field at the point xn(sk). The initial position for each curve is given by the set of points output by a numerical contouring algorithm to find points very close to the ϕ=0 level set. A large number output points should be specified in the contouring. In practice, a very small level set value is chosen for this contouring ( in our example 2). In general, small values of Δsk give smoother curves. Iteration follows for each curve until g(xn(sk))→0 with either (a) ϕ(xn(sk))=1 or (b) ϕ(xn(sk))<1. These two conditions ensure that either the integral curve ends on ∂Ω1 (condition a) or a local maximum ϕ(xm) (condition b).
-
Generate the valid regions of the PHM by eliminating all regions in which integral curves terminate at local maxima. In practice, this could be accomplished by generating an indicator grid in which all array elements within a certain neighborhood of these curves are set to zero and all other elements are set to 1.
-
Generate the PHDM using the gradient magnitude that was already calculated. For the normalizing constant Q, choose a numerical integration scheme (trapezoidal rule, Simpson's rule, Monte Carlo, or others) and compute the integral over the entire grid of the gradient magnitude filtered by the valid region indicator created in the last step. The PHDM is then given as . Any integration of ψ must be computed with the same method.
-
To compute the mean on each curve, treat the sequence ϕk=ϕ(xn(sk)) as samples of a CDF over the sequence sk, numerically approximate the formula
with a suitable technique (trapezoidal rule, Simpson's rule, or others), and calculate the mean position on each curve as xμ=xn(μ) by interpolation. The variance on each curve can be found similarly by numerical approximation of
Higher moments can be calculated by similar formulas involving the term 1−ϕ(s) which comes from integration by parts of the classical probability distribution moment formulas. The median position xmed on each curve is the point at which and the mode or maximum likelihood position xℳ is at the maximum of ψ(xn(s)), which can be found by interpolation of the PHDM along the computed curves. Each xμ, xmed, and xℳ is then connected for all of the integral curves, making a set of curves for each of the mean, median, and mode, and a region bounded by two curves for the standard deviation.
DMH and MIB conceived of the main concepts. DMH developed the mathematical results and wrote the manuscript. AB implemented and performed the numerical simulations and contributed to the mathematics. All authors interpreted and discussed the results, provided comments and feedback for the manuscript, and approved the publication.
The authors declare that they have no conflict of interest.
We acknowledge the support of NASA grant NNX12AQ10G; the JPSS PGRR program under NOAA–University of Wisconsin CIMSS Cooperative Agreement number NA15NES4320001; NSF awards 1339765, 1521855, and 1621853; and private donations to the University at Buffalo Foundation. Additionally, we thank the University at Buffalo Center for Computational Research as well as the helpful comments of two anonymous reviewers.
This research has been supported by the National Aeronautics and Space Administration (grant no. NNX12AQ10G), the University at Buffalo Foundation, the National Science Foundation (grant nos. 1339765, 1521855, and 1621853), and the National Oceanic and Atmospheric Administration (grant no. NA15NES4320001).
This paper was edited by Giovanni Macedonio and reviewed by two anonymous referees.
Aghakhani, H., Dalbey K., Salac, D., and Patra, A. K.: Heuristic and Eulerian interface capturing approaches for shallow water type flow and application to granular flows, Comput. Meth. Appl. Mech. Eng., 304, 243–264, https://doi.org/10.1016/j.cma.2016.02.021, 2016. a
Bayarri, M. J., Berger, J. O., Calder, E. S., Patra, A. K., Pitman, E. B., Spiller, E. T., and Wolpert, R. L.: Probabilistic Quantification of Hazards: A Methodology Using Small Ensembles of Physics-based Simulations and Statistical Surrogates, Int. J. Uncertain. Quant., 5, 297–325, https://doi.org/10.1615/Int.J.UncertaintyQuantification.2015011451, 2015. a, b
Bevilacqua, A.: Doubly stochastic models for volcanic hazard assessment at Campi Flegrei caldera, Thesis, 21, Edizioni della Normale, Birkhäuser/Springer, Pisa, 2016. a
Bevilacqua, A., Neri, A., Bisson, M., Esposti Ongaro, T., Flandoli, F., Isaia, R., Rosi, M., and Vitale, S.: The Effects of Vent Location, Event Scale, and Time Forecasts on Pyroclastic Density Current Hazard Maps at Campi Flegrei Caldera (Italy), Front. Earth. Sci., 5, 1-16, https://doi.org/10.3389/feart.2017.00072, 2017. a, b
Bevilacqua, A., Patra, A. K., Bursik, M. I., Pitman, E. B., Macías, J. L., Saucedo, R., and Hyman, D.: Probabilistic forecasting of plausible debris flows from Nevado de Colima (México) using data from the Atenquique debris flow, 1955, Nat. Hazards Earth Syst. Sci., 19, 791–820, https://doi.org/10.5194/nhess-19-791-2019, 2019. a, b, c, d, e, f, g
Biass, S., Falcone, J., Bonadonna, C., Di Traglia, F., Pistolesi, M., Rosi, M., and Lestuzzi, P: Great balls of fire: A probabilistic approach to quantify the hazard related to ballistics – A case study at La Fossa Volcano, Vulcano Island, Italy, J. Volcanol. Geotherm. Res., 325, 1–14 https://doi.org/10.1016/j.jvolgeores.2016.06.006, 2016. a, b
Bursik, M., Jones, M., Carn, S., Dean, K., Patra, A., Pavolonis, M., Pitman, E. B., Singh, T., Singla, P., Webley, P., Bjornsson, H., and Ripepe, M.: Estimation and propagation of volcanic source parameter uncertainty in an ash transport and dispersal model: Application to the Eyjafjallajokull plume of 14–-16 april 2010, Bull. Volcanol., 74, 2321–2338, https://doi.org/10.1007/s00445-012-0665-2, 2012. a, b, c, d
Cairo, M. C. and Nelson, B. L.: Modeling and generating random vectors with arbitrary marginal distributions and correlation matrix, Technique Report, Department of Industrial Engineering and Management Science, Northwestern University, Evanston, IL, 1997 a
Calder, E., Wagner, K., and Ogburn, S.: Volcanic hazard maps, in: Global Volcanic Hazards and Risk, edited by: Loughlin, S., Sparks, S. , Brown, S., Jenkins, S., and Vye-Brown, C., Cambridge University Press, Cambridge, 335–342, 2015. a, b
Connor, C., Bebbington, M., and Marzocchi, W.: Ch 51 – Probabilistic volcanic hazard assessment, in: Encyclopedia of Volcanoes, 2nd Edn., edited by: Sigurdsson, H., Academic Press, Amsterdam, 897–910, https://doi.org/10.1016/B978-0-12-385938-9.00051-1, 2015. a
Dalbey, K., Patra, A. K., Pitman, E. B., Bursik, M. I., and Sheridan, M. F.: Input uncertainty propagation methods and hazard mapping of geophysical mass flows, J. Geophys. Res.-Solid, 113, 1–16, https://doi.org/10.1029/2006JB004471, 2008. a
DeGroot, M. H. and Schervish, M. J.: Probability and Statistics, 4th Edn., Pearson Education Limited, Boston, 2012. a
Gallant, E., Richardson, J., Connor, C., Wetmore, P., and Connor, L.: A new approach to probabilistic lava flow hazard assessments, applied to the Idaho National Laboratory, eastern Snake River Plain, Idaho, USA, Geology, 46, 895, https://doi.org/10.1130/G45123.1, 2018. a, b
Geist, E. L., and Parsons, T.: Probabilistic analysis of tsunami hazards, Nat. Hazards, 37, 277–314, https://doi.org/10.1007/s11069-005-4646-z, 2006. a
Grezio, A., Babeyko, A., Baptista, M. A., Behrens, J., Costa, A., Davies, G., Geist, E., Glimsdal, S., González, F. I., Griffin, J., Harbitz, C. B., LeVeque, R. J., Lorito, S., Løvholt, F., Omira, R., Mueller, C., Paris, R., Parsons, T., Polet, J., Power, W., Selva, J., Sørensen, M. B., and Thio, H. K.: Probabilistic tsunami hazard analysis: Multiple sources and global applications, Rev. Geophys., 55, 1158–1198, https://doi.org/10.1002/2017RG000579, 2017. a
Huppert, H. E.: The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface, J. Fluid Mech., 121, 43–58, https://doi.org/10.1017/S0022112082001797, 1982. a
Kvaerna, T. and Ringdal, F.: Seismic threshold monitoring for continuous assessment of global detection capability, Bull. Seismol. Soc. Am., 89, 946 946–959, 1999. a
Madankan, R., Singla, P., Patra, A., Bursik, M., Dehn J., Jones, M., Pavolonis, M., Pitman, E. B., Singh, T., and Webley, P.: Polynomial Chaos Quadrature-based Minimum Variance Approach for Source Parameters Estimation, Proc. Comput. Sci., 9, 1129–1138, https://doi.org/10.1016/j.procs.2012.04.122, 2012. a
McKay, M. D., Beckman, R. J., and Conover, W. J.: A comparison of three methods for selecting values of input variables in the analysis of output from a computer code, Technometrics, 21, 239–245, https://doi.org/10.2307/1268522, 1979. a
Neri, A., Bevilacqua, A., Esposti Ongaro, T., Isaia, R., Aspinall, W. P., Bisson, M., Flandoli, F., Baxter, P. J., Bertagnini, A., Iannuzzi, E., Orsucci, S., Pistolesi, M., Rosi, M., and Vitale, S.: Quantifying volcanic hazard at Campi Flegrei caldera (Italy) with uncertainty assessment: 2. Pyroclastic density current invasion maps, J. Geophys. Res.-Solid, 120, 2330–2349, https://doi.org/10.1002/2014JB011776, 2015. a
Owen, A. B.: A Central Limit Theorem for Latin Hypercube Sampling, J. Roy. Stat. Soc. B, 54, 541–551, https://doi.org/10.1111/j.2517-6161.1992.tb01895.x, 1992. a
Patra, A. K., Bauer, A. C., Nichita, C. C., Pitman, E. B., Sheridan, M. F., Bursik, M., Rupp,. B., Webber, A., Stinton, A. J., Namikawa, L. M., and Renschler, C. S.: Parallel adaptive numerical simulation of dry avalanches over natural terrain, J. Volcanol. Geotherm. Res., 139, 1–21, https://doi.org/10.1016/j.jvolgeores.2004.06.014, 2005. a
Patra, A. K., Bevilacqua, A., and Akhavan-Safaei, A.: Analyzing Complex Models using Data and Statistics, in: Computational Science – ICCS 2018, Lecture Notes in Computer Science, vol. 10861, edited by: Shi Y., Fu, H., Tian, Y., Krzhizhanovskaya, V. V., Lees, M. H., Dongarra, J., and Sloot, P. M. A., Springer, Cham, https://doi.org/10.1007/978-3-319-93701-4_57, 2018a. a, b, c
Patra, A. K., Bevilacqua, A., Akhavan-Safaei, A., Pitman, E., Bursik, M., and Hyman, D.: Comparative analysis of the structures and outcomes of geophysical flow models and modeling assumptions using uncertainty quantification, arXiv, https://arxiv.org/abs/1805.12104 (last access: 17 June 2019), 2018b. a, b, c, d, e, f, g
Ponce Segura, J. M.: Historia de Atenquique, Talleres litográficos Vera, Guadalajara, Jalisco, México, 151 pp., 1983. a
Quick, L. C., Glaze, L. S., and Baloga, S. M.: Cryovolcanic emplacement of domes on Europa, Icarus, 284, 477–488, https://doi.org/10.1016/j.icarus.2016.06.029, 2017. a, b, c
Rupp, B.: An analysis of granular flows over natural terrain, MS Thesis, University at Buffalo, Buffalo, 2004. a
Sandri, L., Costa, A., Selva, J., Tonini, R., Macedonio, G., Folch, A., and Sulpizio, R.: Beyond eruptive scenarios: Assessing tephra fallout hazard from Neapolitan volcanoes, Sci. Rep., 6, 24271, https://doi.org/10.1038/srep24271, 2016. a, b
Saucedo, R., Macías, J. L., Sarocchi, D., Bursik, M., and Rupp, B.: The rain-triggered Atenquique volcaniclastic debris flow of October 16, 1955 at Nevado de Colima volcano, Mexico, J. Volcanol. Geotherm. Res., 173, 69–83, https://doi.org/10.1016/j.jvolgeores.2007.12.045, 2008. a, b
Spiller, E. T., Bayarri, M. J., Berger, J. O., Calder, E. S., Patra, A. K., Pitman, E. B., and Wolpert, R. L.: Automating Emulator Construction for Geophysical Hazard Maps, SIAM/ASA J. Uncertain. Quant., 2, 126–152, https://doi.org/10.1137/120899285, 2014. a
Splitt, M. E., Lazarus, S. M., Collins, S., Botambekov, D. N., and Roeder, W. P.: Probability distributions and threshold selection for Monte Carlo–Type tropical cyclone wind speed forecasts, Weather Forecast., 29, 1155–1168, https://doi.org/10.1175/WAF-D-13-00100.1, 2014. a
Stefanescu, E. R., Bursik, M., Cordoba, G., Dalbey, K., Jones, M. D., Patra, A. K., Pieri, D. C., Pitman, E. B., and Sheridan, M. F.: Digital elevation model uncertainty and hazard analysis using a geophysical flow model, P. Roy. Soc. A, 468, 1543–1563, https://doi.org/10.1098/rspa.2011.0711, 2012. a, b
Stein, M.: Large Sample Properties of Simulations Using Latin Hypercube Sampling, Technometrics, 29, 143–151, https://doi.org/10.2307/1269769, 1987. a
Thompson, M. A., Lindsay, J. M., and Gaillard, J.: The influence of probabilistic volcanic hazard map properties on hazard communication, J. Appl. Volcanol., 4, 1–6, https://doi.org/10.1186/s13617-015-0023-0, 2015. a, b
Tierz, P., Sandri, L., Costa, A., Zaccarelli, L., Di Vito, M. A., Sulpizio, R., and Marzocchi, W.: Suitability of energy cone for probabilistic volcanic hazard assessment: Validation tests at Somma-Vesuvius and Campi Flegrei (Italy), Bull. Volcanol., 78, 1–15, https://doi.org/10.1007/s00445-016-1073-9, 2016. a
Tierz, P., Stefanescu, E. R., Sandri, L., Sulpizio, R., Valentine, G. A., Marzocchi, W., and Patra, A. K.: Towards quantitative volcanic risk of pyroclastic density currents: Probabilistic hazard curves and maps around Somma-Vesuvius (Italy), J. Geophys. Res.-Solid, https://doi.org/10.1029/2017JB015383, 123, 6299–6317, 2018. a
VHUB: Titan2D Mass-Flow Simulation Tool, v 4.0.0, available at: http://vhub.org/resources/titan2d, last access: 23 June 2016. a, b
Wagner, K., Ogburn, S. E., and Calder, E. S.: Volcanic Hazard Map Survey v3 (clean), available at: https://vhub.org/resources/3775 (last access: 17 June 2019), 2015. a
Webb, A. and Bursik, M.: Granular flow experiments for validation of numerical flow models, University at Buffalo, Buffalo, available at: https://vhub.org/resources/4058 (last access: 17 June 2019), 2016. a
Yu, B., Dalbey, K., Webb, A., Bursik, M., Patra, A. K., Pitman, E. B., and Nichita, C.: Numerical issues in computing inundation areas over natural terrains using Savage–Hutter theory, Nat. Hazards, 50, 249–267, https://doi.org/10.1007/s11069-008-9336-1, 2009. a





