the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Statistical analysis for satellite-index-based insurance to define damaged pasture thresholds
Juan José Martín-Sotoca
Antonio Saa-Requejo
Rubén Moratiel
Nicolas Dalezios
Ioannis Faraslis
Ana María Tarquis
Vegetation indices based on satellite images, such as the normalized difference vegetation index (NDVI), have been used in countries like the USA, Canada and Spain for damaged pasture and forage insurance over the last few years. This type of agricultural insurance is called satellite-index-based insurance (SIBI). In SIBI, the occurrence of damage is defined as normal distributions. In this work a pasture area at the north of the Community of Madrid (Spain) has been delimited by means of Moderate Resolution Imaging Spectroradiometer (MODIS) images. A statistical analysis of NDVI histograms was applied to seek for alternative distributions using the maximum likelihood method and χ2 test. The results show that the normal distribution is not the optimal representation and the generalized extreme value (GEV)
distribution presents a better fit through the year based on a quality
estimator. A comparison between normal and GEV is shown with respect to the
probability under a NDVI threshold value throughout the year. This suggests that
an a priori distribution should not be selected and a percentile methodology
should be used to define a NDVI damage threshold rather than the average and
standard deviation, typically of normal distributions.
Highlights.
-
The GEV distribution provides better fit to the NDVI historical observations than the normal one.
-
Differences between normal and GEV distributions are higher during spring and autumn, which are transition periods in the precipitation regimen.
-
NDVI damage threshold shows evident differences using normal and GEV distributions both covering the same probability (24.20 %).
-
NDVI damage threshold values based on percentile calculation are proposed as an improvement in the index-based insurance in damaged pasture.
Agricultural insurance addresses the reduction of the risk associated with crop production and animal husbandry. The concept of index-based insurance (IBI) attempts to achieve settlements based on the value taken by an objective index rather than on a case-by-case assessment of crop or livestock losses (Gommes and Kayitakire, 2013). Indeed, the goal of IBI policy remains to develop an affordable tool for all producers, including smallholders. Specifically, IBI can constitute a safety net against weather-related risks for all members of the farming community, thereby increasing food security and reducing the vulnerability of rural populations to weather extremes. Moreover, IBI can be associated with credits for insured smallholders, due to the fact that the risk of nonrepayment for lenders is reduced, which encourages the use of agricultural inputs and equipment, leading to increased and more stable crop production. Over the past decade, the importance of weather-index-based insurances (WIBIs) for agriculture has been increasing, mainly in developing countries (Gommes and Kayitakire, 2013). This interest can be explained by the potential that IBI constitutes a risk management instrument for small farmers. Indeed, it can be considered within the context of renewed attention to agricultural development as one of the milestones of poverty reduction and increased food security, as well as the accompanying efforts from various stakeholders to develop agricultural risk management instruments, including agricultural insurance products.
Farmers need to protect their land and crops specifically from drought in arid and semiarid countries, since their production may directly depend mainly on the impacts of this particular natural hazard. Insurance for drought-damaged lands and crops is currently the main instrument and tool that farmers can resort to in order to deal with agricultural production losses due to drought. Many of these insurances are using satellite vegetation indices (Rao, 2010); thus they are also called satellite-index-based insurances (SIBIs). SIBIs have some advantages over WIBIs, such as cost-effective information and acceptable spatial and temporal resolution. They do not, however, resolve the issue of basis risk, i.e., potential unfairness to insurance takers (Leblois, 2012). Moreover, the very nature of an index-based product creates the chance that an insured party may not be paid when they suffer loss. For this reason, in some countries (Spain) they have named this SIBI “damaged in pasture” to cover not only drought even though this is the main cause.
It is highly recognized that shortage of water has many implications for agriculture, society, the economy and ecosystems. Specifically, its impact on water supply, crop production and rearing of livestock is substantial in agriculture. Knowing the likelihood of drought is essential for impact prevention (Dalezios, 2013). Drought severity assessment can be approached in different ways: through conventional indices based on meteorological data, such as temperature, rainfall and moisture (Niemeyer, 2008), as well as through remote sensing indices based on images usually taken by artificial satellites (Lovejoy et al., 2008) or drones. In the second group, satellite vegetation indices (SVIs) are found, which can quantify green vegetation and soil moisture through the soil water index (Gouveia et al., 2009) combining different spectral reflectances. Thus, they are one of the main ways to quantitatively assess drought severity.
At the present time, several satellites (NOAA, TERRA, DEIMOS, etc.) can provide this spectral information with different spatial resolution. Some series with a high temporal frequency are freely available – those from NOAA satellites and Terra. The most widely known SVI is the normalized difference vegetation index (NDVI). It follows the principle that healthy vegetation mainly reflects the near-infrared frequency band. There are several other important SVIs, such as the soil adjusted vegetation index (SAVI) and enhanced vegetation index (EVI), that incorporate soil effects and atmospheric impacts, respectively. An important point of SIBI is when damage occurs. To measure this, a SVI threshold value is defined mainly based on statistics that apply to normal distributed variables: average and standard deviation. When current SVI values are below this threshold value for a period of time, insurance recognizes that damage is occurring, most of the time drought, and then it begins to pay compensation to farmers.
Important NDVI-based indices for detecting drought are the NDVI anomalies (NDVIA) and standardized vegetation index (SVI). NDVIA and SVI have been successfully used to monitor drought conditions over different regions in the world (Nanzad et al., 2019; Li et al., 2014). NDVIA is calculated as the difference between the NDVI value for a specific time period (e.g., week, month) and the long-term mean value for that period. SVI was developed by Peters et al. (2002) and obtains the probability from normal NDVI distributions over multiple years of data for a specific time period (Anyamba and Tucker, 2012; Bayarjargal et al., 2006). It is defined as
where is the long-term mean NDVI in the period i, σNDVI is the standard deviation of NDVI in the period i and NDVIi is the current NDVI value in the time period i. Using only the first and second statistical moment, the average and the square root of variance, the assumption of normality is implicit in this type of drought NDVI indicator. The normality assumption is challenged in this study.
WIBI aims to protect farmers against weather-based disasters such as droughts, frosts and floods. A WIBI policy links possible insurance payouts with the weather requirements of the crop being insured: the insurer pays an indemnity whenever the realized value of the weather index meets a specified threshold. Whereas payouts in traditional insurance programs are related to actual crop damages, a farmer insured under a WIBI contract may receive a payout. A current difficulty in the wide implementation of WIBI is the weakness of indices. Indeed, there is certainly a need for more efficient indices based on the additional experience gained from the implementation of WIBI products in the developing world. Current trends in index technology are exciting and they actuate high expectations, especially the development of yield indices and the use of remote sensing inputs. Risk protection and insurance illiteracy constitute another difficulty, which has to be addressed by training and awareness raising at all levels, from farmers to farmers' associations, microinsurance partners, and senior decision-makers in insurance, banking and politics (Bailey, 2013). It is essential that all stakeholders (especially the insured) perfectly understand the principles of IBI, as otherwise the insurer, even the whole concept of insurance, is at risk of reputation loss for years or decades.
There is currently a lack of technical capacity in the insurance sectors of most developing countries, which is a constraint to the scaling up and further development of WIBI (Gommes and Kayitakire, 2013). Specifically, although it is possible to design an index product and assist in the rollout, marketing and sales, such assistance is not possible on a wide scale, simply because there is a lack of qualified expertise. Indeed, it usually requires mathematical modeling, data manipulation and expertise in crop simulation to design an index. Nevertheless, it is possible to structure insurance with multiple indices, but this increases the complexity of the product and makes it difficult for farmers to comprehend it. Basis risk is also a particular problem for index products, which is frequently caused by the fact that measurements of a particular variable, such as rain, may differ at the insurer's measurement site and in the farmer's field. This also creates problems for insurance providers. Indeed, part of the reason the scaling up of index products has failed is that both insurers and farmers suffer from this basis risk.
Currently, to mitigate impacts of climate-related reduced productivity of French grasslands, several studies have been developed to design new insurance-scheme-based indemnity payouts to farmers on a forage production index (FPI) (Roumiguié et al., 2015, 2017). Two examples of SIBIs are presented in two different countries: the USA and Spain. In particular, in the USA there are several insurance programs for pasture, rangeland and foraging, which use various indexing systems (rainfall and vegetation indices) and are promoted by the Unites States Department of Agriculture (USDA) (Maples et al., 2016; USDA, 2018). NDVI is the index chosen in the vegetation index program, and it is obtained from the AVHRR (Advanced Very High Resolution Radiometer) sensor aboard NOAA satellites. Average, maximum and minimum NDVI values are obtained from a historical series with the aim of calculating a trigger value. The insurer decides the quantity of compensation by comparing this trigger with the current value. On the other hand, in Spain insurance for damaged pasture is available from the Spanish System of Agricultural Insurance (BOE, 2013). This insurance defines a damage event through NDVI values obtained from the MODIS sensor aboard the TERRA satellite of NASA. In this insurance, NDVI threshold values (NDVIth) are calculated by subtracting several times (k=0.7 or k=1.5) standard deviation to average within a homogeneous area:
where μ and σ are the average and standard deviation of NDVI respectively. The average and standard deviation are derived supposing normal distributions in the historical data (Goward et al., 1985; Hobbs, 1995; Fuller, 1998; Al-Bakri and Taylor, 2003; Turvey and Mclaurin, 2012; De Leeuw et al., 2014).
The aim of this paper is to find a more realistic statistical NDVI distribution without the a priori assumption that variables follow a normal distribution, typically for current SIBI methodology. In order to achieve this, the maximum likelihood method (MLM) is fitted to a historical series of NDVI values in a pasture land area in Spain (Community of Madrid). Different types of asymmetrical distributions are examined with the aim to find a better fit than normal. To eliminate some noise in the historical series, an original method is applied consisting of using the hue–saturation–lightness (HSL) color model. Finally, the Chi-square test (χ2 test) has been used to check the goodness of fit for all considered distributions.
2.1 Vegetation index
The differences of the reflectance of green vegetation in parts of the electromagnetic radiation spectrum, namely visible and near infrared, provide an innovative method for monitoring surface vegetation from space. Specifically, the spectral behavior of vegetation cover in the visible (0.4–0.7 mm) and near infrared (0.74–1.1, 1.3–2.5 mm) offers the possibility to monitor from space the changes in the different stages of cultivated and uncultivated plants taking also into account the corresponding behavior of the surrounding microenvironment (Ortega-Farias et al., 2016). Indeed, from the visible part of the electromagnetic radiation spectrum it is possible to draw conclusions about the rate photosynthesis, whereas from the near infrared inferences are extracted about the chlorophyll density and the amount of canopy in the plant mass, as well as the water content in the leaves, which is also linked directly to the rate of transpiration with impacts to physiological process of photosynthesis. Usually, data from the NOAA/AVHRR series of polar orbit meteorological satellites are used with low spatial resolution (1.1 km2) and a recurrence interval at least twice daily from the same location. Several algorithms combining channels of the red (RED), the near infrared (NIR) and green (GREEN) have been proposed, which provide indices sensitive to green vegetation.
NDVI uses two frequency bands: red band (660 nm) and near-infrared band (860 nm). Absorption of red band is related to photosynthetic activity and reflectance of near-infrared band is related to the presence of vegetation canopies (Flynn, 2006). In drought periods, NDVI values can reduce significantly; therefore many researchers have used this index to measure drought events in recent years (Dalezios et al., 2014). To calculate NDVI we will use this mathematical formula:
where IR and R are reflectance values in the near-infrared band and red band, respectively. NDVI values below zero indicate no photosynthetic activity and are characteristic of areas with large accumulation of water, such as rivers, lakes or reservoirs. The higher the NDVI value is, the greater the photosynthetic activity and vegetation canopies are.
In this paper the NDVI is used, which is a widely known index with a multitude of applications over time. The NDVI is suited for monitoring of total vegetation, since it partly compensates for the changes in light conditions, land slope and field of view (Kundu et al., 2016). In addition, clouds, water and snow show higher reflectance in the visible than in the near infrared; thus, they have negative NDVI values. Indeed, bare and rocky terrain show vegetation index values close to zero. Moreover, the NDVI constitutes a measure of the degree of absorption by chlorophyll in the red band of the electromagnetic spectrum. In summary, the NDVI is a reliable index of the chlorophyll density on the leaves, as well as the percentage of the leaf area density over land; thus, NDVI constitutes a credible measure for the assessment of dry matter (biomass) in various species' vegetation cover (Dalezios, 2013). It is clear from the above that the NDVI is an index closely related to growth and development of plants, which can effectively monitor surface vegetation from space.
The continuous increase in the NDVI value during the growing season reflects the vegetative and reproductive growth due to intense photosynthetic activity, as well as the satisfactory correlation with the final biomass production at the end of a growing period. On the other hand, the gradual decrease in the NDVI values signifies stress due to a lack of water or extremely high temperatures for the plants, leading to a reduction of the photosynthetic rate and ultimately a qualitative and quantitative degradation of plants. NDVI values above zero indicate the existence of green vegetation (chlorophyll), or bare soil (values around zero), whereas values below zero indicate the existence of water, snow, ice and clouds.
2.2 Database
The scientific research satellite Terra (EOS AM-1) has been chosen to provide necessary information to calculate NDVI in the study area. This satellite was launched into orbit by NASA on 18 December 1999. The MODIS sensor aboard this satellite collects information of different reflectance bands. MODIS information is organized by products. The product used in this study was MOD09A1 (LP DAAC, 2014). MOD09A1 incorporates seven frequency bands: band 1 (620–670 nm), band 2 (841–876 nm), band 3 (459–479 nm), band 4 (545–565 nm), band 5 (1230–1250 nm), band 6 (1628–1652 nm) and band 7 (2105–2155 nm). The bands used to calculate NDVI are band 1 for red frequency and band 2 for near-infrared frequency. MOD09A1 provides georeferenced images with a pixel resolution of 500 m × 500 m. Each MOD09A1 pixel contains the best possible L2G observation during an 8 d period as selected on the basis of high observation coverage, low view angle, the absence of clouds or cloud shadow, and aerosol loading.
The period of time selected in this study was from 2002 to 2017.
Daily data from a principal station of the meteorological network were utilized during the period studied (2002–2017). Meteorological station is located in 40∘41′46′′ N 3∘45′54′′ W (elevation 1004 m a.s.l.), less than 2 km from the study area (AEMET, 2017).
2.3 Site description
Six pixels (500 m × 500 m) are considered located in a pasture area at the north of the Community of Madrid (Spain) between the municipalities of Soto del Real and Colmenar Viejo. The study area is located between meridians 3∘45′00′′ and 3∘47′00′′ W and parallels 40∘42′00′′ and 40∘44′00′′ N approximately (see Fig. 1).
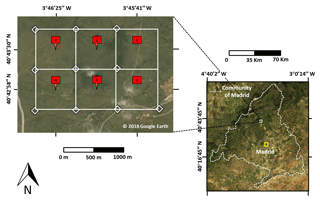
Figure 1The study area is in the center of the Iberian Peninsula (Community of Madrid). RGB image of the 6-pixel area used for the case study is shown (© Google Earth and MODIS images).
The annual mean temperature ranges during the study period from 12.7 to 13.8 ∘C, and annual mean precipitation ranges from 360 to 781 mm. The stations studied were identified as semiarid (annual ratio P∕ET0 between 0.2 and 0.5) according to the global aridity index developed by the United Nations Convention to Combat Desertification (UNEP, 1997). According to the climatic classification of Köppen (Kottek et al., 2006), this area presents a continental Mediterranean climate temperate with dry and temperate summer (type Csb). Temperature and precipitation of this site, based on 20 years, is presented in Table 1.
Table 1Monthly average of maximum temperature (Tmax), average temperature (Tavg), minimum temperature (Tmin) and precipitation (P). Study period from 1997 to 2017.

Due to high soil moisture conditions, ash is the dominant tree, forming large agroforestry systems (dehesas) that are used for pasture. These are ecosystems with high biodiversity.
2.4 HSL model
There is no doubt that NDVI time series from satellite sensors carry useful information, which can be used for characterizing seasonal dynamics of vegetation (Fensholt and Proud, 2012; Forkel et al., 2013). However, due to unfavorable atmospheric conditions during the data acquisition, the NDVI time-series curve often contains noise (Motohka et al., 2011; Park, 2013). Although most of the NDVI data products are temporally composited through the maximum value compositing (MVC) method (Holben, 1986) to retain relatively cloud-free data, residual noise still exists in the data, which will affect the accuracy of the NDVI value.
Therefore, usually it is necessary to reconstruct NDVI time series before extracting information from the noisy data. There are several techniques that have been applied to reduce noise and reconstruct NDVI series, and a summary of these can be found in Wei et al. (2016). In this study we applied a simple filtering method based on the hue–saturation–lightness color model inspired by the work presented by Tackenberg (2007).
HSL color model is a cylindrical representation of RGB (red–green–blue) points. Their components are hue (color type), saturation (level of color purity) and lightness (color luminosity). Hue is the angular component, and it is more intuitive for humans since it is directly related to the color wheel (see Fig. 2).
Saturation is the radial component and near-zero values indicate gray colors. Lightness is the axial radial versus axial component, zero lightness produces black and full lightness produces white.
The NDVI series are filtered using the following HSL criterion: NDVI values are valid if HSL saturation is greater than 0.15. The pixels that have gray colors correlate well with pasture areas covered by clouds or snow. In these cases, the NDVI values calculated in these pixels are incorrect. Using the above HSL criterion, all these NDVI values are eliminated. This type of filter based in HSL color space has been used on digital camera images monitoring vegetation phenology (Tackenberg, 2007; Crimmins and Crimmins, 2008; Graham et al., 2009). However, we have not found the use of this HSL criterion in the context of NDVI remote sensing images.
2.5 Maximum likelihood method
MLM estimates the set of parameters {α, β, μ, σ, …} for a specific statistical distribution that maximizes the likelihood function or the joint density function:
where x=(x1, …, xn) is the set of data, θ=(α, β, μ, σ, …) is the vector of parameters and f(xi; αβμσ, …) is the density function of the statistical model.
When maximization with respect to the vector of parameters is carried out, the estimated parameters (, , , , …) for the proposed statistical distribution are obtained (Larson, 1982). Important properties of these estimated parameters are consistency, efficiency and asymptotic normality.
In the case of a normal model, the estimated statistics μ and σ are defined by accurate expressions as follows:
where is the sample mean and is the sample standard deviation of the data set.
In this study we will apply MLM to estimate the parameters for four probability density functions (PDFs). In Table 2, a brief description is presented of these PDF candidates: normal, gamma, beta and generalized extreme value (GEV). To do so, the following MATLAB functions have been used: normfit, gamfit, betafit and gevfit.
2.6 Goodness of fit (χ2 test)
The χ2 test can be used to determine to what extent observed frequencies differ from frequencies expected for a specific statistical model. The most important points of the theory are briefly presented in Cochran (1952).
Let f(x, θ) be a theoretical density function of a random variable X which depends on parameters θ=(α, β, μ, σ, …) and let x1, …, xn be a sample of X grouped into k classes with ni data per class i.
Firstly, the following hypothesis is set: (H0) observed data fit theoretical distribution f(x, θ).
Then the test statistic is defined as
where ni is the number of data or observed frequency and (class i) is the expected frequency for class i. P(class i) is the theoretical interval probability defined for class i.
A level of significance is also set as
Finally, the following decision rule is applied: reject the theoretical distribution at significance level α if
where is a χ2 distribution with degrees of freedom (m is the number of parameters, k is the number of classes).
3.1 HSL filtering criterion
NDVI series (from 2002 to 2017) were obtained for each pixel of the study area using frequency bands provided by the MODIS product named MOD09A1. These series contain some irregular values that can skew the NDVI pattern. Therefore, the six series (6 pixels) were filtered using the HSL criterion.
MOD09A1 is a MODIS product that processes data to obtain the best observation in an 8 d period. However, it is possible that the result of this selection still presents some problems since the best selection is relative to the eight observations of the period. For example, if the eight observations, at 1 pixel, appear with clouds, shadow clouds or snow, the best selection still shows this problem.
As an example of the above, the NDVI series (10 years) of 1 pixel of the study area is shown in Fig. 3. On the top graph of Fig. 3 there are extremely low NDVI values in some dates. If these NDVI values are compared to neighboring values (8 d after or before) the high variation presented in such a short period is not plausible. This issue tells us that the MODIS sensor has not obtained a proper observation during this 8 d period (interval).
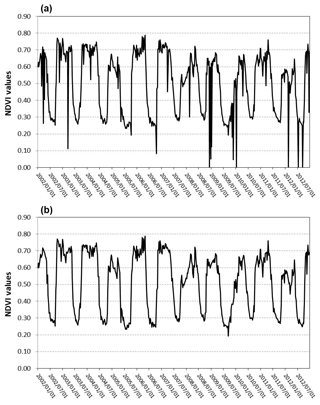
Figure 3HSL filtering criterion applied to a 10-year NDVI series. (a) shows the real NDVI series. (b) shows the HSL-filtered NDVI series.
The HSL criterion helps us to eliminate these incorrect NDVI values, since the filter is interpreting that these pixels still contains clouds or snow, i.e., pixels with low saturation (grayish colors).
Figure 3 shows that abrupt changes in the NDVI values, mainly observed during raining seasons such as autumn and winter, are efficiently eliminated. Not being a highly computationally demanding method is one of the main advantages of the HSL filtering method. Therefore, this method will allow us to obtain more robust NDVI values to be used in the statistical analysis.
3.2 Statistical analysis
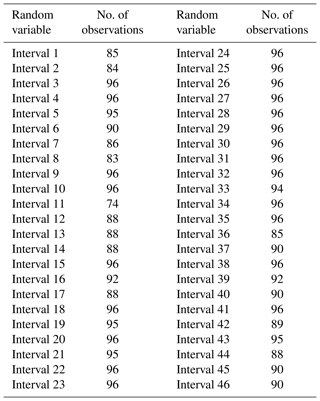
NDVI values were obtained consecutively every 8 d from MODIS starting at 1 January of every year, in such a way that 46 NDVI observations were extracted for each year. Therefore, it was possible to define 46 random variables (RVs) when all the years of this study were taken into account.
In Table 3, every RV (named “interval”) is shown together with the number of available NDVI observations. Each RV collects the observations coming from the 6 selected pixels; therefore the maximum number of observations per RV could be 6 pixels × 16 years = 96 observations. The starting intervals of each season are interval 45 (19 December) for winter, interval 11 (22 March) for spring, interval 23 (26 June) for summer and interval 34 (22 September) for autumn.
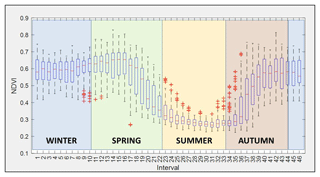
Figure 4Box plots of 46 random variables (RVs) are shown as well as the start and end reference of every season. The study period ranges from 2002 to 2017.
In Fig. 4, box plots of all RVs with a start and end reference of the astronomical seasons are shown. The typical evolution of the NDVI throughout a year can be seen together with the interquartile range.
The observed evolution of NDVI through the different seasons is typical of the pasture in this area. The summer presents the lowest mean values which begin to increase in autumn, achieving a maximum mean value of 0.60 or 0.65 during the beginning of spring. In the middle of the spring NDVIs decrease again, approaching the lowest mean value of 0.28 approximately in summer.
Taking into account these values, dense vegetation, in this study pasture, is found from the middle of October (interval 37) until the end of May (interval 19). It is in this period where the precipitation concentrates (see Table 1). During the summer, the NDVI mean values are lower than 0.3, corresponding with low precipitation and high temperatures.
Following the work of Escribano-Rodríguez et al. (2014), there is a relationship of pasture damage and a NDVI value around 0.40. Even if the authors point out that this value is highly variable depending on the location, we can see that the summer season in this case study is under this value (see Fig. 4). This can explain that insurances for damaged pasture usually do not apply during these dates due to the arid environment (BOE, 2013).
The statistical metric used in this study to assess the fit of the observed NDVI values with respect to the PDF candidates (normal, gamma, beta and GEV) was the Chi-square test (χ2 test). The following steps were carried out:
-
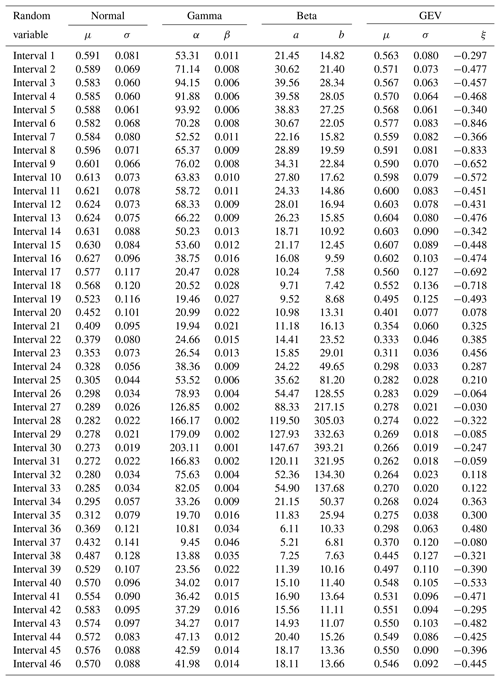
MLM was applied to model these 46 RVs. Parameters were calculated for the four PDF candidates (see Table 2).
-
To check the goodness of the fit of the PDF candidates, a Chi-square test (χ2 test) was applied from 7 to 14 classes meeting the requirement that each class have at least five observations. The level of significance (α) was fixed to 5 % for all the candidates.
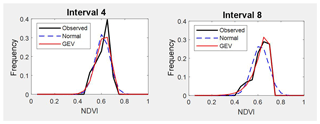
Figure 5Comparison between observed NDVI frequency, GEV and normal probability density functions (PDFs) on two different dates. Intervals 4 and 8 are examples for winter.
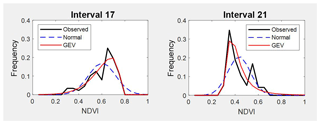
Figure 6Comparison between observed NDVI frequency, GEV and normal probability density functions on two different dates. Intervals 17 and 21 are examples for spring.
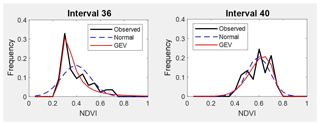
Figure 7Comparison between observed NDVI frequency, GEV and normal probability density functions on two different times. Intervals 36 and 41 are examples for autumn.
3.2.1 Maximum likelihood method
Table A1 shows the estimated parameters for each PDF and each interval calculated by the MLM. These parameters were used to compare the estimated PDF with the NDVI observed values on different times through the seasons. The following intervals are shown as examples of better GEV fit: interval 4 and 8 (for winter, see Fig. 5), interval 17 and 21 (for spring, see Fig. 6), and interval 36 and 40 (for autumn, see Fig. 7). In these plots, observed frequency is compared versus normal and GEV density distributions calculated by MLM.
During winter (see Fig. 5) the observed NDVI distribution presents negative skewness. Then, there is a higher frequency of high NDVI values corresponding with significant precipitation. During spring (see Fig. 6) an evolution in the skewness is observed passing from negative to positive, and so the lower NDVI values become more probable. Finally, during autumn (see Fig. 7) precipitation begins, the skewness passes from positive to negative values, and so higher NDVI values are possible again. We can observe that the normal distribution has no flexibility to follow this dynamic in the distributions for each time. This comparison is done in a sequential order for the whole of intervals in Figs. A1–A4.
3.2.2 χ2 test
Twelve intervals (from 23 to 34) corresponding to the months of July, August and September have been excluded in this analysis since these intervals fall into the dry season in the study area, which is normally not covered by any SIBI. Therefore, calculations were carried out over 34 intervals.
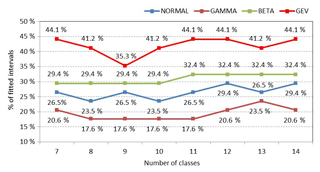
To assess the general goodness of fit, the number of intervals where the χ2 test was accepted (or failed to reject) were calculated for every PDF candidate. Then, the percentage of accepted intervals, over the total 34 intervals, was also calculated. Figure 8 shows the percentage of intervals that fit for every PDF candidate. The number of classes used in the χ2 test are represented on the x axis (from 7 to 14 classes).
4.1 Statistical context
Figure 8 indicates that GEV distributions explain more intervals (more than 40 % for the majority of the class analysis) than the normal, gamma or beta distributions. An important difference between the normal distribution and the PDFs used in this work is their skewness and kurtosis. Many of the observed NDVI distributions present a clear asymmetry and long tails in one or both sides that cause normal distributions not to be the optimal fit.
There is a relationship between seasons and the number of intervals that fit correctly. We found that GEV distributions explain intervals of spring and autumn better since their observed distributions are very asymmetric. On the other hand, we did not find an important difference in winter, since the observed distributions are mainly symmetric.
The more skewness and kurtosis depart from those of the normal distribution, the larger the errors affecting the insurance designed based on normal distributions (Turvey and Mclaurin, 2012). It is an expected result as pasture cultivation is quite different from the development of arable crops, where normal distributions in the NDVI values are more common. This high heterogeneity in time and space of NDVI estimated on pasture has been pointed out in several works (Martin-Sotoca et al., 2018). At the same time, the more different the observed NDVI frequency is from a normal distribution, the less representative the average is, and so the median becomes a more representative value.
4.2 Insurance context
The use of NDVI thresholds in a damaged pasture context was presented in the introduction section, being an example of using the insurance for damaged pasture in Spain (BOE, 2013). We have chosen this last insurance to compare the results between applying normal and GEV distribution methodologies. In this particular case the NDVI threshold (NDVIth) was calculated using the expression NDVI (where μ and σ are the average and standard deviation of NDVI distributions respectively, assuming the normal hypothesis).
The probability of being below NDVIth (using k=0.7, first damage level in the insurance) at every interval has been calculated assuming the normal hypothesis. As it was expected, this value is always 24.2 % (see third column in Table 4). The probability of being below NDVIth has also been calculated using GEV distributions obtained in this study. The probability obtained by GEV distributions is mostly lower than the normal distributions in spring, autumn and winter (see Table 4), which the working period of the insurance.
Table 4First column: time intervals of approximately 8 d throughout the year. Second column: NDVI thresholds (NDVIth) based on a normal distribution applying . Third column: percentages of area below the NDVIth when normal distributions are applied. Fourth column: percentages of area below the NDVIth when GEV distributions are applied. Fifth column: relative area error of GEV compared to the normal distribution.
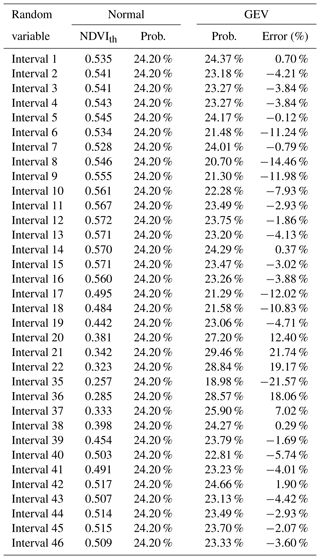
Observing where in time the highest relative errors in probabilities are (fifth column in Table 4), intervals corresponding to the end of winter, the second half of spring and the beginning of autumn present errors higher than 10 %. This could explain why it is in spring and autumn when more disagreements exist between farmers and insurance company in claims.
An alternative calculation can be the use of normal probability (24.2 %) to calculate new NDVIth based on GEV (see Table 5). It can be seen that the new NDVIth values obtained by GEV distributions are mostly higher than thresholds using normal distributions in spring, autumn and winter. Considering these results we find that damage thresholds calculated by GEV distributions are mostly above the ones calculated by normal distributions.
Table 5First column: time intervals of approximately 8 d throughout the year. Second column: NDVI thresholds (NDVIth) based on a normal distribution (normal) applying . Third column: NDVIth based on a GEV distribution (GEV) using 24.2 % as the area below the NDVIth. Fourth column: relative NDVIth error of GEV compared to the normal distribution.
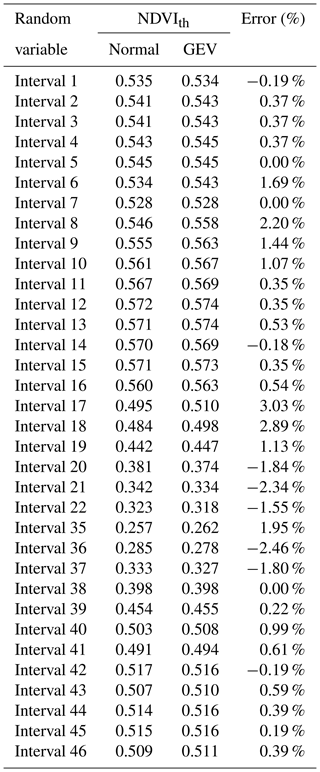
Again, intervals corresponding to the end of winter, the second half of spring and the beginning of autumn present NDVIth relative errors higher than 1 % in absolute values (fourth column in Table 5).
According to the results obtained in the study area using MLM and the χ2 test, it can be concluded that normal distributions are not a good fit to the NDVI observations, and GEV distributions provide a better approximation.
The difference between the normal and GEV assumption is more evident in the transition from winter to summer (spring), where NDVI values decrease, and then from summer to winter (autumn) presenting the opposite behavior of increasing NDVI values. In both periods, asymmetrical distributions were found – negative skewness for the spring transition and positive skewness for the autumn transition. During both periods the variability in precipitation and temperatures were higher in this location.
We have found differences if GEV assumption is selected instead of the normal one when defining damaged pasture thresholds (NDVIth). The use of these different assumptions should be taken into account in future insurance implementations due to the important consequences of supposing a damage event or not. We propose the use of quantiles in observed NDVI distributions instead of average and standard deviation, typically of normal distributions, to calculate new NDVIth.
Data will be made available upon an email request to the corresponding author.
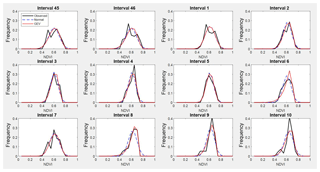
Figure A1Observed NDVI, GEV and normal probability density functions from interval 45 to interval 10 (from 19 December to 21 March) representing winter.
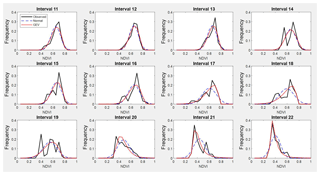
Figure A2Observed NDVI, GEV and normal probability density functions from interval 11 to interval 22 (from 22 March to 25 June) representing spring.
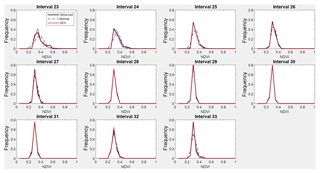
Figure A3Observed NDVI, GEV and normal probability density functions from interval 23 to interval 33 (from 26 June to 21 September) representing summer.
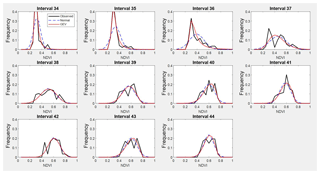
Figure A4Observed NDVI, GEV and normal PDFs from interval 34 to interval 44 (from 22 September to 18 December) representing autumn.
JMS developed the research idea and wrote the original draft of the manuscript, guided and supervised by ASR, RM, ND, IF and AMT. ASR contributed in the image filter design. AMT contributed with the imagery and statistical analysis. RM obtained the agro-meteorological and vegetation data for the classification of the area. ND and IF contributed in the introduction of index-based insurances and vegetation indexes, as well as in the setting of the vegetation index thresholds. AMT, ASR and RM reviewed and edited the manuscript for obtaining the final version.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Remote sensing, modelling-based hazard and risk assessment, and management of agro-forested ecosystems”. It is a result of the EGU General Assembly, Vienna, Austria, 8–13 April 2018.
This research has been partially supported by funding from MINECO under contract no. MTM2015-63914-P and CICYT PCIN-2014-080. The last author is grateful to the Comunidad de Madrid (Spain) and Structural Funds 2014–2020 (ERDF and ESF) for the financial support (project AGRISOST-CM S2018/BAA-4330) and EU project 821964 – BEACON.
This paper was edited by Anne Gobin and reviewed by three anonymous referees.
AEMET: OpenData. Sistema para la difusión y reutilización de la información de AEMET, available at: https://opendata.aemet.es/centrodedescargas/inicio (last access: 2 August 2019), 2017.
Al-Bakri, J. T. and Taylor, J. C.: Application of NOAA AVHRR for monitoring vegetation conditions and biomass in Jordan, J. Arid Environ, 54, 579–593, 2003.
Anyamba, A., and Tucker, C. J.: Historical perspective of AVHRR NDVI and vegetation drought monitoring, in: Remote Sensing of Drought: Innovative Monit Approaches, CRC Press/Taylor & Francis, Florida, USA, 23–50, 2012.
Bailey, S.: The Impact of Cash Transfers on Food Consumption in Humanitarian Settings: A review of evidence, Study for the Canadian Foodgrains Bank, Canadian Foodgrains Bank, Winnipeg, Canada, May 2013.
Bayarjargal, Y., Karnieli, A., Bayasgalan, M., Khudulmur, S., Gandush, C., and Tucker, C. J.: A comparative study of NOAA-AVHRR derived drought indices using change vector analysis, Remote Sens. Environ., 105, 9–22, 2006.
BOE – Boletin Oficial del Estado: 6638 – Orden AAA/1129/2013, No. 145, III, p-46077, Gobierno de España, Madrid, Spain, 2013.
Cochran, W. G.: The Chi-square Test of Goodness of Fit, Ann. Math. Stat., 23, 315–345, 1952.
Crimmins, M. A. and Crimmins, T. M.: Monitoring plant phenology using digital repeat photography, Environ. Manage., 41, 949–958, 2008.
Dalezios, N. R.: The Role of Remotely Sensed Vegetation Indices in Contemporary Agrometeorology, Invited paper in Honorary Special Volume in memory of late Prof. A. Flokas, Hellenic Meteorological Association, Athens, Greece, 33–44, 2013.
Dalezios, N. R., Blanta, A., Spyropoulos, N. V., and Tarquis, A. M.: Risk identification of agricultural drought for sustainable Agroecosystems, Nat. Hazards Earth Syst. Sci., 14, 2435–2448, https://doi.org/10.5194/nhess-14-2435-2014, 2014.
De Leeuw, J., Vrieling, A., Shee, A., Atzberger, C., Hadgu, K. M., Biradar, C. M., Humphrey Keah, H., and Turvey, C.: The Potential and Uptake of Remote Sensing in Insurance: A Review, Remote Sens., 6, 10888–10912, 2014.
Escribano Rodríguez, A., Díaz-Ambrona, J., Carlos, G. H., and Tarquis Alfonso, A. M.: Selection of vegetation indices to estimate pasture production in Dehesas, PASTOS, 44, 6–18, 2014.
Fensholt, R. and Proud, S. R.: Evaluation of earth observation based global long term vegetation trends - comparing GIMMS and MODIS global NDVI time series, Remote Sens. Environ., 119, 131–147, 2012.
Flynn, E. S.: Using NDVI as a pasture management tool, MS Thesis, University of Kentucky, Kentucky, 2006.
Forkel, M., Carvalhais, N., Verbesselt, J., Mahecha, M. D., Neigh, C. S., and Reichstein, M.: Trend change detection in NDVI time series: effects of inter-annual variability and methodology, Remote Sens., 5, 2113–2144, 2013.
Fuller, D. O.: Trends in NDVI time series and their relation to rangeland and crop production in Senegal, 1987–1993, Int. J. Remote Sens., 19, 2013–2018, 1998.
Gommes, R. and Kayitakire, F.: The challenges of index-based insurance for food security in developing countries, in: Proceedings, Technical Workshop, JRC, 2–3 May 2012, JRC-EC, Ispra, p. 276, 2013.
Gouveia, C., Trigo, R. M., and DaCamara, C. C.: Drought and vegetation stress monitoring in Portugal using satellite data, Nat. Hazards Earth Syst. Sci., 9, 185–195, https://doi.org/10.5194/nhess-9-185-2009, 2009.
Goward, S. N., Tucker, C. J., and Dye, D.G.: North-American vegetation patterns observed with the NOAA-7 advanced very high-resolution radiometer, Vegetation, 64, 3–14, 1985.
Graham, E. A., Yuen, E. M., Robertson, G. F., Kaiser, W. J., Hamilton, M. P., and Rundel, P. W.: Budburst and leaf area expansion measured with a novel mobile camera system and simple color thresholding, Environ. Exp. Bot., 65, 238–244, 2009.
Hobbs, T. J.: The use of NOAA-AVHRR NDVI data to assess herbage production in the arid rangelands of central Australia, Int. J. Remote Sens., 16, 1289–1302, 1995.
Holben, B. N.: Characteristics of maximum-value composite images from temporal AVHRR data, Int. J. Remote Sens., 7, 1417–1434, 1986.
Kottek, M., Grieser, J., Beck, C., Rudolf, B., and Rubel, F.: World Map of the Köppen-Geiger climate classification updated, Meteorol. Z., 15, 259–263, 2006.
Kundu, A., Dwivedi, S., and Dutta, D.: Monitoring the vegetation health over India during contrasting monsoon years using satellite remote sensing indices, Arab. J. Geosci., 9, 144, 2016.
Larson, H. J.: Introduction to Probability Theory and Statistical Inference, 3rd Edn., John Wiley and Sons, New York, 1982.
Leblois, A.: Weather index-based insurance in a cash crop regulated sector: ex ante evaluation for cotton producers in Cameroon, in: Paper presented at the JRC/IRI workshop on The Challenges of Index-Based Insurance for Food Security in Developing Countries, 2–3 May 2012, Ispra, 2012.
Li, R., Tsunekawa, A., and Tsubo, M.: Index-based assessment of agricultural drought in a semi-arid region of Inner Mongolia, China, J. Arid Land, 6, 3–15, 2014.
Lovejoy, S., Tarquis, A. M., Gaonac'h, H., and Schertzer, D.: Single and Multiscale remote sensing techniques, multifractals and MODIS derived vegetation and soil moisture, Vadose Zone J., 7, 533–546, 2008.
LP DAAC – Land Processes Distributed Active Archive Center: Surface Reflectance 8-Day L3 Global 500 m, NASA and USGS, available at: https://lpdaac.usgs.gov/products/mod09a1v006/ (last access: 2 August 2019), 2014.
Maples, J. G., Brorsen, B. W., and Biermaches, J. T.: The rainfall Index Annual Forage pilot program as a risk management tool for cool-season forage, J. Agr. Appl Econ, 48, 29–51, 2016.
Martin-Sotoca, J. J., Saa-Requejo, A., Orondo J. B., and Tarquis, A. M.: Singularity maps applied to a vegetation index, Bio. Eng., 168, 42–53, 2018.
Motohka, T., Nasahara, K. N., Murakami, K., and Nagai, S.: Evaluation of sub-pixel cloud noises on MODIS daily spectral indices based on in situ measurements, Remote Sens., 3, 1644–1662, 2011.
Nanzad, L., Zhang, J., Tuvdendorj, B., Nabil, M., Zhang, S., and Bai, Y.: NDVI anomaly for drought monitoring and its correlation with climate factors over Mongolia from 2000 to 2016, J. Arid Environ., 164, 69–77, 2019.
Niemeyer, S.: New drought indices, in: First Int. Conf. on Drought Management: Scientific and Technological Innovations, Zaragoza, Spain, Joint Research Centre of the European Commission, available at: http://projects.iamz.ciheam.org/medroplan/zaragoza2008/Sequia2008/Session3/S.Niemeyer.pdf (last access: 2 August 2019), 2008.
Ortega-Farias, S., Ortega-Salazar, S., Poblete, T., Kilic, A., Allen, R., Poblete-Echeverría, C., Ahumada-Orellana, L., Zuñiga, M., and Sepúlveda, D.: Estimation of Energy Balance Components over a Drip-Irrigated Olive Orchard Using Thermal and Multispectral Cameras Placed on a Helicopter-Based Unmanned Aerial Vehicle (UAV), Remote Sens., 8, 638, 2016.
Park, S.: Cloud and cloud shadow effects on the MODIS vegetation index composites of the Korean Peninsula, Int. J. Remote Sens., 34, 1234–1247, 2013.
Peters, A. J., Walter-Shea, E. A., Ji, L., Vina, A., Hayes, M., and Svoboda, M. D.: Drought monitoring with NDVI-Based Standardized Vegetation Index, Photogram. Eng. Remote Sens., 68, 71–75, 2002.
Rao, K. N.: Index based Crop Insurance, Agric. Agric. Sci. Proc., 1, 193–203, 2010.
Roumiguié, A., Jacquin, A., Sigel, G., Poilvé, H., Lepoivre, B., and Hagolle, O.: Development of an index-based insurance product: validation of a forage production index derived from medium spatial resolution fCover time series, GIScience Remote Sens., 52, 94–113, 2015.
Roumiguié, A., Sigel, G., Poilvé, H., Bouchard, B., Vrieling, A., and Jacquin, A.: Insuring forage through satellites: testing alternative indices against grassland production estimates for France, Int. J. Remote Sens., 38, 1912–1939, 2017.
Tackenberg, O.: A New Method for Non-destructive Measurement of Biomass, Growth Rates, Vertical Biomass Distribution and Dry Matter Content Based on Digital Image Analysis, Ann. Bot., 99, 777–783, 2007.
Turvey, C. G. and Mclaurin, M. K.: Applicability of the Normalized Difference Vegetation Index (NDVI) in Index-Based Crop Insurance Design, Am. Meorol. Soc., 4, 271–284, 2012.
UNEP Word Atlas of Desertification: Second Ed. United Nations Enviroment Programe, Nairobi, 1997.
USDA – US Department of Agriculture, Federal Crop Insurance Corporation, Risk Management Agency: Rainfall Index Plan Annual Forage Crop Provisions, 16-RI-AF, available at: http://www.rma.usda.gov/policies/ri-vi/2015/16riaf.pdf 2013, last access: 1 March 2018.
Wei, W., Wu, W., Li, Z., Yang, P., and Qingbo Zhou, Q.: Selecting the Optimal NDVI Time-Series Reconstruction Technique for Crop Phenology Detection, Intell. Autom. Soft. Co., 22, 237–247, 2016.