the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Brief communication: Modulation instability of internal waves in a smoothly stratified shallow fluid with a constant buoyancy frequency
Kwok Wing Chow
Hiu Ning Chan
Roger H. J. Grimshaw
Unexpectedly large displacements in the interior of the oceans are studied through the dynamics of packets of internal waves, where the evolution of these displacements is governed by the nonlinear Schrödinger equation. In cases with a constant buoyancy frequency, analytical treatment can be performed. While modulation instability in surface wave packets only arises for sufficiently deep water, “rogue” internal waves may occur in shallow water and intermediate depth regimes. A dependence on the stratification parameter and the choice of internal modes can be demonstrated explicitly. The spontaneous generation of rogue waves is tested here via numerical simulation.
Rogue waves are unexpectedly large displacements from equilibrium positions or otherwise tranquil configurations. Oceanic rogue waves on the sea surface obviously pose immense risk to marine vessels and offshore structures (Dysthe et al., 2008). As these waves were observed in optical waveguides, studies of such extreme and rare events have been actively pursued in many fields of science and engineering (Onorato et al., 2013). Within the realm of oceanic hydrodynamics, observation of rogue waves in coastal regions has been recorded (Nikolkina and Didenkulova, 2011; O'Brien et al., 2018). Nearly all experimental and theoretical studies in the literature of rogue waves in fluids focus on surface waves. Our aim here is to investigate a similar scenario for internal waves. Internal waves play critical roles in the transport of heat, momentum and energy in the oceans, and breaking of such waves may have an impact on circulation (Pedlosky, 1987). There is a substantial literature on the observations and theories of large-amplitude internal waves in shallow water (Stanton and Ostrovsky, 1998). Many studies concentrate on solitary waves in long-wave situations employing the Korteweg–de Vries equation (Holloway et al., 1997) but not on the highly transient modes with the potential for abrupt growth. In terms of relevance in other fields of physics and engineering, the actual derivation of the governing equations may dictate the regime of input parameter values necessary for rogue waves to occur.
Theoretically, the propagation of weakly nonlinear, weakly dispersive narrowband wave packets is governed by the nonlinear Schrödinger equation, where the dynamics are dictated by the competing effects of second-order dispersion and cubic nonlinearity (Zakharov, 1968; Ablowitz and Segur, 1979). Modulation instability of plane waves and rogue waves can then occur only if dispersion and cubic nonlinearity are of the same sign. For surface wave packets on a fluid of finite depth, rogue modes can emerge for kh>1.363, where k is the wavenumber of the carrier wave packet and h is the water depth. Hence, conventional understanding is that such rogue waves can only occur if the water depth is sufficiently large.
Other fluid physics phenomena have also been considered, such as the effects of rotation (Whitfield and Johnson, 2015) or the presence of a shear current, an opposing current (Onorato et al., 2011; Toffoli et al., 2013a; Liao et al., 2017) or an oblique perturbation (Toffoli et al., 2013b). While such considerations may change the numerical value of the threshold (1.363) and extend the instability region, the requirement of water of sufficiently large depth is probably unaffected. For wave packets of large wavelengths, dynamical models associated with the shallow water regime have been employed (Didenkulova and Pelinovsky, 2011, 2016), such as the well-known Korteweg–de Vries and Kadomtsev–Petviashvili types of equations (Grimshaw et al., 2010, 2015; Pelinovsky et al., 2000; Talipova et al., 2011), which may also lead to modulation instability under several special circumstances.
The goal here is to establish another class of rogue-wave occurrence through the effects of density stratification, namely, internal waves in the interior of the oceans. Internal waves in general display more complex dynamical features than their surface counterparts. As an illustrative example, a given density profile may allow many internal modes characterized by the number of nodes in the vertical structures. This family of allowed states will be generically represented in this paper by an integer n (referred to here as the mode number). There is an extensive literature on large-amplitude internal solitary waves that are spatially localized pulses essentially propagating without change of form (Grimshaw et al., 2004; Osborne, 2010). Our focus here is on internal rogue waves that are modeled as wave pulses localized in both space and time. The asymptotic multiple scale expansions for internal wave packets under the Boussinesq approximation also yield the nonlinear Schrödinger equation (Grimshaw, 1977, 1981; Liu and Benney, 1981). When the buoyancy frequency is constant, modulation instability in one horizontal space dimension will only occur for , where the fluid is confined between rigid walls that are distance h apart, n is the vertical mode number of the internal wave and the critical wavenumber kc is given by the following equation (Liu et al., 2018):
For a wave packet associated with the first internal mode (n=1), modulation instability or a rogue wave can occur with the carrier wavenumber k and shallow fluid of depth h in the range of kh<0.766π or 2.406.
For a basin depth (h) of, for example, 500 m, the critical wavelength (λc) is as follows:
and the ranges of “shallow” and “intermediate” depths are covered (Table 1).
The important point is not just a difference in the numerical value of the cutoff but that rogue waves now occur for water depths lower than a certain threshold. Our contribution is to extend this result. The nonlinear focusing mechanism of internal rogue waves is (i) determined by an estimation of the growth rate of modulation instability and (ii) elucidated by a numerical simulation of the emergence of rogue modes with the optimal modulation instability growth rate as the initial condition.
2.1 Nonlinear Schrödinger theory for stratified shear flows
The dynamics of small-amplitude (linear) waves in a stratified shear flow with the Boussinesq approximation is governed by the Taylor–Goldstein equation (ϕ(y) is the vertical structure, k is the wavenumber, c is the phase speed and U(y) is the shear current):
where N is the Brunt–Väisälä frequency (or the “buoyancy frequency”; is the background density profile) by
The evolution of weakly nonlinear, weakly dispersive wave packets is described by the nonlinear Schrödinger equation for the complex-valued wave envelope S, obtained through a multi-scale asymptotic expansion, which involves calculating the induced mean flow and second harmonic (β and γ being parameters determined from the density and current profiles):
where τ is the slow timescale, ξ is the group velocity (cg) coordinate and ε is a small amplitude parameter.
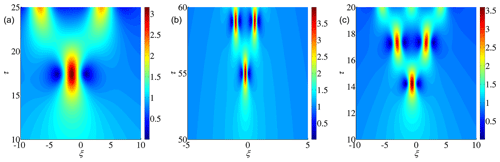
Figure 1The emergence of rogue-wave modes from a background continuous wave perturbed by a long-wavelength unstable mode. Larger baseband gain implies a smaller time is required for the rogue-wave modes to emerge. (a) For N0=2, h=4, k=0.5, n=1, r=0.2 and baseband instability growth rate = 0.868, a rogue wave emerges at τ≈17. (b) For N0=2, h=1, k=0.5, n=1, r=0.2 and baseband instability growth rate = 0.193, a longer time is required for the emergence of a rogue wave in a shallower fluid (τ≈55). (c) For N0=1, h=4, k=0.5, n=1, r=0.2 and baseband instability growth rate = 0.868, a rogue wave emerges at about the same time (τ≈14) as compared to the case with a higher buoyancy frequency N0=2. In all cases, the amplitude of the background continuous wave (A0) is taken as 1.
2.2 Constant buoyancy frequency
For the simple case of constant buoyancy frequency N0, the formulations simplify considerably in the absence of shear flow (U(y)=0). The linear theory Eq. (2) yields simple solutions for the mode number n:
with the dispersion relation, phase velocity (c) and group velocity (cg) given by
The subsequent nonlinear analysis yields the coefficients of the nonlinear Schrödinger equation in explicit forms:
A plane wave solution for Eq. (4) (or, physically, a continuous wave background of amplitude A0) is as follows:
Small disturbances with modal dependence exp [i(rξ−Ωτ)] will exhibit modulation instability if
- a.
is negative, i.e., for βγ>0; calculations using Eqs. (6) and (7) lead to (Eq. 1);
- b.
the maximum growth rate is (imaginary part of for a special wavenumber given by ;
- c.
the growth rate for long-wavelength disturbance is for r→0.
In terms of significance in oceanography, the constraint does not depend on the constant buoyancy frequency N0. However, it does depend on the mode number (n) of the internal wave, with the higher-order modes permitting a large range of carrier envelope wavenumbers and fluid depths for rogue waves to occur. An analysis in the long-wave regime of this Taylor–Goldstein formulation would in principle recover the previous results related to the Korteweg–de Vries and Gardner equations, and details will be reported in the future.
An intensively debated issue in the study of rogue waves through a deterministic approach is the proper initial condition that may generate or favor the occurrence of such large-amplitude disturbances. Modulation instability refers to the growth of a small disturbance in a system due to the interplay between dispersive and nonlinear effects (Craik, 1984), and here we examine this instability by solving the nonlinear Schrödinger equation (Eq. 4) numerically. One suggestion is the role played by long-wavelength modes associated with modulation instability (also known as “baseband instability”; Baronio et al., 2015). To examine this effect and to clarify the role of stratification as well as the choice of internal wave modes, numerical simulations are performed where baseband modes with the scaled modulation instability growth rate on a plane wave background and, for example, 5% amplitude are selected as the initial condition (Chan and Chow, 2017; Chan et al., 2018):
where A0 is the amplitude parameter defined by Eq. (8) and r is the wavenumber of the baseband mode.
This choice of a preferred modulation instability mode as the initial condition is different from other approaches in the literature, such as one using random noise. A pseudospectral method with a fourth-order Runge–Kutta scheme for progressing through time is applied to solve the nonlinear Schrödinger equation (Eq. 4) numerically. When the wavenumber r of the disturbance is small, corresponding to a baseband mode, a rogue wave can be generated from the plane wave background (Fig. 1). Physically this spontaneous growth of disturbance due to modulation instability is closely associated with the “focusing” of energy and thus the formation of rogue waves.
The growth rate of the baseband mode is a crucial factor of rogue-wave generation. A stronger baseband growth rate will trigger a rogue wave within a shorter period of time. From Eqs. (6) and (7), the baseband growth rate (2βγ)1∕2A0 increases as the depth h or wavenumber k increases (Fig. 2), but this growth rate decreases as the mode number n increases. However, this baseband rate is independent of the buoyancy frequency N0. Numerical simulations were performed with parameter values appropriate for application to fluid mechanics. The concrete numerical values of the growth rates in a laboratory frame of reference (time t) can be estimated from definitions used in Eq. (4), i.e., τ=ε2t and the small amplitude parameter ε actually employed.
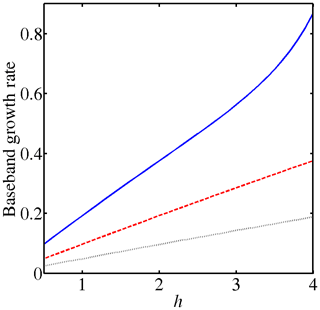
Figure 2The baseband growth rate increases as the fluid depth h increases: N0=2, k=0.5, n=1 (solid blue line); N0=2, k=0.5, n=2 (dashed red line); and N0=2, k=0.25, n=1 (dotted black line).
Figure 1 shows that rogue waves can emerge sooner when the fluid is deeper. Remarkably, this implies that baseband instability is stronger when the system is closer to the singular limit where the cubic nonlinearity changes sign. On the other hand, the degree of the background density stratification creates only a minor effect on the baseband mode. Apart from choosing a preferred baseband mode, another perspective taken in the literature is to select a random field as the initial condition. For the present nonlinear Schrödinger equation, “rogue-wave-like” entities would then emerge as well (Akhmediev et al., 2009).
An analytically tractable model for packets of internal waves was studied here through four input parameters, h (fluid depth), k (wavenumber of the carrier envelope packet), N0 (buoyancy frequency) and n (mode number of the internal wave), with only h and k relevant for surface waves. For internal waves, modulation instabilities and rogue waves may now arise for the shallow water and intermediate depth regimes if N0 is constant. With knowledge of baseband instability and supplemented by computer simulations, the nonlinear focusing mechanism of rogue waves is assessed. Remarkably the constant buoyancy frequency may not play a critical role in the existence condition in terms of focusing, but the mode number of the internal wave does. For breathers or other pulsating modes, this buoyancy frequency parameter will enter the focusing mechanism consideration and further analytical and computational studies will be valuable (Sergeeva et al., 2014). In the next phase of this research effort, contrasts and similarities with surface waves should also be pursued, where a directional field or opposing current can provide rogue-wave generation mechanisms beyond the well-established criterion of kh>1.363. Such effects of shear currents and comparisons with experimental and field data will be taken up in future studies (Onorato et al., 2011; Toffoli et al., 2013a, b). Density profiles with variable buoyancy frequency will also be examined in the future. Besides their relevance to transport phenomena, internal waves have a significant connection with underwater acoustics (Apel et al., 2007; Zhou et al., 1991) and abnormally large internal rogue waves may have physical implications for those aspects.
No data sets were used in this article.
KWC initiated the idea of studying and comparing the connections between modulation instability and rogue waves for internal versus surface modes. RHJG advised on the literature on internal waves and refined the formulation as well as the writing style. HNC performed the numerical simulations.
The authors declare that they have no conflict of interest.
Partial financial support has been provided by the Research Grants Council (contracts HKU17200815 and HKU17200718).
This paper was edited by Ira Didenkulova and reviewed by Efim Pelinovsky, Yury Stepanyants and one anonymous referee.
Ablowitz, M. J. and Segur, H.: On the evolution of packets of water waves, J. Fluid Mech., 92, 691–715, 1979.
Akhmediev, N., Ankiewicz, A., and Soto-Crespo, J. M.: Rogue waves and rational solutions of the nonlinear Schrödinger equation, Phys. Rev. E, 80, 026601, https://doi.org/10.1103/PhysRevE.80.026601, 2009.
Apel, J. R., Ostrovsky, L. A., Stepanyants, Y. A., and Lynch, J. F.: Internal solitons in the ocean and their effect on underwater sound, J. Acoust. Soc. Am., 121, 695–722, 2007.
Baronio, F., Chen, S., Grelu, P., Wabnitz, S., and Conforti, M.: Baseband modulation instability as the origin of rogue waves, Phys. Rev. A, 91, 033804, https://doi.org/10.1103/PhysRevA.91.033804, 2015.
Chan, H. N. and Chow, K. W.: Rogue waves for an alternative system of coupled Hirota equations: Structural robustness and modulation instabilities, Stud. Appl. Math., 139, 78–103, 2017.
Chan, H. N., Grimshaw, R. H. J., and Chow, K. W.: Modeling internal rogue waves in a long wave-short wave resonance framework, Phys. Rev. Fluids, 3, 124801, https://doi.org/10.1103/PhysRevFluids.3.124801, 2018.
Craik, A. D. D.: Wave Interactions and Fluid Flows, Cambridge University Press, Cambridge, 1984.
Didenkulova, I. and Pelinovsky, E.: Rogue wave in nonlinear hyperbolic systems (shallow-water framework), Nonlinearity, 24, R1–R18, 2011.
Didenkulova, I. and Pelinovsky, E.: On shallow water rogue wave formation in strongly inhomogeneous channels, J. Phys. A, 49, 194001, https://doi.org/10.1088/1751-8113/49/19/194001, 2016.
Dysthe, K., Krogstad, H. E., and Müller, P.: Oceanic rogue waves, Annu. Rev. Fluid Mech., 40, 287–310, 2008.
Grimshaw, R.: Modulation of an internal gravity wave packet in a stratified shear flow, Wave Motion, 3, 81–103, 1981.
Grimshaw, R., Pelinovsky, E., Talipova, T., and Kurkin, A.: Simulation of the transformation of internal solitary waves on oceanic shelves, J. Phys. Oceanogr., 34, 2774–2779, 2004.
Grimshaw, R., Pelinovsky, E., Taipova, T., and Sergeeva, A.: Rogue internal waves in the ocean: Long wave model, Eur. Phys. J. Spec. Top., 185, 195–208, 2010.
Grimshaw, R., Chow, K. W., and Chan, H. N.: Modulational instability and rogue waves in shallow water models, in: New Approaches to Nonlinear Waves, edited by: Tobisch, E., Lect. Notes Phys., 908, 135–149, 2015.
Grimshaw, R. H. J.: The modulation of an internal gravity-wave packet, and the resonance with the mean motion, Stud. Appl. Math., 56, 241–266, 1977.
Holloway, P. E., Pelinovsky, E., Talipova, T., and Barnes, B.: A nonlinear model of internal tide transformation on the Australian North West Shelf, J. Phys. Oceanogr., 27, 871–896, 1997.
Liao, B., Dong, G., Ma, Y., and Gao, J. L.: Linear-shear-current modified Schrödinger equation for gravity waves in finite water depth, Phys. Rev. E, 96, 043111, https://doi.org/10.1103/PhysRevE.96.043111, 2017.
Liu, A. K. and Benney, D. J.: The evolution of nonlinear wave trains in stratified shear flows, Stud. Appl. Math., 64, 247–269, 1981.
Liu, T. Y., Chan, H. N., Grimshaw, R. H. J., and Chow, K. W.: Internal rogue waves in stratified flows and the dynamics of wave packets, Nonlin. Anal. Real World Appl., 44, 449–464, 2018.
Nikolkina, I. and Didenkulova, I.: Rogue waves in 2006–2010, Nat. Hazards Earth Syst. Sci., 11, 2913–2924, https://doi.org/10.5194/nhess-11-2913-2011, 2011.
O'Brien, L., Renzi, E., Dudley, J. M., Clancy, C., and Dias, F.: Catalogue of extreme wave events in Ireland: revised and updated for 14 680 BP to 2017, Nat. Hazards Earth Syst. Sci., 18, 729–758, https://doi.org/10.5194/nhess-18-729-2018, 2018.
Onorato, M., Proment, D., and Toffoli, A.: Triggering rogue waves in opposing currents, Phys. Rev. Lett., 107, 184502, https://doi.org/10.1103/PhysRevLett.107.184502, 2011.
Onorato, M., Residori, S., Bortolozzo, U., Montina, A., and Arecchi, F. T.: Rogue waves and their generating mechanisms in different physical contexts, Phys. Rep., 528, 47–89, 2013.
Osborne, A. R.: Nonlinear Ocean Waves and the Inverse Scattering Transform, Academic Press, Burlington, 2010.
Pedlosky, J.: Geophysical Fluid Dynamics, Springer-Verlag, New York, 1987.
Pelinovsky, E., Talipova, T., and Kharif, Ch.: Nonlinear-dispersive mechanism of the freak wave formation in shallow water, Physica D, 147, 83–94, 2000.
Sergeeva, A., Slunyaev, A., Pelinovsky, E., Talipova, T., and Doong, D.-J.: Numerical modeling of rogue waves in coastal waters, Nat. Hazards Earth Syst. Sci., 14, 861–870, https://doi.org/10.5194/nhess-14-861-2014, 2014.
Stanton, T. P. and Ostrovsky, L. A.: Observations of highly nonlinear internal solitons over the Continental Shelf, Geophys. Res. Lett., 25, 2695–2698, 1998.
Talipova, T. G., Pelinovsky, E. N., and Kharif, C.: Modulation instability of long internal waves with moderate amplitudes in a stratified horizontally inhomogeneous ocean, JETP Lett., 94, 182–186, 2011.
Toffoli, A., Waseda, T., Houtani, H., Kinoshita, T., Collins, K., Proment, D., and Onorato, M.: Excitation of rogue waves in a variable medium: An experimental study on the interaction of water waves and currents, Phys. Rev. E, 87, 051201(R), https://doi.org/10.1103/PhysRevE.87.051201 2013a.
Toffoli, A., Fernandez, L., Monbaliu, J., Benoit, M., Gagnaire-Renou, E., Lefèvre, J. M., Cavaleri, L., Proment, D., Pakozdi, C., Stansberg, C. T., Waseda, T., and Onorato, M.: Experimental evidence of the modulation of a plane wave to oblique perturbations and generation of rogue waves in finite water depth, Phys. Fluids, 25, 091701, https://doi.org/10.1063/1.4821810, 2013b.
Whitfield, A. J. and Johnson, E. R.: Modulational instability of co-propagating internal wavetrains under rotation, Chaos, 25, 023109, https://doi.org/10.1063/1.4908571, 2015.
Zakharov, V. E.: Stability of periodic waves of finite amplitude on the surface of a deep fluid, J. Appl. Mech. Tech. Phys., 9, 190–194, 1968.
Zhou, J. X., Zhang, X. Z., and Rogers, P. H.: Resonant interaction of sound wave with internal solitons in the coastal zone, J. Acoust. Soc. Am., 90, 2042–2054, 1991.






