the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Exposure-based risk assessment and emergency management associated with the fallout of large clasts at Mount Etna
Sara Osman
Eduardo Rossi
Costanza Bonadonna
Corine Frischknecht
Daniele Andronico
Raffaello Cioni
Simona Scollo
Fallout of ballistic blocks and bombs ejected from eruptive vents represents a well-known hazard in areas proximal to volcanoes (mostly <5 km from the vent). However, fallout of large clasts sedimenting from plume margins that extend to medial areas and have the potential to produce severe injuries to people and cause damage to infrastructure, is often overlooked. Recent eruptive events at Mount Etna (Italy) provide a clear example where large-clast fallout from plume margins (>5 cm) has posed a real threat both to the many visitors reaching the summit area and to local infrastructure, and, therefore, has been selected as a case study. To quantify this hazard, a new particle sedimentation model was calibrated with field data and then used for probabilistic hazard assessments. For a fully probabilistic scenario the hazard zone covered 72 km2 and included some 125 km of paths and roads, as well as 15 buildings. Evacuation on foot to a safe area was estimated at almost 4 h, but this could be reduced to less than 3 h if two shelters were provided. Our results show the importance of integrating probabilistic hazard analysis of large-clast fallout within effective strategies of risk management and reduction, especially in the case of volcanoes where visitors can reach the summit areas.
- Article
(16947 KB) -
Supplement
(3324 KB) - BibTeX
- EndNote
Tephra sedimentation associated with explosive volcanic eruptions includes particles ranging from ash (<2 mm) to lapilli (2–64 mm) and blocks (>64 mm). Ash mostly falls out from the umbrella cloud and the top of buoyant plumes and, unless aggregated, can reach distances of hundreds of kilometres from the vent. Lapilli mostly fall out from the plume margins within tens of kilometres from the vent, while blocks and bombs ejected directly from the vent can fall ballistically within a few kilometres or be entrained within the plume and sediment from its margins together with the coarsest lapilli (e.g. Bursik et al., 1992). The hazard associated with the sedimentation of ash and fine to medium lapilli (i.e. particles <16 mm) and with ballistic blocks has already been analysed and discussed in many studies (e.g. Biass et al., 2014, 2016a; Fitzgerald et al., 2014; Costa et al., 2009). However, the hazard associated with the sedimentation of coarse lapilli, blocks and bombs from the convective region of eruptive plumes (i.e. particles >16 mm; hereon defined as “large clasts”) has never been characterized. The risk associated with the sedimentation of large clasts from plume margins is more localized than for ash and fine to medium lapilli, where the area affected can extend over hundreds of kilometres and the impact can be felt across several economic sectors, including agriculture and transport (Jenkins et al., 2015). However, the physical impact associated with ash and lapilli is rarely dangerous for people, with the exception of eye irritation and long-term respiratory health issues (e.g. Horwell and Baxter, 2006). The impact area associated with the sedimentation of large clasts from plume margins is, however, potentially much larger than the area at risk of ballistic impact, which extends no more than 5 km from the vent (e.g. Bertin, 2017; Biass et al., 2016a; Fitzgerald et al., 2014). In fact, for small explosive eruptions (e.g. large lava fountains and small Vulcanian events), ballistic blocks are confined in very proximal areas (1–2 km from vent) (Calvari and Pinkerton, 2002), but large clasts can fall out some 10 km from the eruptive vent (Andronico et al., 2015, 2008), and this poses a particular risk at Mount Etna, where many people visit the summit area throughout the year. This also implies a risk of damage to infrastructure, including buildings and roads (e.g. Andronico et al., 2015; Wardman et al., 2012). Impact from large clasts (up to tens of centimetres) is particularly evident for small explosions that do not generate thick and widely dispersed tephra deposits, but it has also been reported for higher-intensity eruptions (e.g. the Vesuvius 79 CE, 472 CE, 1631 and 1906 eruptions: Cioni et al., 1992; Barsotti et al., 2015; Rosi et al., 1993; Sulpizio et al., 2005; and the Soufrière Saint Vincent 1902 eruption: Zuccaro et al., 2015). It is therefore important to assess the hazard models and probabilistic strategies.
As an example, we present the assessment of the hazard associated with the sedimentation of 5 cm clasts from lava-fountain-fed plumes at Mount Etna using the sedimentation model of Rossi et al. (2019). Explosive activity occurs frequently at the summit craters of Mount Etna, often consisting of Strombolian eruptions and lava fountains (e.g. Andronico et al., 2015; Corsaro et al., 2017; De Beni et al., 2015; Vulpiani et al., 2016). Tephra fallout is a well-documented hazard from these explosive eruptions (e.g. Donnadieu et al., 2016; Scollo et al., 2013), and proximal to the vent there is a high risk of injury to people and damage to infrastructure both from large clasts sedimented from the eruptive plume and from ballistic projectiles (Andronico et al., 2015; Calvari and Pinkerton, 2002). Results provide an opportunity to also assess the associated risk to infrastructure and consider emergency management (i.e. analysis of time required for people to reach a safe area based on a dedicated US Geological Survey (USGS) modelling tool; Jones et al., 2014). Validations of the model with Etna observations, model parameters and both eruptive and atmospheric parameters are described in Appendices A, B and C, respectively. In addition, data on historical activity at Mount Etna (Table S1), wind analysis (Figs. S1–S6), model sensitivity analysis (Figs. S7–S10), and additional hazard and evacuation-time analyses (Figs. S11–S14) are presented in the Supplement.
Lava-fountain-fed plumes at Mount Etna
Explosive eruptions at Mount Etna often take the form of lava fountains, when jets of lava reach heights ranging from a few tens to several hundreds of metres, and many generate ash plumes that can rise up to 15 km above sea level (a.s.l.) (Andronico et al., 2015, and references therein). More than 200 such events have occurred in the past 20 years (Andronico et al., 2015). High-intensity lava fountains are often short-lived but they can be extremely hazardous when large clasts are sedimented out proximal to the vent (Andronico et al., 2015). Some details of lava fountains since 1998 have been published and are listed in Table S1. In order to explore the variability of lava fountain events during which large clasts sedimented out from plume margins, two reference events have been considered for which data on clast type and dispersal are available.
A sequence of eight eruptive events occurred between October and December 2013 at the New Southeast Crater (NSEC). The paroxysm of 23 November 2013 was unusually explosive although the total erupted dense-rock equivalent (DRE) volume was similar to previous events ( m3; Bonaccorso et al., 2014). A lava fountain from 09:30 to 10:10 UTC reached a height of around 1 km above the vent (Andronico et al., 2015) and large scoria clasts damaged cars at Rifugio Citelli, around 5 km from the crater (shown in Fig. 1). Large clasts were sedimented from the rising plume, with the average diameter of scoria collected near Rifugio Citelli being over 10 cm (Andronico et al., 2015).
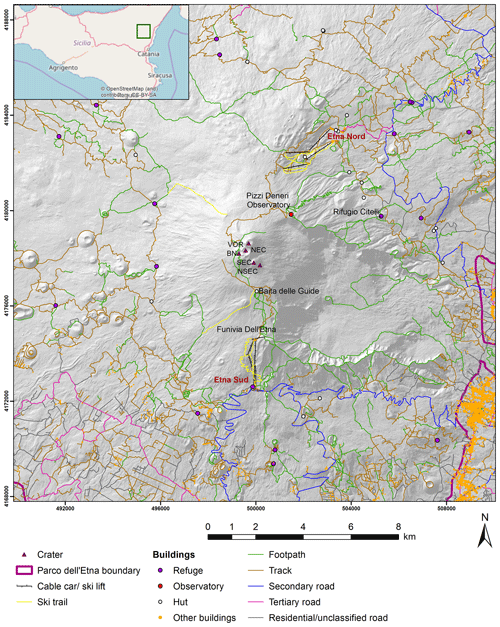
Figure 1Infrastructure within 10 km of the summit area of Mount Etna (data from OpenStreetMap Foundation, 2017a, b). BN: Bocca Nuova; NEC: Northeast Crater; NSEC: New Southeast Crater; SEC: Southeast Crater; VOR: Voragine.
Deposits from a lower-intensity eruptive event on 12 January 2011 were also extensively surveyed (Andronico et al., 2014). A lava fountain from 21:50 to 23:30 UTC reached around 800 m height, with an ash plume estimated at 9 km a.s.l. and lapilli up to 5 cm in diameter collected 5 km from the vent (Andronico et al., 2014; Calvari et al., 2011; Donnadieu et al., 2016). Large-clast deposition from the eruptive plume is also described for many smaller lava fountains, which produced less extensive ash plumes with fallout of large clasts confined to a small area proximal (<5 km) to the vent (for example, Andronico et al., 2009).
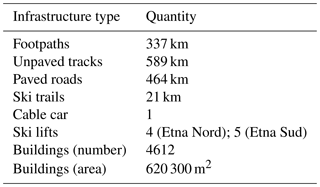
Large-clast sedimentation is likely to be a hazard within 10 km of the summit craters, an area within the Ente Parco dell'Etna Regional Nature Park which has no permanent population. However, the park is very popular with visitors and an estimated 1.3 million people visited the craters in 2010 (Parco dell'Etna, 2013) with the visitor number increasing by 50 % since the park was made a UNESCO world heritage site in 2013 (Perricone, 2017). Infrastructure at risk of impact includes some 1390 km of footpaths, unpaved tracks and paved roads, as well as over 4600 buildings, including commercial and residential properties but no critical facilities such as hospitals or schools (Fig. 1 and Table 1 using data from OpenStreetMap and Ente Parco dell'Etna). In addition, there is a cable car and two ski areas (Etna Nord and Etna Sud) with ski lifts and around 21 km of ski trails (OpenStreetMap Foundation, 2017a, b).
Table 1Infrastructure within 10 km of the summit craters of Mount Etna (OpenStreetMap Foundation, 2017a, from 2017b). The buildings include an observatory and huts, as well as industrial, commercial and residential buildings.
For the purposes of this work, we have considered the most-used buildings and infrastructure around the summit area of Etna (Fig. 1). On the southern slope they are the top station of the Funivia dell'Etna cable car (waiting area for the hundreds to thousands of tourists that visit the volcano summit daily or use the ski slopes in winter) and Baita delle Guide (a transportable shelter located at around 2900 m in the waiting area for tourists using four-wheel drive buses). The Pizzi Deneri Observatory (2847 m a.s.l.; a building used by volcanologists for field schools, research and monitoring activities) and Rifugio Citelli (at the end of a no-through secondary road, used by hundreds of people especially at weekends and during the ski season) are on the northern slope. Furthermore, our study also covers the infrastructure in two main tourist areas, i.e. Etna Sud (at 1920 m) and Etna Nord (at 1810 m), commonly known as Rifugio Sapienza (an area visited by up to thousands of visitors during the day) and Piano Provenzana (a very popular ski station), respectively. Finally, several secondary mountain huts are also located along tracks at mid-slopes, especially on the western and northern slopes of the volcano (Fig. 1).
We make use of the particle sedimentation model of Rossi et al. (2019) in order to simulate the transport of clasts within a volcanic plume and their sedimentation. This model modifies the well-known methodology introduced by Carey and Sparks (1986) in order to take into account the effects of wind on the eruptive column. Particles are first released into the atmosphere from the clast support envelope, a region of the plume where the velocity of the gas mixture equals the terminal velocity of the clast. Clast trajectories are then computed solving the second law of motion in a windy atmosphere. The model applies best to centimetre-scale particles that show a reduced, but not negligible, coupling with the gas mixture of the plume. Plume dynamics are described based on the model of Degruyter and Bonadonna (2012).
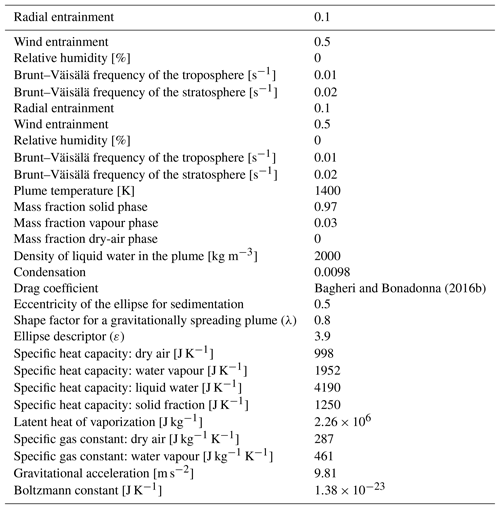
The main inputs to the model are particle parameters, eruption parameters, wind profiles and a digital elevation model (DEM) for the area being considered. The particle parameters include size, density, the Stokes drag coefficient kS (for particles falling in random orientation) and the Newtonian drag coefficient kN (for particles falling in a gas). kS and kN are as described in Bagheri and Bonadonna (2016b). Eruption parameters include the mass eruption rate (MER) and the number of particles to be sedimented (described further in Sect. 3.4.1). Three-dimensional wind profiles are used to define the wind field, which can vary with distance from the vent.
The model takes a three-dimensional wind profile and creates the wind field across the modelled area, and it then uses the input MER to model the maximum height of the plume above the eruptive vent. The clast diameter and the number of particles to be sedimented are fixed for each simulation and particles are released from the vent. When their (downward) terminal velocity exceeds the plume upward velocity they start to fall and the model calculates the trajectory of each particle until it reaches the ground, with the terrain being defined by the DEM. The modelled ground surface is gridded, and the size of the grid cells is equal to the cell size in the DEM (90 m in our case). For each simulation the point of impact of each sedimented particle is recorded on that grid. The model also calculates the kinetic energy of each particle immediately before impact with the ground.
3.1 Deterministic versus probabilistic approach
The plume model described above can be used deterministically (with one three-dimensional wind profile and fixed eruptive parameters) to compare clast sedimentation with field observations for a specific eruptive event. The model can also be used probabilistically in order to compile maps that contour the probability of a clast of a given diameter reaching a certain location. In the probabilistic approach the model is run several times, with one or more of the initial parameters selected randomly from a statistical distribution. At the end of each simulation, a contour is created from the most external points of ground impact and all grid cells inside that contour are assumed to be impact locations for that simulation. When all the simulations are complete, the number of times each grid cell has been impacted is counted and divided by the total number of simulations, to give the probability of impact for each cell in the grid, which can then be mapped.
3.2 Input data
3.2.1 Wind data
Daily wind profiles taken four times a day from the National Oceanographic and Atmospheric Administration (NOAA, 2017) were analysed for the period 1997–2015 using the MATLAB package TephraProb (Biass et al., 2016c). Wind conditions were found to be very similar for 1 year (2013), 10 years (2006–2015) and the full dataset (19 years, from 1997 to 2015) (see Figs. S1 to S6, for full wind analysis). Results are also in agreement with those of Scollo et al. (2013). Little seasonal difference was found for the expected plume heights up to 15 km a.s.l., with prevailing winds towards the northeastern to south-southeastern sector. The 2006–2015 dataset was selected for the probability assessment and, given the limited extent of large-clast fallout (<10 km from the vent), wind profiles are not considered space-dependent in this assessment (i.e. only one wind profile centred on the vent is considered).
3.2.2 Field observations
The 23 November 2013 event was selected to validate and calibrate the plume model for the description of lava-fountain-fed plumes. In fact, this event represents a lava fountain with one of the largest mass eruption rates at Mount Etna (Andronico et al., 2015; Bonaccorso et al., 2014). For samples collected following the event (Russo, 2016), both the median and the average of the five largest clasts (measured using the method of Bagheri and Bonadonna, 2016a) were calculated and the drag coefficients, kS and kN, were derived for use in the hazard analysis, as described in Appendix A. We found that the median is more stable than the average of the five largest clasts at the scale of the outcrop (Tables A1 and A2), as also concluded by Bonadonna et al. (2013); however, isopleth maps compiled based on the median values (and corresponding downwind and crosswind ranges) are not more stable than the isopleth maps compiled based on the average of the five largest clasts (Fig. A1). In addition, modelled contours more closely match values calculated using the average of the five largest clasts (Fig. A2).
3.3 Model validation and calibration
The model was validated and calibrated to the 23 November 2013 lava fountain by varying the modelled MER to produce the observed plume height of 11 km a.s.l. (Corradini et al., 2016), using wind conditions for the time of the eruption. Table B1 summarizes the model input parameters that were fixed for this study and Table B2 lists the input parameters used for the model calibration. During an eruption MER will vary but because reported plume heights are usually the maximum height achieved by the plume and MER is estimated based on plume height (Degruyter and Bonadonna, 2012); the modelled MER represents the maximum MER for the eruptions. Given that a range of MER values could equally produce the observed plume height, the best-fit MER (5.4×106 kg s−1) was found by comparing modelled clast size contours and the field data. Figure A2 shows the modelled contours for this MER, which most closely match the field observations calculated using the average of the five largest clasts method (see Appendix A for use of the five largest clasts in model validation).
3.4 Sensitivity analysis
3.4.1 Number of particles
The optimum number of particles to be released from an eruptive plume was tested using simulations of 100, 500, 1000 and 5000 particles, keeping both the wind and the particle diameter (5 cm) fixed, in order to maximize model performance in terms of machine time. For this analysis we used the three-dimensional wind profile for 12 December 2015 from 14:00 to 16:00 UTC, when wind speeds were high, which results in particle sedimentation over a wide area, making the effect of changing particle numbers easier to identify. Using 100 particles produced an angular contour, indicating particle density within the contour is low and hence the contour is likely to change with each simulation. In contrast, contours for 500 or more particles were smooth and almost completely overlapped (Fig. S7a). As a result, 500 particles were selected as suitable for the hazard analysis as described below.
3.4.2 Particle density
The sensitivity of the model output to particle density was tested using simulations with particle densities selected from end member values measured at Mount Etna. In particular, we considered the events of 12 January 2011 (1000 kg m−3), 23 November 2013 (865 kg m−3) and 3 December 2015 (760 kg m−3) (Andronico et al., 2015, 2014; Russo, 2016). The wind was fixed to 12 December 2015 from 14:00 to 16:00 UTC as for the particle number test. The contour for the lowest-density clasts is 26 % larger than for the highest-density clasts (Fig. S7b), mostly due to the clasts reaching a greater distance from the crater. Therefore, particle density is an important variable for the hazard analysis: the lower the density, the larger the impacted area.
3.4.3 Number of simulations
The stability of the results in terms of the impacted area is dependent on the number of runs used, and to test this different numbers of runs were compiled for a 5 cm clast. More simulations give a more stable result but, as each additional simulation takes time, a balance must be found between confidence in the output and a realistic timescale for the simulations. For very low impact probabilities (<1 %), the hazard area is very sensitive to the number of simulations (as shown in Figs. S8 and S9) because for each additional run, new locations will receive one impact. Areas with probability <1 % were excluded from further analysis because of the high level of uncertainty, and for each simulation the probability contours were treated as stable if the associated area changed by <3 % between different numbers of simulations. Different numbers of simulations are used for the different probabilistic scenarios considered (e.g. Appendix B).
3.4.4 Choice of eruption crater
As mentioned earlier, lava fountains have been produced at different vents on Mount Etna and it is not easy to predict where the next lava fountain will occur. In order to identify the sensitivity of model outputs to the choice of eruptive vent, the 23 November 2013 event was separately modelled as an eruption from each of the five summit vents. Although the hazard zones largely overlap, lava fountains from the Northeast Crater (NEC), Voragine or Bocca Nuova are likely to extend the hazardous area further north compared to events from the Southeast Crater (SEC) and NSEC (Fig. S10). The NSEC was chosen as the primary vent for our hazard assessment, as this vent has produced most of the lava fountains over the past 5 years (Table S1). However, given the prevailing westerly winds, a probability map from the NSEC may underestimate the northern extent of clast fallout from the NEC, Voragine and Bocca Nuova. To investigate how the location of the eruptive vent affects the infrastructure at risk of impact, the exposure analysis was conducted for high MER events from both the NSEC and Voragine (see the Supplement).
To allow a range of eruptive and atmospheric conditions to be investigated, a probabilistic hazard assessment was completed for three scenarios from the NSEC.
-
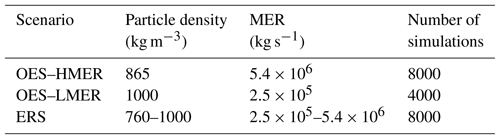
A one eruption scenario (OES) for a high mass eruption rate event (OES–HMER) based on the 23 November 2013 lava fountain (MER = 5.4×106 kg s−1).
-
A OES for a low mass eruption rate event (OES–LMER) based on the 12 January 2011 lava fountain (MER = 2.5×105 kg s−1).
-
An eruption range scenario (ERS) using a Monte Carlo approach where values of particle density and MER were randomly sampled from within a statistical distribution based on previous activity at Mount Etna (MER = kg s−1).
For the OESs, eruptive parameters are fixed but the wind is selected randomly from the available dataset, while for the ERS the eruptive parameters are also randomly selected from an associated probability density function. The OES–HMER event was selected as being the largest MER so far experienced from a lava fountain at Mount Etna and the OES–LMER event was the smallest MER likely to cause significant hazard beyond the immediate proximal area. For the ERS, a uniform distribution was chosen for particle density, but to account for small eruptions occurring more frequently than large ones, a logarithmic distribution of MER was used (Biass et al., 2016b; Bonadonna, 2006). In Appendix C we report the frequency distributions for the sampled particle density and MER, the distribution of sampled wind profiles and the resulting distribution of plume height (calculated from the combination of MER and wind speed) (Fig. C1). These confirm that the sampled values are within the expected frequency distributions and the winds are representative of the 2006–2015 dataset. The low frequency for the smallest MER ( kg s−1) suggests that some plumes with this MER are not buoyant and thus are discarded by the model. The modelled plume heights (Fig. C1c) range from 6.0 to 14.9 km a.s.l.
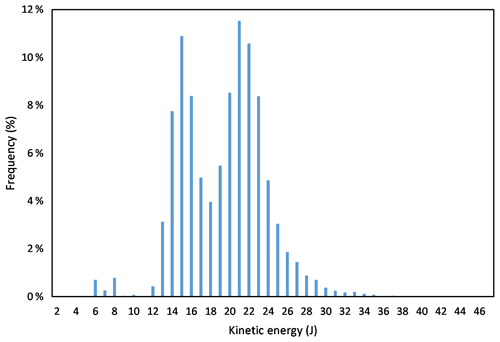
For each scenario a clast diameter of 5 cm was selected as being likely to cause significant injury (Peter Baxter, personal communication, 2017). Hereafter particles >5 cm are defined as hazardous clasts. The damage caused by a particle on impact depends on its kinetic energy and the modelled particles showed a bimodal distribution of kinetic energies, with peaks at 15 and 21 J and a maximum value of 46 J (shown in Fig. 2). Biomechanical experiments have shown that a dynamic load (such as a falling clast) can cause skull fractures at energies of around 28 J (Yoganandan et al., 1995) and 2 % of modelled clasts had energies above this value. A total of 98 % of clasts had impact energies >10 J and hence may cause building damage, as impact energies of 2 J can damage glass windows and energies >10 J can penetrate roof tiles (Jenkins et al., 2014).
Table B3 summarizes the variable input parameters for each scenario, with the fixed parameters listed in Table B1. For each simulation a wind profile was randomly selected from the 14 608 (four times daily for 10 years) available in the 2006–2015 year NOAA dataset (NOAA, 2017) (Appendix C). The hazard zone, defined as the model grid cells with a probability of impact ≥1 %, was classified into five categories and for each scenario a map was produced showing the area where the probability of impact was >40 %, 30 %–40 %, 20 %–30 %, 10 %–20 % and 1 %–10 % (Fig. 3). Areas with probability of impact <1 % were excluded because at very low probabilities the hazard area is very sensitive to the number of simulations (as shown in Figs. S8 and S9). In each scenario the highest probabilities occur east of the vents, with probabilities no higher than 20 % west of the vent, confirming the influence of the prevailing westerly winds. Table 2 shows the area included within each probability category for each scenario. For probabilities ≥1 %, the hazard zone covers a total area of ∼129 km2, extending up to 8 km from the vent for the OES–HMER, and ∼72 km2, extending up to 6.5 km from the vent for the ERS. The hazard zone for the OES–LMER covers ∼5 km2 and is limited to the area immediately proximal to the craters, confirming that for lava fountain events with MER lower than that of the 12 January 2011 event (2.5×105 kg s−1) any hazardous clast fallout is unlikely to pose a risk to people or infrastructure.
Table 2Area within each probability category in the hazard zone (in km2) for the OES–HMER, OES–LMER and ERS. The hazard zone is the area with a probability of impact from 5 cm clast ≥1 %.
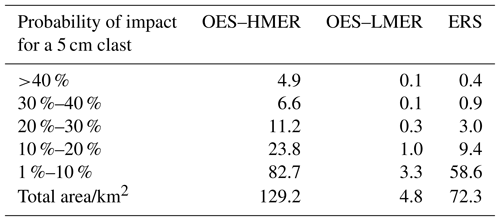
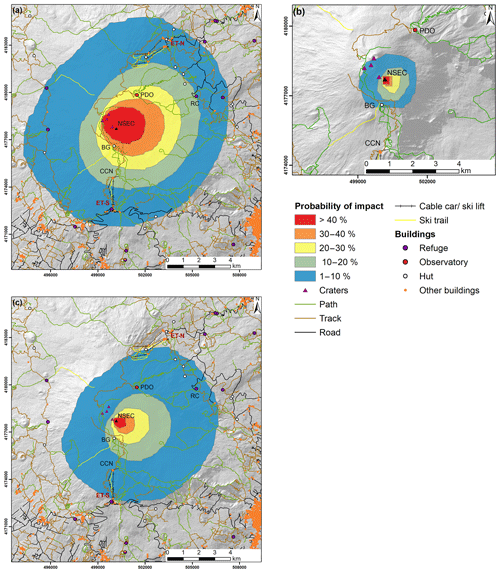
Figure 3Probability map showing exposure of infrastructure to impact from a 5 cm clast for (a) the OES–HMER, (b) the OES–LMER and (c) the ERS. NSEC: New Southeast Crater. Ski areas: ET-N: Etna Nord; ET-S: Etna Sud. BG: Baita delle Guide; CCN: top station of the Funivia dell'Etna cable car; PDO: Pizzi Deneri Observatory; RC: Rifugio Citelli.
The amount of infrastructure at risk was calculated for each scenario. Table 3 summarizes the infrastructure exposed within each hazard zone for each scenario and Fig. 3 shows the infrastructure within the hazard zone for the OES–HMER, the OES–LMER and the ERS (for the NSEC scenario). In order to investigate how this exposure varies for lava fountains from different eruption vents, the probability map for the OES–HMER at the NSEC was translated to be centred on Voragine, which is at the same height as the NSEC and thus we expect particle sedimentation to follow similar trends (Table 3 and Supplement: Fig. S11).
Table 3Infrastructure within the hazard zone for the OES–HMER (from the NSEC and Voragine), OES–LMER (from the NSEC) and ERS (from the NSEC). The hazard zone is the area with a probability of impact from 5 cm clast ≥1 %.
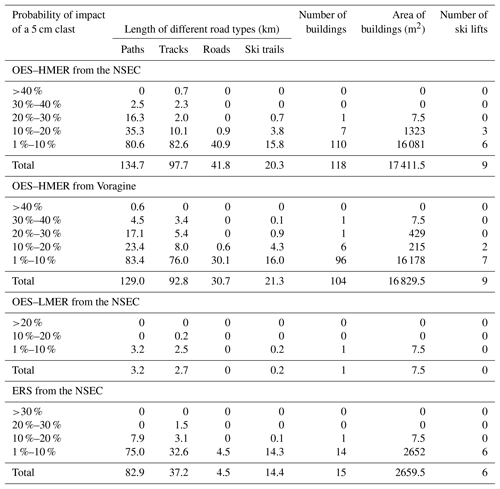
For the OES–HMER from the NSEC, no buildings are in areas with >30 % probability of impact and the only building in the 20 %–30 % area is a hut (Baita delle Guide). The seven buildings in the area with 10 %–20 % probability include Rifugio Citelli, the Pizzi Deneri Observatory and the top station of the Funivia dell'Etna cable car. The Baita delle Guide hut and the observatory are both in a higher hazard category for this scenario from Voragine, although overall fewer roads and buildings are within the total hazard zone (roads: 252.5 km compared to 274.2 km; buildings: 104 compared to 118 for fountains vented from Voragine compared to the NSEC). All the ski lifts are in the hazard zone, with two fully within the 10 %–20 % probability area for the NSEC eruption and only one within the same zone for the Voragine eruption. In both cases one lift crosses the 10 %–20 % and 1 %–10 % areas, as does the Funivia dell'Etna cable car, and the remaining ski lifts are fully in the 1 %–10 % area.
For the OES–LMER scenario, very little infrastructure is at risk, with only 0.2 km roads in the 10 %–20 % probability area and a further 5.7 km plus the Baita delle Guide hut in the 1 %–10 % probability area. For the ERS, no infrastructure is within the area having a probability of impact >30 %. A total of 1.5 km of roads are in the 20 %–30 % probability area, with a further 11 km plus the Baita delle Guide hut in the 10 %–20 % probability area. A total of 112 km of roads, 14 buildings, 14 km of ski trails, 6 ski lifts and the Funivia dell'Etna cable car are in the 1 %–10 % probability area.
The USGS Pedestrian Evacuation Analyst (PEA) tool (Jones et al., 2014) was used to estimate how long it would take for people at the summit to descend to a safe area for each of the hazard scenarios. The main inputs are as follows.
-
A digital elevation model of the area was used (90 m resolution Shuttle Radar Topography Mission (SRTM) data).
-
The hazard area is defined here as the hazard zone described in Sect. 4.
-
The safe zone is defined as the area outside the hazard area.
-
The land cover within the hazard area was used. Each land cover type is assigned a speed conservation value (SCV) which compares the ease of walking on the various surfaces. Values vary from 0 (building) to 1 (road). All roads, paths and tracks were assigned a value of 1 and ski trails were not included as they are likely to be too steep to walk down. Moreover, we assumed that most visitors to the summit area will be within a maximum distance (buffer) from a path or track. The “buffer” was set to 300 m, but to investigate sensitivity to the maximum distance the OES–HMER scenario was also run with a buffer of 500 m. As there is no detailed information on the terrain around each path and track, but it is likely to be slower to walk on than a road, an SCV of 0.65 was assigned.
-
The walking speed, taken as 3.3 km h−1, is defined as a slow walking speed within the PEA tool.
Figure 4 shows evacuation times to reach the safe zone for each scenario, assuming people are a maximum of 300 m from any path. For the OES–HMER, people near to the craters who are furthest from the path will take more than 5 h (313 min) to reach the safe zone. The maximum evacuation time for the OES–LMER is 30 min and for the ERS it is 236 min (about 4 h). Sensitivity to the buffer size is low when increased to 500 m for the OES–HMER, as the maximum time to reach the safe zone increased by only 1 min (Fig. S12).
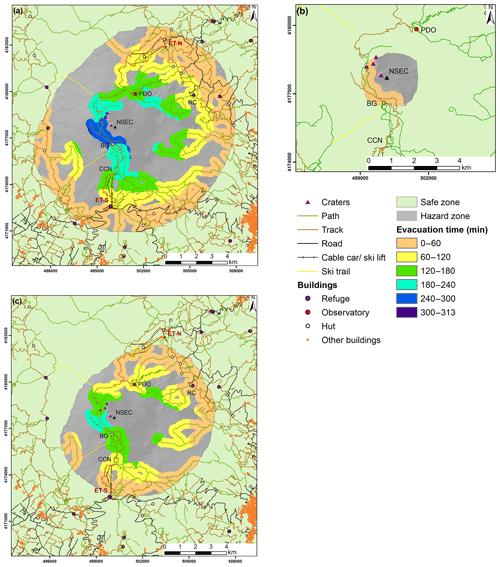
Figure 4Evacuation times to reach the safe zone based on walking speed of 3.3 km h−1, assuming people start a maximum of 300 m from any path for (a) OES–HMER, (b) OES–LMER, (c) ERS. The hazard zone is the area with a probability of impact from 5 cm clast ≥1 %. The safe zone includes areas with a probability of impact <1 %. NSEC: New Southeast Crater. Ski areas: ET-N: Etna Nord; ET-S: Etna Sud. BG: Baita delle Guide; CCN: top station of the Funivia dell'Etna cable car; PDO: Pizzi Deneri Observatory; RC: Rifugio Citelli.
This analysis shows that for large events, people near the summit would, in many cases, be several hours from safety. In addition, given that even relatively minor impact to the skull can cause concussion, escape can be difficult (Baxter and Gresham, 1997). Hence, possible locations for one or two shelters were selected and the analysis was rerun to investigate how that would reduce the time taken to reach a safe location (considering the shelters as additional safe zones). For one shelter, the location was chosen to be within the hazard zone for the OES–LMER, so that it could be used for the whole range of expected events. For two shelters, one was chosen as the top station of the Funivia dell'Etna cable car and the second shelter was located towards the north. Figure 5 shows that, for the ERS, provision of one shelter reduced the maximum evacuation time to 176 min, with only a minor further reduction (18 min) for two shelters. For the OES–HMER, the maximum evacuation time was reduced to just under 4 h (233 min) when one shelter is provided and to 199 min with two shelters (Fig. S13). Increasing the buffer zone around footpaths to 500 m, evacuation times increased to 238 and 207 min, respectively (Fig. S12). For the OES–LMER, adding a shelter did not reduce the maximum evacuation time below 30 min (Fig. S14).
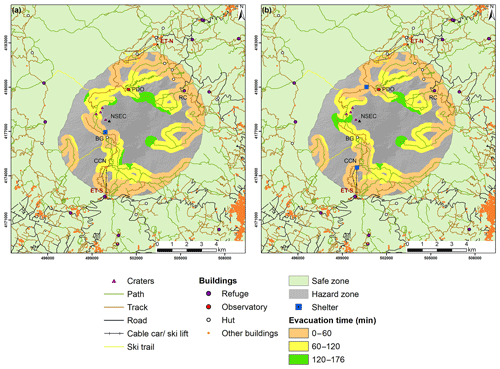
Figure 5Evacuation times to reach the safe zone (for ERS) based on walking speed of 3.3 km h−1, assuming people start a maximum of 300 m from any path, with (a) one shelter and (b) two shelters. The hazard zone is the area with a probability of impact from 5 cm clast ≥1 %. The safe zone includes areas with a probability of impact <1 %. NSEC: New Southeast Crater. Ski areas: ET-N: Etna Nord; ET-S: Etna Sud. BG: Baita delle Guide; CCN: top station of the Funivia dell'Etna cable car; PDO: Pizzi Deneri Observatory; RC: Rifugio Citelli.
7.1 Risk assessment
Large-clast fallout from plumes generated by the frequent lava fountains at Mount Etna poses a substantial risk to people and infrastructure (e.g. Andronico et al., 2015; De Beni et al., 2015). It is therefore important to identify the area likely to be impacted and to understand how long it would take people to evacuate to a safe area. For large eruptions, an area of up to 130 km2 is in the hazard zone; roads have a probability of impact of up to 40 % and the Funivia dell'Etna cable car is also at risk. The area affected depends on the eruptive vent, with lava fountains at Voragine, Bocca Nuova and the NEC resulting in a hazard zone shifted further north and impacting fewer roads and buildings, compared to events from the SEC and NSEC. It is important to bear in mind that even though the majority of lava fountains over the past 5 years have occurred from the NSEC, more than 80 % of the eruptions occurring at Voragine in the past 20 years have been characterized by large plumes (>10 km a.s.l.) (Andronico et al., 2015; Bonaccorso and Calvari, 2017; Calvari and Pinkerton, 2002; Vulpiani et al., 2016; see also Table S1). The probabilistic analysis took account of the range of MER observed in the recent lava fountains at Mount Etna (detailed in Table S1), but it cannot be excluded that a future event could have a higher MER. However, our analysis has identified the smallest MER that could produce hazardous impact from 5 cm clasts (i.e. 2.5×105 kg s−1), as the hazardous clast fallout from lava fountains smaller than the OES–LMER will only affect the area very proximal (≤2 km) to the eruptive vent.
As well as the hazard from large-clast fallout, it is also important to consider impact from ballistic projectiles and hazard from tephra fallout which may all occur simultaneously during an eruption. Probabilistic modelling based on the large explosive eruption at Mount Etna on 5 January 1990 showed that tephra accumulations over 200 kg m−2 occurred up to 10 km from the eruptive vent (Scollo et al., 2013). The area around the Funivia dell'Etna cable car had a 10 %–20 % probability of tephra deposit density ≥100 kg m−2, and this is the same area that had a 1 %–10 % probability of fallout of 5 cm clasts in the current study. Ballistic projectiles ejected from the vent could also pose a hazard on the paths very close to the summit, as happened on the Tongariro Alpine Crossing hiking trail in New Zealand in August 2012 (Fitzgerald et al., 2014). Modelling at La Fossa, Vulcano, Italy, also indicated a range of around 3 km for projectiles with sufficient impact energy to cause injury (Biass et al., 2016a). Large ballistic projectiles have also been observed proximal (<1 km) to the vent at Mount Etna (e.g. Calvari and Pinkerton, 2002).
In order to quantify the exposure of people to hazardous clast fallout, further work is required to characterize visitor numbers and behaviour. For example, tourists are likely to stay near the paths and tracks, while hikers may walk further from the paths. In addition, many scientists visit the summit area, although they are likely to be in contact with colleagues who could warn them of ongoing volcanic activity.
7.2 Emergency management
The PEA tool was run using several assumptions, which require more detailed analysis to confirm the results. The most sensitive assumptions are as follows.
-
Paths and tracks are the fastest routes down from the summit. In most cases this will be true, and people unfamiliar with the area are likely to retrace their steps to descend. However, there may be routes that are faster than using the paths, particularly where slopes are gentle and/or are covered in loose tephra. If these were to be considered as evacuation routes they would, of course, need to be clearly identified to ensure people descending did not get lost. In addition, this study did not consider pedestrian evacuation during the months when the area is covered in snow. During the winter more people may be “off-piste” in areas with no paths, resulting in different evacuation routes compared to the paths used during the summer.
-
The same buffer zone was applied around all paths, tracks and roads and the assumption of a constant buffer zone width can be considered as a worst case. Moreover, the land cover and associated walking speed was assumed to be constant in this zone. In reality, once away from paths the land cover will be variable, and walking speeds could vary considerably between ash, lava and densely vegetated areas.
-
The analysis considered people walking slowly, but as speeds could vary the results have therefore identified maximum times to walk to a safe zone. Moreover, visibility may be limited by ash fallout or sudden changes in weather conditions (e.g. dense fog formation, very frequent at Etna high elevations). Therefore, values need to be assessed empirically.
-
Evacuation from the summit was assumed to be only on foot. However, vehicles may also be available, particularly in the southern sector.
The analysis of evacuation times indicates that, for a large eruption, walking out to a safe area could take several hours, and given that the paroxysmal phase of an eruption often only lasts around an hour (Table S1), provision of short-term emergency shelters near the summit could limit potential casualties. The results for the ERS show that shelters could reduce evacuation times by more than an hour, and further investigation is needed to identify optimal locations. The shelters would have to withstand impact energies of around 46 J, identified as the highest kinetic energy of clasts on impact. Data on likely numbers of visitors at the summit at any time, for example from numbers of people using the cable car, would also be required in order to identify the size of shelters needed. Exercises to evaluate the evacuation routes and times would also be needed. It is important to bear in mind that access to the summit is restricted during orange or red alerts issued by Italian Civil Protection authorities, and hence the expected number of tourists on the summit may be significantly reduced. However, some eruptions (e.g. 23 November 2013) do not give enough warning for the orange or red alert to be issued in time.
The hazard associated with the fallout of large clasts from the convective portion of a volcanic plume has been often overlooked even though field evidence clearly shows that it is a common feature of low- to high-intensity eruptions. As an example, in this study the hazard associated with sedimentation of hazardous (>5 cm) clasts from lava-fountain-fed plumes at Mount Etna was assessed using a new dedicated plume sedimentation model. The model was calibrated using field and wind data for the largest eruption to date of a lava fountain at Mount Etna, and a probabilistic hazard assessment was then carried out using three scenarios. Hazard scenarios were based on events with high and low MER plus one scenario which sampled both a range of eruptive parameters (e.g. MER, particle density) and wind conditions. The area at risk of impact from sedimentation of hazardous clasts (>5 cm in diameter) was mapped for each scenario, the exposed infrastructure was quantified and pedestrian evacuation times from the summit were investigated. From the hazard analysis of the NSEC we can make the following conclusions.
-
For the OES–HMER, the hazard zone (area with probability of impact ≥1 %) covered an area of 129 km2 and extended up to 8 km from the vent. Exposed infrastructure for an eruption from the NSEC included some 274 km of paths and 118 buildings, while for an eruption from Voragine 235 km of paths and 104 buildings were exposed.
-
For the OES–LMER, the hazard zone covered 5 km2 and extended up to 1.4 km from the vent. Exposed infrastructure included 6 km of paths and only one building (a mountain hut).
-
For the ERS, the hazard zone covered 72 km2 and extended up to 6.5 km from the vent. Exposed infrastructure included some 125 km of paths and 15 buildings, including mountain huts, an observatory and Rifugio Citelli.
-
The maximum evacuation time for people walking down from the summit was just under 5 h for the OES–HMER, almost 4 h for the ERS and 30 min for the OES–LMER.
-
For large eruptions, provision of one or two shelters could reduce maximum evacuation times by up to 2 h.
-
The impact of an eruption from Voragine, Bocca Nuova or the NEC is of similar magnitude but with the affected area slightly shifted to the north (Table 3 and Fig. S11). Future work is needed to confirm how land cover (and hence likely walking speed) varies across the area and to understand how evacuation routes change in winter, when paths may be covered in snow. The proposed approach could also help in locating the shelters; their structure and capacity should be decided by the Italian Civil Protection authorities, based on information provided by the private companies that manage tourist excursions to the summit, i.e. ski lifts, four-wheel drive vehicles and hiking. A communication strategy would also be important to ensure that shelters do not encourage reckless behaviour, with people feeling safer about going into the hazard zone when the paroxysmal phase of an eruption has started. The model has already been implemented within the operational platform of Istituto Nazionale di Geofisica e Vulcanologia, Osservatorio Etneo (INGV-OE) for rapid daily hazard assessment for Italian Civil Protection use. The proposed methodology can be easily applied to other volcanoes and results obtained for Mount Etna show how the assessment of the hazard associated with hazardous clasts (>5 cm) from eruptive plumes should be accurately characterized, particularly for volcanoes that are a popular destination for tourists and where visitors can reach the summit areas.
Most of the data are made available in main tables and the Supplement. Additional data are available upon request, based on a collaborative agreement.
A detailed field survey was carried out by Russo (2016), who measured the three axes of 10 to 15 clasts in three different areas, each of 25 m2, at 16 locations at different distances from the vent. The equivalent diameter of each clast, deq, was calculated using the following equation (Bagheri and Bonadonna, 2016a):
where L, I and S are the three axes of the clasts (large, intermediate and small). Both the median and the average of the largest five clasts were derived for each of the three areas and for the three areas together in each of the 16 locations. Shape descriptors FS and FN were also calculated:
where flatness, and elongation, (Bagheri et al., 2015). The Stokes drag coefficient, kS (for particles falling in random orientation), and the Newtonian drag coefficient, kN (for particles falling in a gas), were then calculated for use in the hazard analysis (Bagheri and Bonadonna, 2016b):
Table A1Variance across the three areas of 10 to 15 clasts for each outcrop and across the whole deposit for locations from Fig. A2. Deposit variance indicates the average of the outcrop variance.
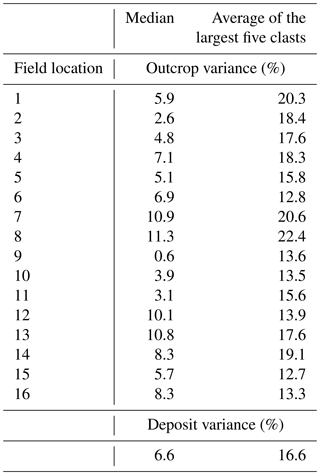
At individual field locations, median values were found to be more stable than values using the average of the largest five clasts, confirming the results of Bonadonna et al. (2013) (Table A1); however, over the whole sampling area both methods produced widely varying values of crosswind and downwind ranges (Fig. A1 and Table A2) indicating that the use of the median values does not improve the stability of isopleth maps at the scale of the deposit. In addition, Fig. A2 shows that modelled contours contain the median values but more closely match the values calculated using the average of the five largest clasts. Based on this analysis, we conclude that the use of the average of the five largest clasts for the comparison of field data with clast sedimentation modelling (e.g. Burden et al., 2011; Carey and Sparks, 1986; Rossi et al., 2019) is the most appropriate and induces a variability at the level of the deposit (i.e. isopleth map) similar to that induced by the median values (even though median values are more stable at the level of the outcrop).
Table A2Percentage discrepancy amongst downwind and crosswind distances of individual contours (as defined by Carey and Sparks, 1986) for the isopleth maps of Fig. A1. All: median or average of five clast values calculated considering all clasts from the three areas of individual outcrops (30–45 clasts). Largest: largest median or average of five clast values of the three areas (with 10–15 clasts within each area). Smallest: smallest median or average of five clast values of the three areas (with 10–15 clasts within each area).
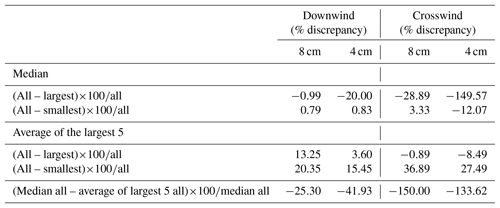
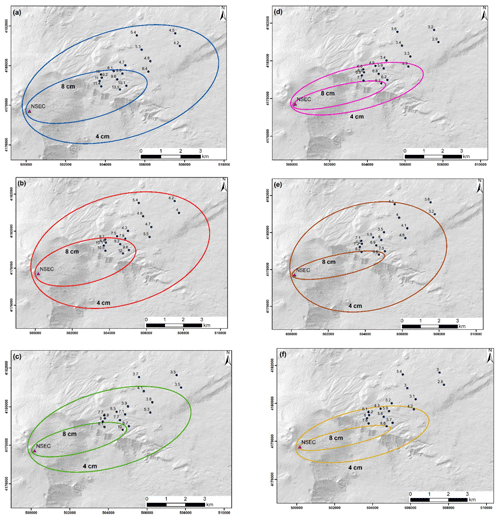
Figure A1Isopleth maps showing the contours of 4 and 8 cm clasts using different averaging strategies of field data. Note that values indicate average (a, b, c) and median (d, e, f). (a) Average of the five largest clasts, combining all three sampling areas at each location. (b) The largest value of the average of the five largest clasts out of the three sampling areas of each location. (c) The smallest value of the average of the five largest clasts out of the three sampling areas of each location. (d) The median value of the combination of all three sampling areas at each location. (e) The largest value of the median of the combination of the three sampling areas of each location. (f) The smallest value of the median of the combination of the three sampling areas of each location.
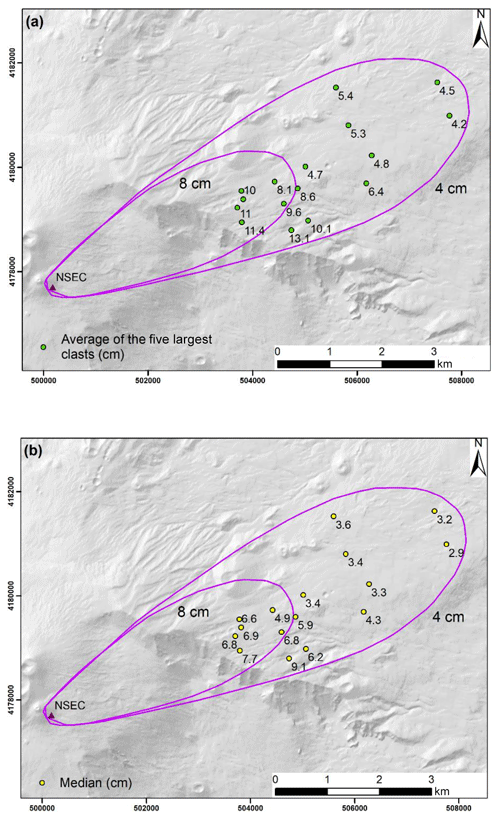
Figure A2Comparison of modelled contours for 4 and 8 cm (compiled using the model of Rossi et al., 2019) and field data values calculated using (a) the average of the five largest clasts (considering all three sampling areas at each location) and (b) the median values (considering all three sampling areas at each location). Note that to facilitate the comparison, model contours are the same in both figures, while observation data are different, i.e. average of five largest clasts and median values, respectively.
Table B2Input parameters used to calibrate the model. NSEC: New Southeast Crater. Particle density, kS and kN are median values calculated from field data.
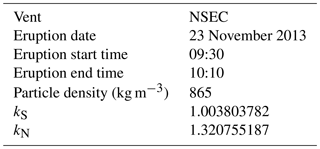
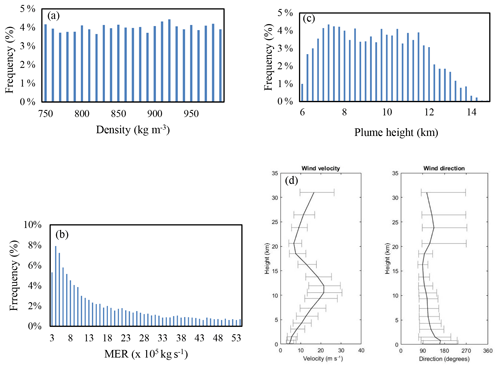
Figure C1Parameters sampled for the ERS. (a) Particle density, (b) mass eruption rate, (c) plume height, (d) wind speed and direction (created in TephraProb) (Biass et al., 2016c; NOAA, 2017). Plume height depends on mass eruption rate and wind speed. Wind direction is the direction towards which the wind blows, which is indicated in degrees from north.
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-19-589-2019-supplement.
SO carried out all the analysis and prepared the manuscript. ER adapted the plume model of Rossi et al. (2019) to this case study and assisted SO in result analysis. CB designed the project in collaboration with INGV-OE and RC and assisted SO and ER in the application of the plume model and probabilistic analysis to the case study. CF assisted SO for the use of GIS and application of the USGS Pedestrian Evacuation Analyst tool as well as for the analysis of potential impact. DA, RC and SS provided field observations and assisted in the application to the case study. All authors participated in the interpretation of results and finalization of the manuscript.
The authors declare that they have no conflict of interest.
The authors are grateful to Mauro Rosi and Peter Baxter for discussion of
the potential impact of large clasts from volcanic plumes. Wim Degruyter is
thanked for discussion about plume modelling, while Sebastien Biass is thanked
for assistance in the wind analysis. The authors are grateful to Salvo
Spina from Ente Parco dell'Etna for providing the data on buildings and
paths. The work formed part of an MSc project (SO). Thanks to project
supervisor Malcolm Whitworth and to the University of Geneva Swiss European
Mobility Program. The work was supported in the framework of the
Dipartimento della Protezione Civile–Istituto Nazionale di Geofisica e
Vulcanologia Agreement 2012–2021 and by the Swiss National Science Foundation
(no. 200021_163152). The contents of this paper represent the
authors' ideas and do not necessarily correspond to the official opinion and
policies of the Italian Department of Civil Protection.
Edited by: Giovanni Macedonio
Reviewed by: three anonymous referees
Andronico, D., Cristaldi, A., and Scollo, S.: The 4–5 September 2007 lava fountain at South-East Crater of Mt Etna, Italy, J. Volcanol. Geotherm. Res., 173, 325–328, https://doi.org/10.1016/j.jvolgeores.2008.02.004, 2008.
Andronico, D., Scollo, S., Cristaldi, A., and Ferrari, F.: Monitoring ash emission episodes at Mt. Etna: The 16 November 2006 case study, J. Volcanol. Geotherm. Res., 180, 123–134, https://doi.org/10.1016/j.jvolgeores.2008.10.019, 2009.
Andronico, D., Scollo, S., Cristaldi, A., and Lo Castro, M. D.: Representivity of incompletely sampled fall deposits in estimating eruption source parameters: a test using the 12–13 January 2011 lava fountain deposit from Mt. Etna volcano, Italy, Bull. Volcanol., 76, 861, https://doi.org/10.1007/s00445-014-0861-3, 2014.
Andronico, D., Scollo, S., and Cristaldi, A.: Unexpected hazards from tephra fallouts at Mt Etna: the 23 November 2013 lava fountain, J. Volcanol. Geotherm. Res., 304, 118–125, https://doi.org/10.1016/j.jvolgeores.2015.08.007, 2015.
Bagheri, G. and Bonadonna, C.: Aerodynamics of volcanic particles: characterization of size, shape, and settling velocity, in: Volcanic ash: hazard observation, edited by: Mackie, S., Cashman, K., Ricketts, H., Rust, A., and Watson, M., 39–52, Elsevier, London, 2016a.
Bagheri, G. and Bonadonna, C.: On the drag of freely falling non-spherical particles, Powder Technol., 301, 526–544, https://doi.org/10.1016/j.powtec.2016.06.015, 2016b.
Bagheri, G., Bonadonna, C., Manzella, I., and Vonlanthen, P.: On the characterization of size and shape of irregular particles, Powder Technol., 270, 141–153, https://doi.org/10.1016/j.powtec.2014.10.015, 2015.
Barsotti, S., Neri, A., Bertagnini, A., Cioni, R., Mulas, M., and Mundula, F.: Dynamics and tephra dispersal of Violent Strombolian eruptions at Vesuvius: insights from field data, wind reconstruction and numerical simulation of the 1906 event, Bull. Volcanol., 77, 58, https://doi.org/10.1007/s00445-015-0939-6, 2015.
Baxter, P. J. and Gresham, A.: Deaths and injuries in the eruption of Galeras Volcano, Colombia, 14 January 1993, J. Volcanol. Geotherm. Res., 77, 325–338, https://doi.org/10.1016/S0377-0273(96)00103-5, 1997.
Bertin, D.: 3-D ballistic transport of ellipsoidal volcanic projectiles considering horizontal wind field and variable shape-dependent drag coefficients, J. Geophys. Res.-Solid Earth, 122, 1126–1151, https://doi.org/10.1002/2016JB013320, 2017.
Biass, S., Scaini, C., Bonadonna, C., Folch, A., Smith, K., and Höskuldsson, A.: A multi-scale risk assessment for tephra fallout and airborne concentration from multiple Icelandic volcanoes – Part 1: Hazard assessment, Nat. Hazards Earth Syst. Sci., 14, 2265–2287, https://doi.org/10.5194/nhess-14-2265-2014, 2014.
Biass, S., Falcone, J.-L., Bonadonna, C., Di Traglia, F., Pistolesi, M., Rosi, M., and Lestuzzi, P.: Great Balls of Fire: A probabilistic approach to quantify the hazard related to ballistics – a case study at La Fossa volcano, Vulcano Island, Italy, J. Volcanol. Geotherm. Res., 325, 1–14, https://doi.org/10.1016/j.jvolgeores.2016.06.006, 2016a.
Biass, S., Bonadonna, C., di Traglia, F., Pistolesi, M., Rosi, M., and Lestuzzi, P.: Probabilistic evaluation of the physical impact of future tephra fallout events for the Island of Vulcano, Italy, Bull. Volcanol., 78, 37, https://doi.org/10.1007/s00445-016-1028-1, 2016b.
Biass, S., Bonadonna, C., Connor, L. J., and Connor, C. B.: TephraProb: a Matlab package for probabilistic hazard assessments of tephra fallout, J. Appl. Volcanol., 5, 10, https://doi.org/10.1186/s13617-016-0050-5, 2016c.
Bonaccorso, A. and Calvari, S.: A new approach to investigate an eruptive paroxysmal sequence using camera and strainmeter networks: lessons from the 3–5 December 2015 activity at Etna volcano, Earth Planet. Sc. Lett., 475, 231–241, https://doi.org/10.1016/J.EPSL.2017.07.020, 2017.
Bonaccorso, A., Calvari, S., Linde, A., and Sacks, S.: Eruptive processes leading to the most explosive lava fountain at Etna volcano: the 23 November 2013 episode, Geophys. Res. Lett., 41, 4912–4919, https://doi.org/10.1002/2014GL060623, 2014.
Bonadonna, C.: Probabilistic modelling of tephra dispersion, in: Statistics in volcanology, edited by: Mader, H. M., Coles, S. G., Connor, C. B., and Connor, L. J., 243–259, Geological Society, London, 2006.
Bonadonna, C., Cioni, R., Pistolesi, M., Connor, C., Scollo, S., Pioli, L., and Rosi, M.: Determination of the largest clast sizes of tephra deposits for the characterization of explosive eruptions: a study of the IAVCEI commission on tephra hazard modelling, Bull. Volcanol., 75, 680, https://doi.org/10.1007/s00445-012-0680-3, 2013.
Burden, R. E., Phillips, J. C., and Hincks, T. K.: Estimating volcanic plume heights from depositional clast size, J. Geophys. Res.-Solid Earth, 116, B11206, https://doi.org/10.1029/2011JB008548, 2011.
Bursik, M. I., Sparks, R. S. J., Gilbert, J. S., and Carey, S. N.: Sedimentation of tephra by volcanic plumes: I. Theory and its comparison with a study of the Fogo A plinian deposit, Sao Miguel (Azores), Bull. Volcanol., 54, 329–344, https://doi.org/10.1007/BF00301486, 1992.
Calvari, S. and Pinkerton, H.: Instabilities in the summit region of Mount Etna during the 1999 eruption, Bull. Volcanol., 63, 526–535, https://doi.org/10.1007/s004450100171, 2002.
Calvari, S., Salerno, G. G., Spampinato, L., Gouhier, M., La Spina, A., Pecora, E., Harris, A. J. L., Labazuy, P., Biale, E., and Boschi, E.: An unloading foam model to constrain Etna's 11–13 January 2011 lava fountaining episode, J. Geophys. Res.-Solid Earth, 116, B11207, https://doi.org/10.1029/2011JB008407, 2011.
Carey, S. and Sparks, R. S. J.: Quantitative models of the fallout and dispersal of tephra from volcanic eruption columns, Bull. Volcanol., 48, 109–125, https://doi.org/10.1007/BF01046546, 1986.
Cioni, R., Marianelli, P., and Sbrana, A.: Dynamics of the AD 79 eruption: stratigraphic, sedimentological and geochemical data on the successions from the Somma-Vesuvius southern and eastern sectors, Acta Vulcanol., 2, 109–123, 1992.
Corradini, S., Montopoli, M., Guerrieri, L., Ricci, M., Scollo, S., Merucci, L., Marzano, F., Pugnaghi, S., Prestifilippo, M., Ventress, L., Grainger, R., Carboni, E., Vulpiani, G., and Coltelli, M.: A multi-sensor approach for volcanic ash cloud retrieval and eruption characterization: the 23 November 2013 Etna lava fountain, Remote Sens., 8, 8, https://doi.org/10.3390/rs8010058, 2016.
Corsaro, R. A., Andronico, D., Behncke, B., Branca, S., Caltabiano, T., Ciancitto, F., Cristaldi, A., De Beni, E., La Spina, A., Lodato, L., Miraglia, L., Neri, M., Salerno, G., Scollo, S., and Spata, G.: Monitoring the December 2015 summit eruptions of Mt. Etna (Italy): Implications on eruptive dynamics, J. Volcanol. Geotherm. Res., 341, 53–69, https://doi.org/10.1016/j.jvolgeores.2017.04.018, 2017.
Costa, A., Dell'Erba, F., Di Vito, M. A., Isaia, R., Macedonio, G., Orsi, G., and Pfeiffer, T.: Tephra fallout hazard assessment at the Campi Flegrei caldera (Italy), Bull. Volcanol., 71, 259–273, https://doi.org/10.1007/s00445-008-0220-3, 2009.
De Beni, E., Behncke, B., Branca, S., Nicolosi, I., Carluccio, R., D'Ajello Caracciolo, F., and Chiappini, M.: The continuing story of Etna's New Southeast Crater (2012–2014): evolution and volume calculations based on field surveys and aerophotogrammetry, J. Volcanol. Geotherm. Res., 303, 175–186, https://doi.org/10.1016/j.jvolgeores.2015.07.021, 2015.
Degruyter, W. and Bonadonna, C.: Improving on mass flow rate estimates of volcanic eruptions, Geophys. Res. Lett., 39, L16308, https://doi.org/10.1029/2012GL052566, 2012.
Donnadieu, F., Freville, P., Hervier, C., Coltelli, M., Scollo, S., Prestifilippo, M., Valade, S., Rivet, S., and Cacault, P.: Near-source Doppler radar monitoring of tephra plumes at Etna, J. Volcanol. Geotherm. Res., 312, 26–39, https://doi.org/10.1016/j.jvolgeores.2016.01.009, 2016.
Fitzgerald, R. H., Tsunematsu, K., Kennedy, B. M., Breard, E. C. P., Lube, G., Wilson, T. M., Jolly, A. D., Pawson, J., Rosenberg, M. D., and Cronin, S. J.: The application of a calibrated 3D ballistic trajectory model to ballistic hazard assessments at Upper Te Maari, Tongariro, J. Volcanol. Geotherm. Res., 286, 248–262, https://doi.org/10.1016/j.jvolgeores.2014.04.006, 2014.
Horwell, C. J. and Baxter, P. J.: The respiratory health hazards of volcanic ash: a review for volcanic risk mitigation, Bull. Volcanol., 69, 1–24, https://doi.org/10.1007/s00445-006-0052-y, 2006.
Jenkins, S. F., Spence, R. J. S., Fonseca, J. F. B. D., Solidum, R. U., and Wilson, T. M.: Volcanic risk assessment: quantifying physical vulnerability in the built environment, J. Volcanol. Geotherm. Res., 276, 105–120, https://doi.org/10.1016/j.jvolgeores.2014.03.002, 2014.
Jenkins, S. F., Wilson, T., Magill, C., Miller, V., Stewart, C., Blong, R., Marzocchi, W., Boulton, M., Bonadonna, C., and Costa, A.: Volcanic ash fall hazard and risk, in: Global volcanic hazards and risk, edited by: Loughlin, S. C., Sparks, R. S. J., Brown, S. K., Jenkins, S. F., and Vye-Brown, C., Cambridge University Press, Cambridge, 2015.
Jones, J. M., Ng, P., and Wood, N. J.: The Pedestrian Evacuation Analyst – geographic information systems software for modeling hazard evacuation potential, available at: https://pubs.usgs.gov/tm/11/c09/ (last access: 8 March 2019), 2014.
NOAA: NCEP reanalysis data, available at: https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.pressure.html (last access: 8 March 2019), 2017.
OpenStreetMap Foundation: OpenSnowMap shapefiles [geospatial data], aAvailable at: http://www.opensnowmap.org/ (last access: 8 March 2019), 2017a.
OpenStreetMap Foundation: OpenStreetMap shapefiles [geospatial data], available at: http://download.geofabrik.de/europe.html (last access: 8 March 2019), 2017b.
Parco dell'Etna: Nomination of Mount Etna for inscription in the World Natural Heritage List UNESCO, available at: http://whc.unesco.org/uploads/nominations/1427.pdf (last access: 8 March 2019), 2013.
Perricone, G.: “Mount Etna”: dopo il riconoscimento Unesco del 2013, cinquanta per cento di turisti in più, available at: http://ilvulcanico.it/mount-etna-dopo-il-riconoscimento-unesco-del-2013-cinquanta-per-cento-di-turisti-in-piu/ (last access: 8 March 2019), 2017.
Rosi, M., Principe, C., and Vecci, R.: The 1631 Vesuvius eruption: a reconstruction based on historical and stratigraphical data, J. Volcanol. Geotherm. Res., 58, 151–182, https://doi.org/10.1016/0377-0273(93)90106-2, 1993.
Rossi, E., Bonadonna, C., and Degruyter, W.: A new strategy for the estimation of plume height from clast dispersal in various atmospheric and eruptive conditions, Earth Planet. Sc. Lett., 505, 1–12, https://doi.org/10.1016/j.epsl.2018.10.007, 2019.
Russo, A.: I prodotti dell'eruzione dell'Etna del 23 novembre 2013, M.S. dissertation, Università degli Studi di Firenze, Florence, Italy, 247 pp., 2016.
Scollo, S., Coltelli, M., Bonadonna, C., and Del Carlo, P.: Tephra hazard assessment at Mt. Etna (Italy), Nat. Hazards Earth Syst. Sci., 13, 3221–3233, https://doi.org/10.5194/nhess-13-3221-2013, 2013.
Sulpizio, R., Mele, D., Dellino, P., and Volpe, L. La: A complex, Subplinian-type eruption from low-viscosity, phonolitic to tephri-phonolitic magma: the AD 472 (Pollena) eruption of Somma-Vesuvius, Italy, Bull. Volcanol., 67, 743–767, https://doi.org/10.1007/s00445-005-0414-x, 2005.
Tsunematsu, K., Chopard, B., Falcone, J.-L., and Bonadonna, C.: A numerical model of ballistic transport with collisions in a volcanic setting, Comput. Geosci., 63, 62–69, https://doi.org/10.1016/j.cageo.2013.10.016, 2014.
Vulpiani, G., Ripepe, M., and Valade, S.: Mass discharge rate retrieval combining weather radar and thermal camera observations, J. Geophys. Res.-Solid Earth, 121, 5679–5695, https://doi.org/10.1002/2016JB013191, 2016.
Wardman, J., Sword-Daniels, V., Stewart, C., and Wilson, T.: Impact assessment of the May 2010 eruption of Pacaya volcano, Guatemala, GNS Science, Lower Hutt, N.Z., Report 2012/09, 90 pp., 2012.
Yoganandan, N., Pintar, F. A., Sances, A., Walsh, P. R., Ewing, C. L., Thomas, D. J., and Snyder, Ri. G.: Biomechanics of skull fracture, J. Neurotrauma, 12, 659–668, https://doi.org/10.1089/neu.1995.12.659, 1995.
Zuccaro, G., De Gregorio, D., and Baxter, P.: Human and structural vulnerability to volcanic processes, in: Volcanic hazards, risks and disasters, edited by: Papale, P. and Shroder, J. F., Elsevier, 2015.
- Abstract
- Introduction
- Proximal exposure at Mount Etna
- Plume modelling
- Hazard assessment
- Exposure analysis
- Pedestrian evacuation analysis
- Discussion
- Conclusions
- Data availability
- Appendix A: Field survey analysis: median versus the average of the five largest clasts
- Appendix B: Model parameters
- Appendix C: Eruption and atmospheric parameters sampled for the eruption range scenario (ERS)
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Proximal exposure at Mount Etna
- Plume modelling
- Hazard assessment
- Exposure analysis
- Pedestrian evacuation analysis
- Discussion
- Conclusions
- Data availability
- Appendix A: Field survey analysis: median versus the average of the five largest clasts
- Appendix B: Model parameters
- Appendix C: Eruption and atmospheric parameters sampled for the eruption range scenario (ERS)
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement