the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Dangerous degree forecast of soil loss on highway slopes in mountainous areas of the Yunnan–Guizhou Plateau (China) using the Revised Universal Soil Loss Equation
Yue Li
Shi Qi
Bin Liang
Junming Ma
Baihan Cheng
Cong Ma
Yidan Qiu
Qinyan Chen
Many high and steep slopes are comprised of special topographic and geomorphic types and formed through mining activities during the construction of mountain expressways. Severe soil erosion may also occur under heavy rainfall conditions. Therefore, predicting soil loss on highway slopes is important in protecting infrastructure and human life. In this study, we investigate Xinhe Expressway located at the southern edge of the Yunnan–Guizhou Plateau. The Revised Universal Soil Loss Equation (RUSLE) is used as the prediction model for soil and water loss on slopes. Geographic information systems, remote sensing technology, field surveys, run-off plot observation testing, cluster analysis and co-kriging calculations are also utilised. The partition of the prediction units of soil loss on the expressway slope in the mountainous area and the spatial distribution of rainfall on a linear highway are studied. Given the particularity of the expressway slope in the mountainous area, the model parameter is modified, and the risk of soil loss along the mountain expressway is simulated and predicted under 20- and 1-year rainfall return periods. The following results are obtained. (1) Natural watersheds can be considered for the prediction of slope soil erosion to represent the actual situation of soil loss on each slope. Then, the spatial location of the soil erosion unit can be determined. (2) Analysis of actual observation data shows that the overall average absolute error of the monitoring area is 0.39 t ha−1, the overall average relative error is 33.96 % and the overall root mean square error is between 0.21 and 0.66, all of which are within acceptable limits. The Nash efficiency coefficient is 0.67, indicating that the prediction accuracy of the model satisfies the requirements. (3) Under the 1-year rainfall return period condition, we find through risk classification that the percentage of prediction units with no risk of erosion is 78 %. The soil erosion risk is low and does not affect road traffic safety. Under the 20-year return period rainfall condition, the percentage of units with high and extremely high risks is 7.11 %. The prediction results can help adjust the design of water and soil conservation measures for these units.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(15850 KB)
- Corrigendum
-
Supplement
(170 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(15850 KB) - Corrigendum
-
Supplement
(170 KB) - BibTeX
- EndNote
China has gradually accelerated its construction of highways in recent years, improved its transportation networks and promoted rapid economic development (Jia et al., 2005; Dong and Zeng, 2003). With the implementation of the Western Development Strategy, advanced requirements for the construction of expressways have been proposed to connect coastal plains and inland mountains. However, many unstable high and steep slopes, such as natural, excavation and fill slopes, are inevitably formed by the frequent filling and deep digging along expressways in mountain areas.
The slope is the most fragile part of an expressway in a mountain area. During rainy seasons, soil erosion is easily caused by rainwash and leads to considerable damage (Fig. 1). At present, China's highway industry remains in a period of rapid development. At the end of 2017, the total length of road exceeded 4 773 500 km, whilst that of highways was 136 500 km (Ren, 2018; Mori et al., 2017; Kateb et al., 2013; Zhou et al., 2016). Statistics further indicate that in the next 20–30 years, the expressways in China will have a total length of more than 40 000 km. For every kilometre of highway, the corresponding bare slope area is expected to reach 50 000–70 000 m2 (Wang, 2006). The annual amount of soil erosion is 9000 g m−3, which can cause 450 t of soil loss annually (Y. J. Chen et al., 2010). The soil loss of roadbed slopes differs from the soil loss in woodlands and farmlands. Forestlands and farmlands are generally formed after years of evolution and belong to the native landscape. Most of the slopes of these land types are gentle and stable (Kateb et al., 2013). Moreover, traditional soil and water conservation research has focused on slopes with a grade of 20 % or below, but roadbed slopes of highways generally have a grade of 30 % or above (Zhou, 2010). Soil erosion on roadbed side slopes affects not only soil loss along highways but also road operation safety (Gong and Yang, 2016; Jiang et al., 2017). Therefore, soil erosion on the side slopes of mountain expressways must be studied to control soil erosion, improve the ecological environment of expressways and realise sustainable land utilisation (Wang et al., 2005; Yang and Wang, 2006).
The Revised Universal Soil Loss Equation (RUSLE) is a set of mathematical equations used to estimate the average annual soil loss and sediment yield resulting from inter-rill and rill erosion (Renard et al., 1997; Foster et al., 1999; Zerihun et al., 2018; Toy et al., 2002). RUSLE was derived from the theory of erosion processes and has been applied to more than 10 000 plot years of data from natural rainfall plots and numerous rainfall simulation plots. RUSLE is an exceptionally well-validated and well-documented equation. It was conceptualised by a group of nationally recognised scientists and soil conservationists with extensive experience in erosion processes (Soil and Water Conservation Society, 1993).
The use of RUSLE models as predictive tools for the quantitative estimation of soil erosion has developed (Panagos et al., 2018; Cunha et al., 2017; Taye et al., 2017; Renard, 1997; Bosco et al., 2015; Cai et al., 2000; Millward and Mersey, 1999). The range of application of these models involves nearly every aspect of soil erosion. Moreover, many scientists have conducted useful explorations to modify the model's parametric values and improve its simulation accuracy.
Tresch et al. (1995), in a study in Switzerland, argued that slope length (L) and slope steepness (S) are crucial factors in soil erosion prediction, and these parameters significantly influence the erosion values calculated by RUSLE. All existing S factors can be derived only from gentle slope inclinations of up to 32 %; however, many cultivated areas are steeper than this critical value. A previous study used 18 plot measurements on transects along slopes with steepness from 20 % to 90 % to qualitatively assess the most suitable S factors for steep subalpine slopes; the results showed that the first selection of the S factor is possible for slopes beyond the critical steepness of 25 % (Tresch et al., 1995). Rick et al. (2001) found that using the Universal Soil Loss Equation (USLE) and RUSLE soil erosion models at regional landscape scales is limited by the difficulty of obtaining an LS factor grid suitable for geographic information system (GIS) applications. Therefore, their modifications were applied to the previous ARC Macro Language (AML) code to produce a RUSLE-based version of the LS factor grid. These alterations included replacing the USLE algorithms with their RUSLE counterparts and redefining the assumptions on slope characteristics. In areas of the western USA where the models were tested, the RUSLE-based AML program produced LS values that were roughly comparable to those listed in the RUSLE handbook guidelines (Rick et al., 2001). Silburn (2011) showed that estimating the soil erodibility factor (K) from soil properties (derived from cultivated soils) provides a reasonable estimate of K for the main duplex soils at the study site, as long as the correction for undisturbed soil is used to derive K from the measured data before application to the USLE model (Silburn, 2011). Wu (2014) adopted GIS and RUSLE methods to analyse the risk pattern of soil erosion in the affected road zone of Hangjinqu Highway in Zhuji, Zhejiang Province. Digital elevation model (DEM) data, rainfall records, soil type data, remote sensing imaging and a road map of Hangjinqu Highway were used for GIS and RUSLE analyses (Wu et al., 2014). Z. W. Chen et al. (2010), who initially considered the terrain characteristics of roadbed side slopes and conducted a concrete analysis of the terrain factor calculation method in RUSLE, evaluated a compatible terrain factor computational method of roadbed side slopes and proposed a revised method based on the measured data of soil erosion on the subgrade side slope of Hurongxi Expressway (from Enshi to Lichuan) in Hubei Province. The results indicated that (1) the slope length factor in RUSLE can be calculated by , but m should not be computed using the original method for highway subgrade side slope because its gradient surpasses the generally applicable scope of RUSLE. Moreover, (2) the slope length factor (L) of the highway subgrade side slope can be calculated by (Z. W. Chen et al., 2010). Zhang (2016) investigated the spatio-temporal distribution of soil erosion on a ring expressway before and after construction using a land use/cover map of Ningbo in 2010. The topographic map of the North Ring Expressway and field survey data were collected for the DEM. Rainfall data were also collected from local hydrological stations. On the basis of the collected data, the spatial distribution of the factors in the RUSLE model was calculated, and soil erosion maps of the North Ring Expressway were estimated. Then, the soil erosion amount was calculated at three different stages by RUSLE. The results showed that slight erosion was dominant during the preconstruction and natural recovery periods, which accounted for 98.53 % and 99.73 %, respectively. During the construction period, mild erosion and slight erosion had the largest values and accounted for 52.5 % and 35.4 %, respectively. Soil erosion during the construction period was mainly distributed in temporary ground soil (Zhang et al., 2016).
However, the common methods used to fit the parameters can affect the findings, and minimising the sum of the squares of errors for soil loss may provide better results than simply fitting an exponential equation. Yang (2014) found that the C factor, as a function of fractional bare soil and ground cover, can be derived from MODIS data at regional or catchment scales. The method offered a meaningful estimate of the C factor for determining ground cover impact on soil loss and erosion hazard areas. The method performed better than commonly used techniques based on green vegetation only (e.g. normalised difference vegetation index, NDVI), and it was appropriate for estimating the vegetation cover management factor (C) in the modelled hillslope erosion in New South Wales, Australia, using emerging fractional vegetation cover products. Moreover, the approach effectively mapped the spatio-temporal distribution of the RUSLE cover factor and the hillslope erosion hazard in a large area. The methods and results described in this previous work are important in understanding the spatio-temporal dynamics of hillslope erosion and ground cover. According to Kinnell (2014), run-off production, which is spatially uniform, is often inappropriate under natural conditions because infiltration is spatially variable. Upslope length varies with the ratio of the upslope run-off coefficient to the run-off coefficient for the area below the downslope boundary of the segment in the modified RUSLE approach. The use of upslope length produces only minor variations in soil loss compared with the use of values predicted by the standard RUSLE approach when the run-off is spatially variable and the number of segments increases. By contrast, the USLE-M approach can predict soil loss that is influenced strongly by run-off when run-off varies in space and time. Therefore, an increase in run-off through a segment causes an increase in soil loss, and a decrease in run-off through a segment or cell results in a decrease in soil loss.
In general, past studies (e.g. Tresch et al., 1995; Rick et al., 2001; Silburn, 2011; Yang, 2014; Kinnell, 2014; Shi et al., 2004; Xiao et al., 2004) focused on sloping fields, but the research on soil erosion on highway slopes is limited. A subgrade slope is a major part of soil erosion during construction and operation periods. Therefore, soil erosion caused by a subgrade slope should be predicted. However, the research on soil loss of highways hardly meets the requirements of practical work (Xu et al., 2009; Bakr et al., 2012). We still need to conduct considerable work on the prediction of soil erosion on highway slopes. The situation in various regions in China indicates that researchers have helped improve the RUSLE model and studied soil erosion in certain areas. Water and soil erosion caused by engineering construction is an important aspect of research, especially from the perspective of agricultural cultivation and forestry deforestation because the amount of eroded soil produced by embankment slopes accounts for a large proportion of the entire project area. Although this concern is related to project feasibility and cost in particular, the topic has elicited considerable interest in general. Furthermore, the principal factor that causes soil erosion on slopes generally corresponds to precipitation amount and embankment width. Wang et al. (2005) established several experimental standardised spots for soil loss collection on the side slopes of the Xiaogan–Xiangfan Freeway (i.e. under construction thus far) and installed an on-the-spot rainfall auto-recorder. The collected data were used for the revision of the main parameters R (rainfall and run-off) and K (erodibility of soil) of USLE, which is widely applied to forecast soil loss quantity in ploughland and predict the soil loss quantities of different types of soil on side slopes disturbed by engineering measures (Wang et al., 2005). This method not only applies to the prediction of disturbed soil loss during expressway construction but also improves prediction accuracy. It also provides scientific support for relevant units or personnel to implement reasonable preventive measures.
Related literature indicates that research on soil loss in highways has the following limitations. First, most of the studies on C and P factors that used the RUSLE model were conducted by referring to previous research results, and data accuracy is often poor. Second, most studies on rainfall erosivity (R) factors are limited to sloping fields, and the rainfall erosivity factors of expressway slopes in mountain areas have rarely been studied. Third, slope soils in highways differ depending on soil arability, and the slopes also vary. Thus, accurately predicting the soil loss of different types of subgrade slopes using the traditional K factor calculation method is difficult.
Previous studies have shown that the spatial interpolation method of precipitation is unsuitable for the study of the spatio-temporal distribution of precipitation in mountain areas (Liu and Zhang, 2006). The problem involves two aspects. From the timescale perspective, the characteristics of rainfall distribution and the influencing factors are not fully considered. From the spatial-scale perspective, the spatial heterogeneity of the region is ignored. Furthermore, many studies have limited the factors that affect precipitation to altitude factors, leading to low interpolation accuracy (Zhao et al., 2011; Liu et al., 2010). Thus, in this study, we consider the spatial heterogeneity of linear engineering of the expressway. The rainfall factor is spatially interpolated to compensate for the following limitations: shortage of rainfall data on mountain areas, difficulty of representing the rainfall data of an entire expressway using data from a single meteorological station, and uneven spatial distribution and strong heterogeneity of rainfall in mountain areas (Li et al., 2017). We analyse the characteristics of soil erosion to improve certain aspects of expressway construction on the basis of previous research. We divide a highway slope into natural and artificial units and calculate the amount of soil loss from the slope surface to the pavement based on the slope surface catchment unit. The findings can be popularised because this approach is in line with the actual situation. Next, we modify the parameters of the artificial slope through an actual survey, run-off plot observation, and other methods, and the parameters of the artificial slope are corrected by referring to the form of the project and the utilised materials. We not only scientifically predict the amount of soil erosion caused by highway construction in mountain areas but also provide a scientific basis for the prevention and control of soil erosion and rational allocation of prevention and control measures. The safe operation of highways and the virtuous cycle of the ecological environment should be ensured to promote the sustainable development of the local economy.
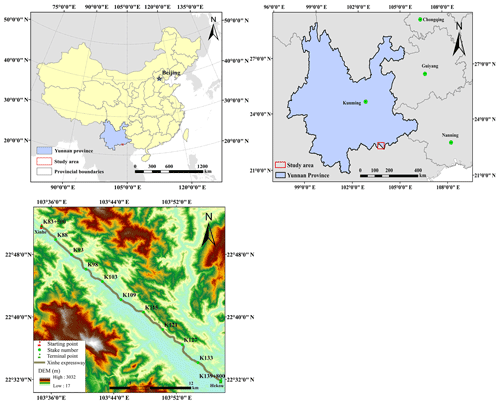
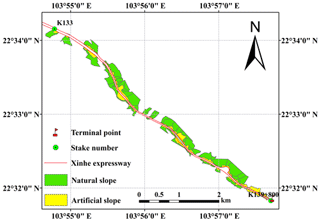
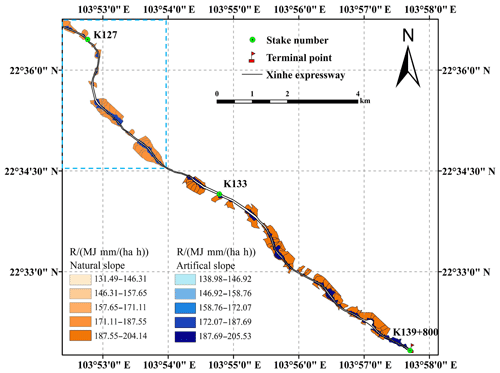
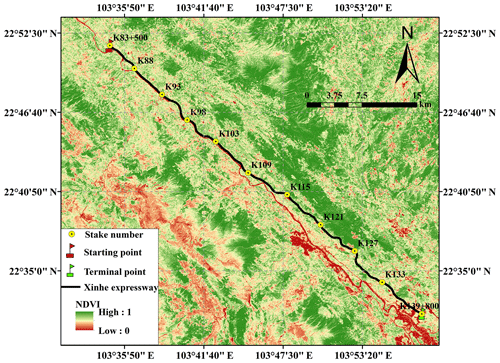
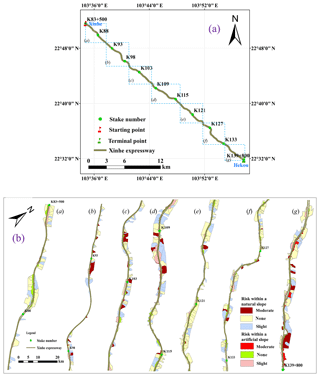
Xinhe Expressway is in the southern margin of the Yunnan–Guizhou Plateau, which is in the south-east of Yunnan Province, Honghe Prefecture, and Hekou Yao Autonomous County. This highway was the first in Yunnan to cross the border. Thus, it has become an important communication channel between China and Vietnam and possesses an important strategic and economic value. The highway is at east longitude 103∘33′45–103∘58′32 and north latitude 22∘31′19–22∘51′48 (Fig. 2) The expressway stretches roughly from north-west to south-east, and its total length is 56.30 km. The climate type belongs to subtropical mountain, seasonal monsoon forest, and humid heat climate categories. Between May and the middle of October, the area experiences a wet season characterised by abundant rainfall, concentrated precipitation, and increased rain at night-time; the variation of precipitation is 400–2000 mm, whilst most regions have 800–1800 mm (Fei et al., 2017; Zhang et al., 2017). During the rest of the year, the area experiences a dry season. The starting point of Xinhe Expressway is in Hekou Yao Autonomous County, New Street (pile number K83+500), at an altitude of 296 m. The endpoint is in the estuary of the village of Areca (pile number K139+800) at an altitude of 95 m. The mountains along both sides are 200–380 m a.s.l. The topography of the hilly area in the northern part of Xinhe Expressway is complicated. The slopes on both sides rise and fall, and most of the valleys constitute V- and U-shaped sections. The natural slopes on both sides are mostly below 57.7 %. The southern part of the highway has a relatively flat terrain and a gentle slope. The slopes of most hills on both sides are less than 26.8 %, and the overall height difference is less than 100 m. The vegetation in the southern part of Xinhe Expressway includes tropical rainforests and tropical monsoon forests, whilst that in the northern part of China is classified as south subtropical monsoon evergreen broad-leaved forest. In recent years, the original vegetation in this area has been reclaimed as farmland and is now planted with rubber, banana, pineapple and pomegranate, which are sporadic tropical rainforest survivors. The project area along Xinhe Expressway is an economic forest belt with a single vegetation type and mainly has rubber, forest, and other economic trees. The soil types along the highway are rich and mainly comprise red, leached cinnamon, grey forest, and grey cinnamon soils.
3.1 Data sources
Rainfall data from 2014 were obtained from Hekou Yao Autonomous County, Pingbian Miao Autonomous County, Jinping Miao Yao Autonomous County, and the meteorological department of Mengzi. The rainfall data were obtained at 5 min intervals. Meanwhile, two automatic weather stations were established along Xinhe Expressway to gather weather data during the 2014 experiment. Meteorological data, which were provided by the China Meteorological Data Network, covered the period of 1959–2015 (http://data.cma.cn/site/index.html, last access: 27 February 2019).
Data on soil types were provided by the Yunnan Traffic Planning and Design Institute. Data on soil texture and organic matter were obtained via field surveys, data sampling, and processing methods. Soil samples were initially collected at each 1 km range of the artificial and natural slopes on both sides of the highway. Five mixed soil samples were obtained from one slope using the S-shaped sampling method (Shu et al., 2017). Then, the method of coning and quartering was adopted (Oyekunle et al., 2011), and half of the mixed soil samples were brought to the laboratory for analysis. Finally, 186 soil samples were obtained. After the soil samples were dried and sieved, soil texture and organic carbon content were measured via specific gravity speed measurement and potassium dichromate external heating, respectively.
The topographic map and design drawings of Xinhe Expressway were provided by the Yunnan Traffic Planning and Design Institute. The 1:2000 scale of the topographic map coordinate system was based on the 2000 GeKaiMeng urban coordinate system, the elevation system for 1985 national height data, and the format for the CAD map in DWG. The remote sensing images used in this study were derived from 8 m hyperspectral images produced by the GF-1 satellite (http://www.rscloudmart.com/, last access: 26 February 2019).
3.2 Prediction model selection
The RUSLE equation (Renard et al., 1997) was used to predict soil and water loss on the side slopes of Xinhe Expressway. The RUSLE equation considers natural and anthropogenic factors that cause soil erosion to produce comprehensive results. The parameters are easy to calculate, and the calculation method is relatively developed. The RUSLE model is suitable for soil erosion prediction in areas where physical models are not required. Equation (1) is expressed as
where A is the average soil loss per unit area by erosion (t ha−1 yr−1), R is the rainfall erosivity factor (MJ mm (ha h yr)−1), K is the soil erodibility factor (t ha h (ha MJ mm)−1), L is the slope length factor, S is the steepness factor, C is the cover and management practice factor, and P is the conservation support practice factor. The values of L, S, C, and P are dimensionless.
3.3 Division and implementation of the prediction unit
Geological structures and rock and soil categories are complex because of considerable changes in topography and physiognomy. The forms of slopes also vary. In general, according to the relationship between slope and engineering, slopes can be natural or artificial. Artificial slope formations can be subdivided into slope embankments and cutting slopes. In this study, we used ArcGIS software to convert the topographic map of the highway design into a vectorisation file because the artificial and natural slopes of watershed catchments are the main components of soil erosion prediction. On the basis of the extracted graphical units, the natural and artificial slopes were divided into uniform prediction units according to aspect, slope, land use, and water conservation measures. The aspect, slope, land use, water conservation measures, and other attributes of each prediction unit were consistent.
4.1 Natural slope catchment area
The catchment unit of the slope was initially constructed using the structural plane tools of ArcGIS combined with ridge and valley lines and artificial slope and highway boundaries (Zerihun et al., 2018). After the completion of the catchment unit, the slope was divided according to soil type data (Table 1). After the division and overlaying of the remote sensing image map, the land use types and soil and water conservation measures were considered as indicators for the visual interpretation of the field survey results and for further classification of the confluence units. The partition units were amended using the vegetation coverage data obtained along Xinhe Expressway. A total of 814 natural slope catchment prediction units were divided.
The artificial slope was divided into roadbed and cutting slopes according to the design of Xinhe Expressway (i.e. 1:1.5 and 1:1.0 slopes). After the preliminary division, the slope measurements, data design, and field survey results were used as a basis for the subsequent detailed division of the artificial slope into cement frame protection and six arris brick revetments. McCool (1987) stated that slope length can vary within a 10 m range and only has a small effect on results. The specifications of each frame in the cement frame protection along Xinhe Expressway were the same. The horizontal projection length of a cement frame can be regarded as the slope length value of an artificial slope. Therefore, the slope length of the artificial slope of each frame of the cement revetment was considered the same, and the value was set to 0. According to investigations, the vegetation coverage of artificial slopes with different plant species varies substantially. To achieve an accurate prediction of unit division and improve prediction accuracy, the artificial slopes should be continuously classified according to plant species. Thus, 422 artificial slope prediction units were obtained. The data of the 1236 slope prediction units were edited using GIS. The results are shown in Fig. 3.
4.2 Determination of conventional parameters of the RUSLE model
4.2.1 Rainfall erosivity factor (R)
The formula of the R value (rainfall erosivity) was adopted (Liu et al., 1999; Shamshad et al., 2008; Wang and Zhang, 1995, Yang et al., 1999; Panagos et al., 2017; Angulo-Martínez and Beguería 2009; Panagos et al., 2015) and calculated using 30 min rainfall intensity as the measure, as shown in Eqs. (2) and (3).
where R is rainfall erosivity (MJ mm (ha h)−1), P is sub-rainfall (mm), and I30 is the maximum 30 min intensity of the storm (mm h−1).
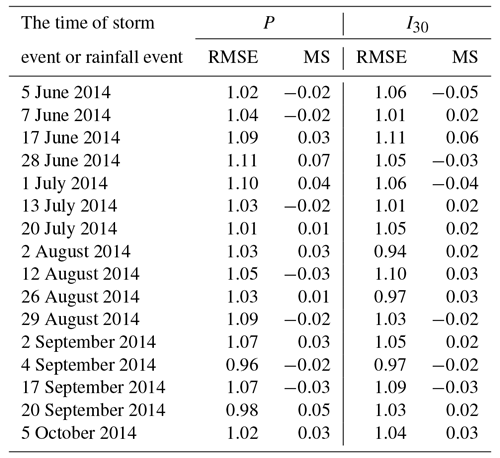
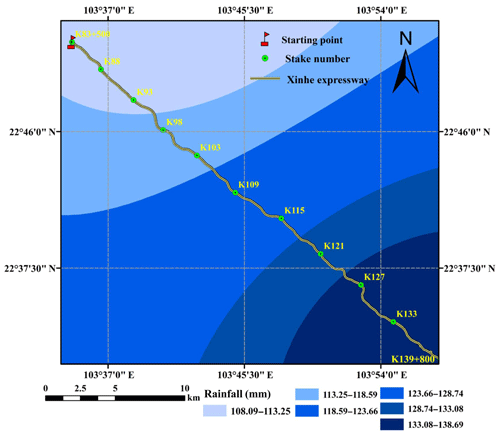
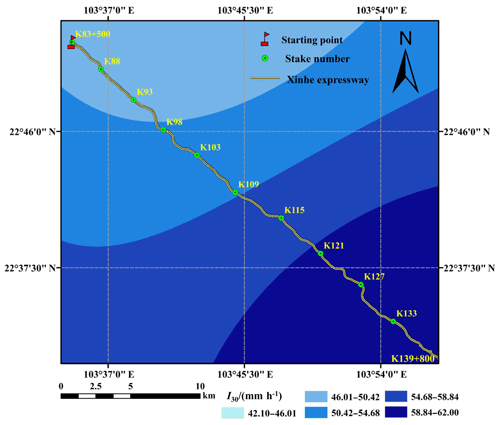
Rainfall data were acquired from stationary ground meteorological stations. However, using data from a single meteorological station to represent the rainfall data of a linear mountain expressway is difficult. The P and I30 values along the highway were obtained by co-kriging calculations. The dataset included the following: rainfall data; 30 min rainfall data from the four meteorological stations in Hekou Yao Autonomous County, Pingbian Miao Autonomous County, Jinping Miao Yao Autonomous County, and Mengzi; and data acquired from two automatic weather stations along the highway. Then, the cross-validation method was used to evaluate the accuracy of the interpolation results. The selection criteria included the standard root mean square error and the mean standard error. The detailed results are shown in Table 2. However, this work only shows the interpolated results of secondary rainfall of two rainfall events and the 30 min rainfall intensity data, as shown in Fig. 4a and b.
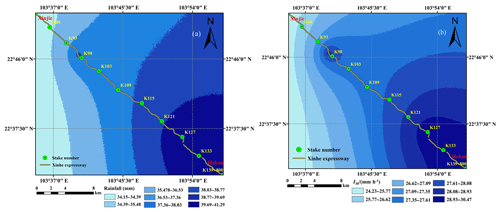
Figure 4(a) Interpolation results of secondary rainfall for 5 June 2014. (b) Interpolation results of I30 for 5 June 2014.
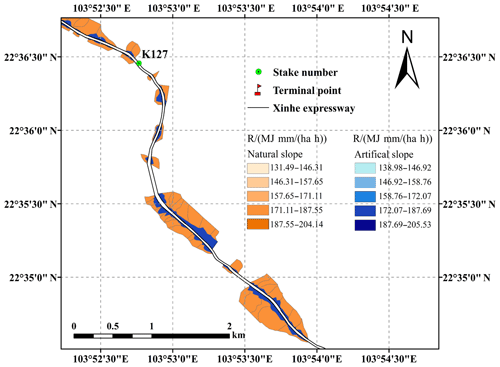
The secondary rainfall data of 16 rainfall instances along Xinhe Expressway were obtained by interpolation because the values for internal rainfall and the rainfall intensity of a single prediction unit are the same. Therefore, the R value was calculated using the average rainfall and rainfall intensity of the unit. Only the spatial distribution map of the rainfall erosivity factors in certain sections (5 June 2014) is shown because of space constraints (Figs. 5 and 6).
4.2.2 Soil erodibility factor (K)
The soil data of a slope in each section were obtained by sampling according to the spatial distribution map of soil types in the study area and by dividing the linear distribution of the soil. The K value was calculated by applying Eq. (4) to obtain the soil erodibility factor values of each slope (Sharpley and Williams, 1990) (Tables S3 and S4 in the Supplement).
In the formula, SAN, SIL, CLA, and C represent sand grains (0.05–2 mm), powder (0.002–0.05 mm), clay (<0.002 mm), and organic carbon content (%), respectively; .
4.2.3 Calculation of topographic factors in natural slope catchments
Slope length factor
On the basis of the topographic map (1:2000 scale) and highway design of Xinhe Expressway, the slope length factor of the slope catchment was calculated using DEM data with 0.5 m spatial resolution generated by ArcGIS. The natural slope catchment was divided into less than 1 %, 1 %–3 %, 3 %–5 %, and greater than or equal to 5 % using the “reclassify” tool in ArcGIS. The L factor algorithm of Moore and Burch (1986) was utilised in the operation (Eqs. 5 and 6).
where L is normalised to the amount of soil erosion along the slope length of 22.13 m, λ is the slope length, flowacc is the total number of contributing pixels for each pixel that is higher than the pixel, and cell size refers to the DEM resolution (0.5 m); m is a variable length-slope exponent.
Equation (6) is expressed as
where θ is the slope.
Slope factor
The S factor was calculated as follows. If the slope was less than 18 %, then the formula of McCool et al. (1987) was used. If the slope was greater than 18 %, then the formula of Liu et al. (2000) was adopted. Equation (8) is expressed as
The DEM data were processed by ArcGIS to obtain slope data. The slope values of each prediction unit were extracted using the Zonal statistics tool. With the classification tool in ArcGIS, the slope of the highway catchment of Xinhe was divided into less than 9 %, 9 %–18 %, and greater than or equal to 18 %.
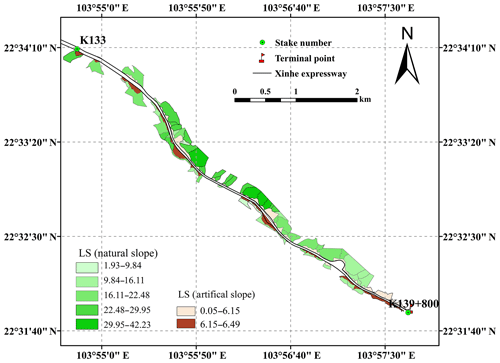
The S values of the slope catchments under the three slope grades were calculated by combining Eq. (8) with ArcGIS techniques. The LS values of the slope prediction units are shown in Fig. 7.
4.2.4 Calculation of topographic factors of artificial slopes
Slope length factor
The method of Z. W. Chen et al. (2010) was used for the calculation of the LS factor of the artificial slopes, and the calculation method for the topographic factors of the artificial slopes of Xinhe Expressway was modified. The slope length factor (La) was calculated using Eqs. (5) and (6). The slope length index (ma) was measured by conducting a run-off plot experiment and calculated using Eq. (9).
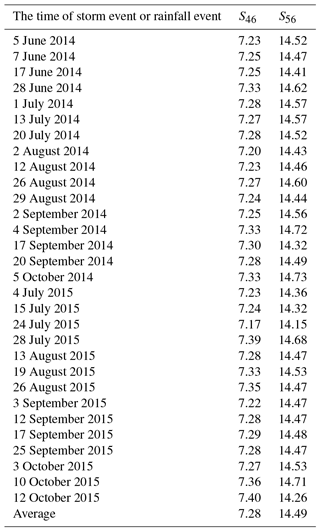
where A1 and A2 are the soil erosion intensity values of two slopes when the slope lengths are λ1 and λ2, respectively (i.e. the specifications of the two slopes are the same except for slope length). The soil erosion amounts under 30 erosion rainfall conditions were monitored in the run-off field of Xiao Xinzhai in Mengzi in 2014–2015 (Table 5). The ma value under each rainfall condition was calculated using Eq. (9) according to the monitoring value of soil erosion amount. The average value of ma was 0.32, and it was regarded as the ma value of the artificial slope length factor (Table 6).
Slope factor
The calculation of the slope factor was based on the method of Z. W. Chen et al. (2010). Six run-off plots were established in the Xiao Xinzhai run-off field of Mengzi. Soil erosion intensity under the slope conditions of 1:1.5, 1:1.0, and 9:100 was monitored. Then, the slope factor for the slope condition was obtained using Eq. (10).
where S represents the slope factor when the slope is θ, A represents the soil erosion intensity (t ha−1) when the slope is θ, and A represents the soil erosion intensity (t ha−1) when the slope is 9 %. The three slope conditions (1:1.5, 1:1.0, and control slope of 9:100) in the soil erosion monitoring experiment were combined with Eq. (10) to calculate the slope factor values of the two slopes (1:1.5 and 1:1.0) under 30 rainfall conditions. The average factors of the slopes under the 1:1.5 and 1:1.0 slope conditions were 7.28 and 14.49, respectively (Table 7).
After the slope design drawings were digitised by ArcGIS, the slope and length values of each artificial slope prediction unit were determined according to design specifications. The slope length value of each artificial slope prediction unit was regarded as the horizontal projection length of the cement frame. The slope length of the six arris brick revetments was 0. Equations (5), (6), (9), and (10), in combination with the slope length factor and ma and Sθ values, were used to calculate the value of LS of each artificial slope prediction unit.
4.2.5 Cover and management practice factor
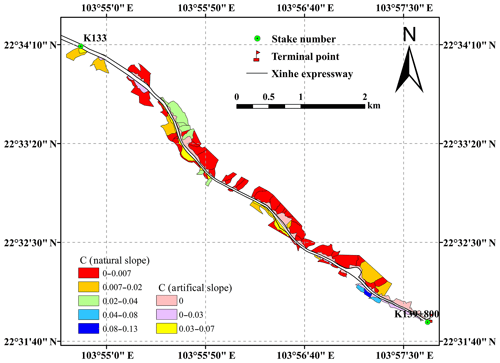
The C factor after topographic analysis is vital in soil loss risk control. In the RUSLE model, the C factor is used to depict the effects of vegetation cover and management practices on the soil erosion rate (Vander-Knijff et al., 2000; Prasannakumar et al., 2011; Alkharabsheh et al., 2013; Feng and Zhao, 2014). The C factor is defined as the loss ratio of soils from cropped land under specific conditions to the corresponding loss from clean-tilled and continuous fallow (Wischmeier and Smith, 1978). Datasets from satellite remote sensing were initially used to assess the C factor due to the various land cover patterns with severe spatial and temporal variations mainly at the watershed scale (Vander-Knijff et al., 2000; Li et al., 2010; Chen et al., 2011; Alexakis et al., 2013). By taking full advantage of NDVI data, C was calculated according to the equation of Gutman and Ignatov (1998) (i.e. Eq. 11). Then, the vegetation coverage data were corrected by examining a sample plot every 2 km along the study area. The algorithm for calculating f was adopted from the work of Tan et al. (2005) (i.e. Eq. 11). Finally, accurate vegetation coverage data were obtained (Fig. 8). The C factor map of the soil erosion prediction unit for the slope catchment area is shown in Fig. 9.
4.2.6 Soil and water conservation measures
The land use types in the natural slope catchment area were classified as cultivated, forest, construction, and difficult-to-use lands. Through a field investigation and visual judgment, the water conservation measures of farmland and forestland were identified as contour belt tillage, horizontal terrace, and artificial slope catchment area, including the cement frame and six arris brick revetments. The P values of the cement frame and the six arris brick revetments, which were determined using the area ratio method, were 0.85 and 0.4, respectively. The P values of the soil and water conservation measures are shown in Table 8.
4.3 Validation of model simulation accuracy
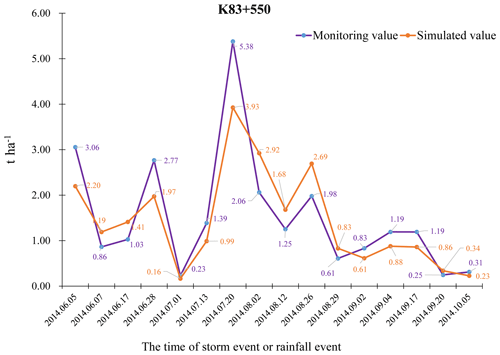
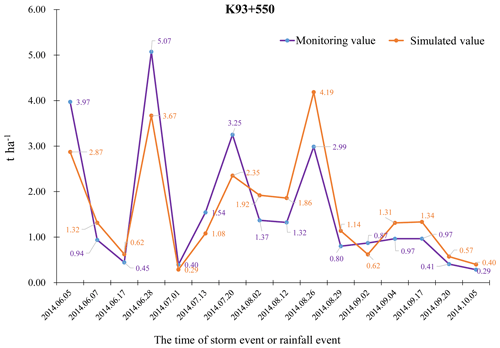
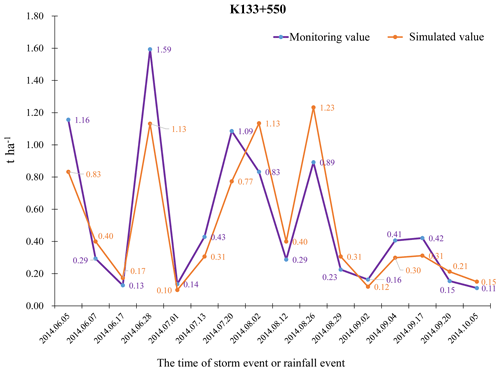
Soil erosion in three monitoring areas under 16 erosive rainfall conditions was monitored in 2014. No rainfall occurred in the 24 h before each rainfall event, and the disturbance of antecedent rainfall on soil erosion on the slopes was excluded. After estimating the historical soil loss of each slope prediction unit, the results were compared with data from the three monitoring plots along the side slope of Xinhe Expressway (Figs. 10–12).
The error analysis showed that the absolute errors of the three monitoring areas under the 16 rainfall conditions were 0.47, 0.53, and 0.16 t ha−1, and the overall average absolute error was 0.39 t ha−1. The average relative errors were 31.80 %, 35.49 %, and 32.26 %, and the overall mean relative error was 31.18 %. The root mean square errors were 0.59, 0.66, and 0.21, all of which were within the acceptable range. The Nash efficiency coefficient of the model was 0.67, which is between 0 and 1, thereby showing that the model's accuracy satisfied the requirements. The calculation results are shown in Tables S10–S12 (Supplement).
The northern and flat terrains of the southern region had a small simulation error because of the high and low areas of the central region of the terrain, which resulted in a slightly lower accuracy than that for the southern region. The absolute error of the simulation was large under heavy rainfall conditions. On the one hand, this result may be caused by the artificial error in sediment collection in the area. On the other hand, the model itself may be defective.
4.4 Application of early warning of soil erosion to the mountain expressway
The rainfall data and I30 values in the 20 years covered by the study were obtained from the meteorological departments of Mengzi, Pingbian Miao Autonomous County, Jinping County, and Hekou Yao Autonomous County in Yunnan Province. Rainfall and its intensity were interpolated by co-kriging, which was introduced into the elevation and geographical position (Figs. 13 and 14).
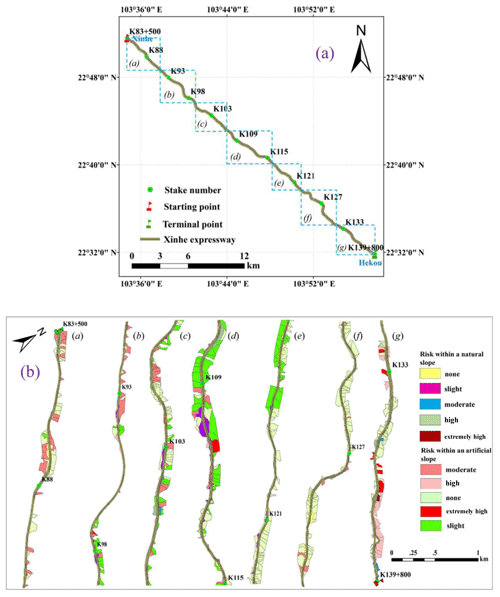
The total soil erosion amount of each prediction unit for the 20-year return period rainfall data was obtained by simulation according to the classification standards of soil erosion intensity. The prediction results were classified as no risk, slight risk, moderate risk, high risk, and extremely high risk (Fig. 15a, b).
The grading results showed that the percentage of prediction units classified as having low and mild risks of soil loss was 88.60 %. Given that the risk of soil erosion is low in these areas, road traffic safety is not affected. The percentage of prediction units classified as having a moderate risk was 4.29 %. The risk of soil erosion in these areas is relatively low under general rainfall intensity conditions. However, with high rainfall intensity, a certain scale of soil erosion disaster could occur. The percentage of prediction units labelled as high risk and extremely high risk was 7.11 %. The risk of soil erosion is high in these units. For example, from K134+500 to K135+500 (1000 m), the average soil erosion amount on both sides of the slope for the 20-year return period rainfall amount reached 17.57 t ha−1. Even if only a portion of the sediment is deposited on the road, road safety will still be affected.
Similarly, the risk of soil erosion was analysed according to the grading standard of soil loss risk under the 20-year return period rainfall condition. This analysis was performed by simulating the soil erosion amount of each prediction unit for the 1-year return period rainfall amount (Fig. 16a, b).
The results indicated that the risk percentages of the prediction units for no soil erosion and mild soil erosion were 78.00 % and 17.92 %, respectively. Given that the risk of soil erosion is low in these areas, the safety of road traffic is not affected. The risk percentage of prediction units for mild soil erosion was 6.08 %. Therefore, the layout of soil and water conservation measures in these areas should be rationally adjusted. Moreover, comprehensive management of their slopes should be strengthened, and plant and engineering measures should be applied comprehensively to conserve soil and water in these regions. Inspections must be reinforced, and motorists should be reminded to focus on traffic safety during rainy seasons. Most of the artificial slopes covered by the study area are made of six arris brick revetments; that is, the amount of soil erosion is small, and the frame-type cement slope protection against soil erosion is sturdier than in other areas. Slope protection measures should be rationally adjusted according to the predicted results. We may adopt ecological slope protection technologies to slow down the roadbed slope and thus keep the slope stable. For example, spraying and planting technology for bolt hanging nets can be used to build a layer of planting matrix that can grow and develop on the weathered rock slope because it can resist the porous and stable structure of the scouring. Technologies for masonry wall maintenance and honeycomb grid revetment protection can also be used. Various other technologies can be adopted to prevent and control soil erosion, and they can beautify the landscape environment of the road area whilst ensuring road traffic safety.
The slope is the main factor of soil loss caused by highways. Thus, the slope is crucial for prediction and early warning systems. A highway slope can be divided into natural and engineering (artificial) slopes, and the RUSLE model can be used to predict soil erosion on natural slopes. Disregarding rainfall erosivity variations, we found that the methods of model parameter acquisition for literature analysis and for comparison of areas of the same type are consistent (Yang 1999, 2002; Peng et al., 2007; Zhao et al., 2007; Chen et al., 2014; Zhu et al., 2016). After comparing the monitoring data with run-off plots, we discovered that the error between the predicted value and the monitoring value calculated by the RUSLE model is negligible (Yang, 1999, 2002; Li et al., 2004). These findings indicate that the prediction results of the model are reliable. In the prediction of erosion on engineering (artificial) slopes, previous studies emphasised surface disturbance during construction (He, 2004, 2008; Liu et al., 2011; Hu, 2016; Zhang et al., 2016; Song et al., 2007) but did not consider soil erosion as a result of the construction. In the process of predicting soil loss in engineering slopes using the RUSLE model, the correction of the conservation support factor (i.e. cement block and hexagonal brick) is often ignored (Zhang, 2011; Morschel et al., 2004; Correa and Cruz, 2010). In addition, most cases use RUSLE modelling to predict the soil erosion on highway slopes. Remote sensing is usually based on grid data and does not consider catchment units (IsIam et al., 2018; Villarreal et al., 2016; Wu and Yan 2014; Y. J. Chen et al., 2010).
In this study, we analysed the characteristics of soil erosion during expressway construction to improve several aspects of previous research. First, we divided the highway slope into natural and artificial units and calculated the amount of soil loss from the slope surface to the pavement based on the slope surface catchment unit. Given that this approach is more in line with the actual situation than previous methods, the findings of the present study can be popularised. Second, we considered the spatial heterogeneity of the linear engineering of an expressway. The rainfall factor was spatially interpolated to compensate for the limitations on rainfall data which were usually evident in previous studies. Third, we modified the parameters of the artificial slope through an actual survey, run-off plot observation, and other methods, and the parameters of the artificial slope were corrected by referring to the form of the project and the utilised materials.
In this study, we used the Revised Universal Soil Loss Equation (RUSLE) as the prediction model for soil loss on slopes, the prediction of soil loss on highway slopes, and the simulation of the risk of soil loss along mountain expressways. We not only scientifically predict the amount of soil erosion caused by highway construction in mountain areas but also provide a scientific basis for the prevention and control of soil erosion and rational allocation of prevention and control measures. The error analysis of the actual observation data showed that the overall average absolute error of each monitoring area was 0.39 t ha−1, the average relative error was 31.18 %, the root mean square error was between 0.21 and 0.66, and the Nash efficiency coefficient was 0.67. The method of soil loss prediction adopted in this work generally has a smaller error and higher prediction accuracy than other models, and it can satisfy prediction requirements. The risk grades of soil loss along the slope of Xinhe Expressway were divided into 20- and 1-year return period rainfall conditions based on simulated predictions. The results showed that the percentage of slope areas with high and extremely high risks was 7.11 %. These areas are mainly located in the K109+500–K110+500 and K133–K139+800 sections. Therefore, relevant departments should strengthen disaster prevention and reduction efforts and corresponding water and soil conservation initiatives in these areas.
Meteorological data, which were provided by the China Meteorological Data Network, covered the period of 1959–2015 and are available at http://data.cma. cn/site/index.html (National Meteorological Information Center, 2019). The remote sensing images used in this study were derived from 8 m hyperspectral images produced by the GF-1 satellite (http://www.rscloudmart.com/, ChinaRS geoinfomatics Co. ltd., 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-19-757-2019-supplement.
SQ and YL conceived and designed the experiments. BL, BC, CM, YQ, and QC performed the experiments. YL, SQ, and BL performed the data analyses and wrote the paper. YL and SQ helped perform the analysis with constructive discussions.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Landslide-road network interactions”. It is not associated with a conference.
This study was jointly supported by the Yunnan Provincial Communications Department Project (2012-272-(1)) and the Yunnan Provincial Science and Technology Commission Project (2014RA074).
This paper was edited by Paolo Tarolli and reviewed by two anonymous referees.
Alexakis, D., Diofantos, G., and Hadjimitsis, A.: Integrated use of remote sensing, GIS and precipitation data for the assessment of soil erosion rate in the catchment area of “Yialias” in Cyprus, Atmos. Res., 131, 108–124, 2013.
Alkharabsheh, M. M., Alexandridis, T. K., Bilasb, G., and Misopolinos, N.: Impact of land cover change on soil erosion hazard in northern Jordan using remote sensing and GIS, Four decades of progress in monitoring and modeling of processes in the soil-plant-atmosphere system: applications and challenges, Procedia Environ. Sci., 19, 912–921, 2013.
Angulo-Martínez, M. and Beguería, S.: Estimating rainfall erosivity from daily precipitation records: a comparison among methods using data from the ebro basin (NE spain), J. Hydrol., 379, 111–121, 2009.
Bakr, N., Weindorf, D. C., Zhu, Y. D., Arceneaux, A. E., and Selim, H. M.: Evaluation of compost/mulch as highway embankment erosion control in louisiana at the plotscale, J. Hydrol., 468, 257–267, 2012.
Bosco, C., de Rigo, D., Dewitte, O., Poesen, J., and Panagos, P.: Modelling soil erosion at European scale: towards harmonization and reproducibility, Nat. Hazards Earth Syst. Sci., 15, 225–245, https://doi.org/10.5194/nhess-15-225-2015, 2015.
Cai, C. F., Ding, S. W., Shi, Z. H., Huang, L., and Zhang, G. Y.: Study of Applying USLE and Geographical Information System IDRISI to Predict Soil Erosion in Small Watershed, J. Soil Water Conserv., 14, 19–24, 2000.
Chen, B. H.: The study on multivariate spatial interpolation method of precipitation in mountainous areas, Beijing Forestry University, 45–48, 2016 (in Chinese).
Chen, F., Zeng, M. G., and Zhou, Z. H.: Evaluation for Ecological Benefits of Greening on Expressways in Mountainous Area, Technology of Highway and Transport, 1, 139–143, 2015 (in Chinese).
Chen, S. X., Yang, X. H., Xiao, L. L., and Cai, Y. H.: Study of Soil Erosion in the Southern Hillside Area of China Based on RUSLE Model, Resources Science, 36, 1288–1297, 2014 (in Chinese).
Chen, T., Niu, R. Q., Li, P. X., Zhang, L. P., and Du, B.: Regional soil erosion risk mapping using RUSLE, GIS, and remote sensing: a case study in miyun watershed, north china, Environ. Earth Sci., 63, 533–541, 2011.
Chen, Y. J., Sun, K. M., and Zhao, Y.: Experiment on the effect of rule caused by slope angle on sand and runoff under the condition of ecological protected slope, Journal of Water Resources and Water Engineering, 21, 55–59, 2010 (in Chinese).
Chen, Z. W., He, F., and Wang, J. J.: Revises of Terrain Factors of Roadbed Side Slope in Universal Soil Loss Equation, Highway, 12, 180–185, 2010 (in Chinese).
ChinaRS geoinfomatics Co. ltd.: Data Center, available at: http://www.rscloudmart.com/, last access: 28 March 2019.
Correa, C. M. C. and Cruz, J.: Real and estimative erosion through RUSLE from forest roads in undulated at heavily undulated relief, Revista Árvore, 34, 587–595, 2010.
Cunha, E. R. D., Bacani, V. M., and Panachuki, E.: Modeling soil erosion using RUSLE and GIS in a watershed occupied by rural settlement in the Brazilian Cerrado, Nat. Hazards, 85, 1–18, 2017.
Dong, H. and Zeng, H.: Discussion on the current situation and the future of China highway construction, Technology and Economy in Areas of Communication, 5, 17–18, 2003 (in Chinese).
Fei, X. H., Song, Q. H., Zhang, Y. P., Liu, Y. T., Sha, L. Q., Yu, G. R., Zhang, L. M., Duan, C. Q., Deng, Y., Wu, C. S., Lu, Z. Y., Luo, K., Chen, A. G., Xu, K., Liu, W. W., Huang, H., Jin, Y. Q., Zhou, R. W., and Grace, J.: Carbon exchanges and their responses to temperature and precipitation in forest ecosystems in Yunnan, Southwest China, Sci. Tot. Environ., 616, 824–840, 2017.
Feng, Q. and Zhao, W. W.: The study on cover-management factor in USLE and RUSLE: a review, Acta Ecologica Sinica, 34, 4461–4472, 2014 (in Chinese).
Fenta, A. A., Yasuda, H., Shimizu, K., Haregeweyn, N., and Negussie, A.: Dynamics of Soil Erosion as Influenced by Watershed Management Practices: A Case Study of the Agula Watershed in the Semi-Arid Highlands of Northern Ethiopia, Environ. Manage., 58, 1–17, 2016.
Foster, G. R., Weesies, G. A., McCool, D. K., Joder, D. C., and Renard, K. G.: Revised Universal Soil Loss Equation User's Manual, Gov. Print. Office, Washington DC, p. 48, 1999.
Gong, J. and Yang, P.: Study on the Layout of Soil and Water Conservation Monitoring Sites during the Construction of Mountain Highways-Case Study of Enlai, Enqian Highway, Subtropical Soil and Water Conservation, 28, 9–11, 2016 (in Chinese).
He, F.: Prediction of soil erosion in foundation slope of South Hubei Road Based on RUSLE, Beijing Normal University, 45–50, 2008 (in Chinese).
He, X. W.: Study on prediction of soil erosion in Road area. Beijing Normal University, 30–34, 2004 (in Chinese).
Hu, L.: Study on development and mechanism of water Erosion and Ecological water erosion control technology of Highway slope in Cold Region, Xi'an University of technology, 56–58, 2016 (in Chinese).
Islam, M. R., Wan, Z. W. J., Lai, S. H., Osman, N., Din, M. A. M., and Zuki, F. M.: Soil erosion assessment on hillslope of GCE using RUSLE model, J. Earth Syst. Sci., 127, 50, https://doi.org/10.1007/s12040-018-0951-2, 2018.
Jia, Y. H., Dai, D. C., and Liu, Y.: Performance Analyse and Evaluation of Freeway in China, Journal of Beijing Jiaotong University, 29, 1–5, 2005 (in Chinese).
Jia, Z. R. and Guo Z. Y.: Quantifying Evalution Approach to Highway Soil Bioengineering, Research of Soil and Water Conservation, 15, 260–262, 2008 (in Chinese).
Jiang, M., Pan, X. Y., and Nie, W. T.: Preliminary analysis of prevention and control of soil and water loss in expressway project construction, Yangtze River, 48, 61–64, 2017 (in Chinese).
Kateb, H. E., Zhang, H. F., Zhang, P. C., and Mosandl, R.: Soil erosion and surface runoff on different vegetation covers and slope gradients: A field experiment in Southern Shaanxi Province, China, Catena, 105, 1–10, 2013.
Kinnell, P. I. A.: Applying the RUSLE and the USLE-M on hillslopes where runoff production during an erosion event is spatially variable, J. Hydrol., 519, 3328–3337, 2014.
Li, J. G., Dao, H. Y., Zhang, L., and Zhang, H. K.: Soil and Water Loss Monitoring in the Dianchi Watershed, Research of Soil and Water Conservation, 11, 75–77, 2004 (in Chinese).
Li, Y., Qi, S., Cheng, B. H., Ma, J. M., Ma, C., Qiu, Y. D., and Chen, Q. Y.: A Study on Factors of Space-time Distributions of Precipitation in Ailao Mountain Area and Comparison of Interpolation Methods, Earth Env., 45, 600–610, 2017 (in Chinese).
Lin, H. L., Zheng, S. T., and Wang, X. L.: Soil erosion assessment based on the RUSLE model in the Three-Rivers Headwaters area, Qinghai-Tibetan Plateau, China, Acta Prataculturae Sinica, 26, 11–22, 2017 (in Chinese).
Liu, B. Y., Nearing, M. A., Shi, P. J., and Jia, Z. W.: Slope length effects on soil loss for steep slopes, Soil Sci. Soc. Am. J., 64, 1759–1763, 2000.
Liu, J. T. and Zhang, J. B.: Interpolation analysis of the spatial distribution of precipitation in mountain area, J. Irrig. Drain. E., 25, 34–38, 2006 (in Chinese).
Liu, S. L., Zhang, Z. L., Zhao, Q. H., Deng, L., and Dong, S. K.: Effects of Road on Landscape Pattern and Soil Erosion: A Case Study of Fengqing County, Southwest China, Chinese Journal of Soil Science, 42, 169–173, 2011 (in Chinese).
Liu, W. Y.: Preliminary Study on R Index of Zhaotong Basin, Yunnan Forestry Science and Technology, 2, 24–26, 1999 (in Chinese).
Liu, X. Y.: Study on the slope stability and its rheological influence in Mountain highway, Central South University, 49–53, 2013 (in Chinese).
Liu, Z. Y., Zhang, X., and Fang, R. H. Analysis of spatial interpolation methods to precipitation in Yulin based on DEM, Journal of Northwest A&F University, 38, 227–234, 2010 (in Chinese).
McCool, D. K., Brown, L. C., Foster, G. R., Mutchler, C. K., and Meyer, L. D.: Revised slope steepness factor for the universal soil loss equation, T. ASAE, 30, 1387–1396, 1987.
Millward, A. A. and Mersey, J. E.: Adapting the rusle to model soil erosion potential in a mountainous tropical watershed, Catena, 38, 109–129, 1999.
Molla, T. and Sisheber, B.: Estimating soil erosion risk and evaluating erosion control measures for soil conservation planning at Koga watershed in the highlands of Ethiopia, Solid Earth, 8, 13–25, https://doi.org/10.5194/se-8-13-2017, 2017.
Moore, I. D. and Burch, G. J.: Physical basis of the length-slope factor in the universal soil loss equation, Soil Sci. Soc. Am. J., 50, 1294–1298, 1986.
Mori, A., Subramanian, S. S., Ishikawa, T., and Komatsu, M.: A Case Study of a Cut Slope Failure Influenced by Snowmelt and Rainfall, Procedia Engineer., 189, 533–538, 2017.
Morschel, J., Fox, D. M., and Bruno, J. F.: Limiting sediment deposition on roadways: topographic controls on vulnerable roads and cost analysis of planting grass buffer strips, Environ. Sci. Pol., 7, 39–45, 2004.
National Meteorological Information Center: Daily Data Set of Surface Climate Data in China, available at: http://data.cma.cn/site/index.html, last access: 28 March 2019.
Panagos, P., Ballabio, C., Borrelli, P., Meusburger, K., Klik, A., Rousseva, S., Tadi'c, M. P., Michaelides, S., Hrabalíková, M., Olsen, P., Aalto, J., Lakatos, M., Rymszewicz, A., Dumitrescu, A., Beguería, S., and Alewell, C.: Rainfall erosivity in Europe, Sci. Total Environ., 511, 801–814, 2015.
Panagos, P., Borrelli, P., Meusburger, K., Yu, B., Klik, A., Lim, K. J., Yang, J. E., Ni, J., Miao, C., Chattopadhyay, N., Sadeghi, S. H., Hazbavi, Z., Zabihi, M., Larionov, G. A., Krasnov, S. F., Gorobets, A. V., Levi, Y., Erpul, G., Birkel, C., Hoyos, N., Naipal, V., Oliveira, P. T. S., Bonilla, C. A., Meddi, M., Nel, W., Al Dashti, H., Boni, M., Diodato, N., Van Oost, K., Nearing, M., and Ballabio, C.: Global rainfall erosivity assessment based on high-temporal resolution rainfall records, Sci. Rep.-UK, 7, 4175, https://doi.org/10.1038/s41598-017-04282-8, 2017.
Panagos, P., Standardi, G., Borrelli, P., Lugato, E., Montanarella, L., and Bosello, F.: Cost of agricultural productivity loss due to soil erosion in the European union: from direct cost evaluation approaches to the use of macroeconomic models, Land Degrad. Dev., https://doi.org/10.1002/ldr.2879, 2018.
Panagos, P., Ballabio, C., Borrelli, P., Meusburger, K., Klik, A., Rousseva, S., Tadić, M. P., Michaelides, S., Hrabalíková, M., lsen, P., Aalto, J., Lakatos, M., Rymszewicz, A., Dumitrescu, A., Beguería, S., Alewell, C.: Rainfall erosivity in Europe, Sci. Total Environ., 511, 801–814. https://doi.org/10.1002/ldr.2879, 2015.
Peng, J., Li, D. D., and Zhang, Y. Q.: Analysis of Spatial Characteristics of Soil Erosion in Mountain Areas of Northwestern Yunnan Based on GIS and RUSLE, J. Mt. Sci., 25, 548–556, 2007 (in Chinese).
Prasannakumar, V., Shiny, R., Geetha N., Vijith, H.: Spatial prediction of soil erosion risk by remote sensing, GIS and RUSLE approach: a case study of Siruvani river watershed in Attapady valley, Kerala, India. Environmental Earth Sciences, 64, 965–972, 2011.
Ren, Y. (China.com.cn.): The total mileage of road was 4 773 500 km, the total mileage of highways was 136 500 km in China (EB/OL), http://www.chinahighway.com/news/2018/1183657.php?tdsourcetag=s_pcqq_aiomsg, last access: 24 August 2018.
Renard, K. G., Foster, G. R., Weesies, G. A., McCool, D. K., and Yoder, D. C.: Predicting soil erosion by water-a guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE), United States Department of Agriculture, Agricultural Research Service (USDA-ARS) Handbook No. 703, United States Government Printing Office, Washington, DC, 1997.
Rick, D., Van, R., Matthew, E. H., and Robert J. H.: Estimating the LS Factor for RUSLE through Iterative Slope Length Processing of Digital Elevation Data within Arclnfo Grid, Cartography, 30, 27–35, 2001.
Shamshad, A., Azhari, M. N., Isa, M. H., Hussin, W. M. A. W., and Parida, B. P.: Development of an appropriate procedure for estimation of RUSLE EI30 index and preparation of erosivity maps for Pulau Penang in Peninsular Malaysia, Catena, 72, 423–432, 2008.
Sharpley, A. N. and Williams, J. R.: EPIC-erosion/productivity impact calculator: 2. User manual, Technical Bulletin-United States Department of Agriculture, 4, 206–207, 1990.
Shi, Z. H., Cai, C. F., Ding, S. W., Wang, T. W., and Chow, T. L.: Soil conservation planning at the small watershed level using RUSLE with GIS: a case study in the Three Gorge Area of China, Catena, 55, 33–48, 2004.
Shu, Z. Y., Wang, J. Y., Gong, W., Lv, X. N., Yan, S. Y., Cai, Y., and Zhao, C. P.: Effects of compound management in citrus orchard on soil micro-aggregate fractal features and soil physical and chemical properties, Journal of Nanjing Forestry University (Natural Sciences Edition), 41, 92–98, 2017.
Silburn, D. M.: Hillslope runoff and erosion on duplex soils in grazing lands in semi-arid central Queensland, USLE erodibility (K factors) and cover-soil loss relationships, Soil Res., 49, 127–134, 2011.
Song, F. L., Ma, Y. H., Zhang, C. X., Yu, H. M., Hu, H. X., He, J. L., and Huang, J. Y.: Research progress on greening substrate material of ecological protection of expressway-side slope, Science of Soil and Water Conservation, 6, 57–61, 2008 (in Chinese).
Song, X. Q., Zhang, C. Y., and Liu, J.: Formation of Soil and Water Loss and Its Characteristics in Development and Construction Projects, Bulletin of Soil and Water Conservation, 27, 108–113, 2007 (in Chinese).
Tan, B. X., Li, Z. Y., Wang, Y. H., Yu, P. T., and Liu, L. B.: Estimation of Vegetation Coverage and Analysis of Soil Erosion Using Remote Sensing Data for Guishuihe Drainage Basin, Remote Sensing Technology and Application, 20, 215–220, 2005.
Tan, S. H. and Wang, Y. M.: Research Progress and Thinking of Bioengineering Techniques for Slope Protection in Expressway, Research of Soil and Water Conservation, 11, 81–84, 2004 (in Chinese).
Taye, G., Vanmaercke, M., Poesen, J., Wesemael, B. V., Tesfaye, S., Teka, D., Nyssen, J., Deckers, J., and Haregeweyn, N.: Determining RUSLE P-and C-factors for stone bunds and trenches in rangeland and cropland, North Ethiopia, Land Degradation and Development, 29, https://doi.org/10.1002/ldr.2814, 2017.
Toy, T. J., Foster, G. R., and Renard, K. G.: Soil Erosion: Processes, Prediction, Measurement and Control, 34–44, 2002.
Tresch, S., Meusburger, K., and Alewell, C.: Influence of slope steepness on soil erosion modelling with RUSLE, measured with rainfall simulations on subalpine slopes, Bulletin of Hokkaido Prefectural Agricultural Experiment Stations, 1995.
Vander-Knijff, J. M., Jones, R. J. A., and Montanarella, L.: Soil Erosion Risk Assessment in Europe EUR 19044 EN, Office for Official Publications of the European Communities, Luxembourg, 34 pp., 2000.
Villarreal, M. L., Webb, R. H., Norman, L. M., Psillas, J. L., Rosenberg, A. S., and Carmichael, S.: Modeling landscape-scale erosion potential related to vehicle disturbances along the USA-Mexico border, Land Degrad. Dev., 27, 1106–1121, 2016.
Wang, C. J.: Regional Impaction and Evolution of Express Way Networks in China, Progress in Geography, 25, 126–137, 2006 (in Chinese).
Wang, H. J., Yang, Y., and Wang, W. J.: Prediction of Soil Loss Quantity on Side Slope of Freeway Construction: Amendments to Main Parameters of USLE, Journal of Wuhan University of Technology (Transporatation Science and Engineering), 29, 12–15, 2005 (in Chinese).
Wang, K. and Gao, Z. L.: Analysis of Bioengineering Technology for Slope Protection of Expressway: Taking Expressway from Ankang to the Border of Shaanxi and Hubei as an Example, Ecol. Econ., 31, 155–159, 2015 (in Chinese).
Wang, W. Z. and Zhang, X. K.: Distribution of Rainfall Erosivity R Value in China, Journal of Soil Erosion and Soil Conservation, 2, 7–18, 1995.
Wischmeier, W. H. and Smith, D. D.: Predicting rainfall erosion losses: a guide to conservation planning, in: USDA, Agriculture Handbook No. 537, Washington, DC, 56–62, 1978.
Wischmeier, W. H. and Smith, D. D.: Predicting rainfall-erosion losses from cropland east of the rocky mountains: a guide to conservation planning, 23–30, 1965.
Wu, Y. L. and Yan, L. J.: Impact of road on soil erosion risk pattern based on RUSLE and GIS: a case study of Hangjinqu highway, Zhuji section, Acta Ecologica Sinica, 34, 5659–5669, 2014 (in Chinese).
Xiao, P. Q., Shi, X. J., Chen, J. N., Wu, Q., Yang, J. F., Yang, C. X., and Wang, C. G.: Experimental Study on Protecting Speedway Slope Under Rainfall and Flow Scouring, Bulletin of Soil and Water Conservation, 24, 16–18, 2004 (in Chinese).
Xu, X. L., Liu, W., Kong, Y. P., Zhang, K. L., Yu, B. F., and Chen, J. D.: Runoff and water erosion on road side-slopes: Effects of rainfall characteristics and slope length, Transport. Res. D-Tr. E., 14, 497–501, 2009.
Yang, X.: Deriving rusle cover factor from time-series fractional vegetation cover for hillslope erosion modelling in new south wales, Soil Res., 52, 253–261, 2014.
Yang, Y. C., Wang, M. Z., Xu, Y. Y., Wang, P. C., and Song, Z. P.: Prediction of Soil Erosion on Embankment Slope of Qinhuangdao-Shenyang Special Line for Passenger Trains, J. Soil Water Conserv., 15, 14–16, 2001 (in Chinese).
Yang, Y. and Wang, K.: Discussions on the Side Slope Protection System For Expressway. Industrial Safety and Environmental Protection, 32, 47–49, 2006 (in Chinese).
Yang, Z. S.: Study on Soil Loss Equation of Cultivated Slopeland in Northeast Mountain Region of Yunnan Province, Bulletin of Soil and Water Conservation, 1, 1–9, 1999 (in Chinese).
Yang, Z. S.: Study on Soil Loss Equation in Jinsha River Basin of Yunnan Province, J. Mt. Sci., 20, 3–11, 2002 (in Chinese).
Yoder, D. C., Foster, G. R., Renard, K. G., Weesies, G. A., and McCool, D. K.: C factor calculations in RUSLE, American Society of Agricultural Engineers, Meeting, USA, 55–59, 1993.
Yuan, J. P.: Preliminary Study on Grade Scale of Soil Erosion Intensity, Bulletin of Soil and Water Conservation, 19, 54–57, 1999 (in Chinese).
Zeng, C., Wang, S., Bai, X., Li, Y., Tian, Y., Li, Y., Wu, L., and Luo, G.: Soil erosion evolution and spatial correlation analysis in a typical karst geomorphology using RUSLE with GIS, Solid Earth, 8, 721–736, https://doi.org/10.5194/se-8-721-2017, 2017.
Zerihun, M., Mohammedyasin, M. S., Sewnet, D., Adem, A. A., and Lakew, M.: Assessment of soil erosion using RUSLE, GIS and remote sensing in NW Ethiopia, Geoderma Regional, 12, 83–90, 2018.
Zhang, D. S.: The calculation of urban soil erosion based on GIS-a case study of Wuhan City, Southwest University of M. S. Dissertation, 49–52, 2011 (in Chinese).
Zhang, H., Liao, X. L., and Zhai, T. L.: Evaluation of ecosystem service based on scenario simulation of land use in Yunnan Province, Phys. Chem. Earth, 58–65, https://doi.org/10.1016/j.pce.2017.12.001, 2017.
Zhang, T., Jin, D. G., Tong, G. C., Lin, J., Tang, P., and Li, L. P.: Monitoring Soil Erosion in Linear Production and Construction Project Areas Based on RUSLE – A Case Study of North Ring Expressway in Ningbo City, Zhejiang Province, Bulletin of Soil and Water Conservation, 36, 131–135, 2016 (in Chinese).
Zhao, C. C., Ding, Y. J., Ye, B. S., and Zhao, Q. D.: Spatial distribution of precipitation in Tianshan Mountains and its estimation, Adv. Water Sci., 22, 315–322, 2011 (in Chinese).
Zhao, L., Yuan, G. L., Zhang, Y., He, B., Liu, Z. H., Wang, Z. Y., Li, J.: The Amount of Soil Erosion in Baoxiang Watershed of Dianchi Lake Based on GIS and USLE, Bulletin of Soil and Water Conservation, 27, 42–46, 2007 (in Chinese).
Zhou, F. C.: Highway Slope Ecological Protection Against Erosion Mechanism and Control Effect Research, Chongqing Jiaotong University, 2010 (in Chinese).
Zhou, R. G., Zhong, L. D., Zhao, N. L., Fang, J., Chai, H., Jian, Z., Wei, L., and Li. B.: The Development and Practice of China Highway Capacity Research, Transp. Res. Proc., 15, 14–25, 2016.
Zhu, J., Li, Y. M., and Jiang, D. M.: A Study on Soil Erosion in Alpine and Gorge Region Based on GIS and RUSLE Model-Taking Lushui County of Yunnan Province as an Example, Bulletin of Soil and Water Conservation, 36, 277–283, 2016 (in Chinese).
Zhu, S. Q., Lin, J. L., and Lin, W. L.: Preliminary Study on Effects of Expressway Construction on Side-Slope Soil Erosion in Mountainous Areas, Res. Sci., 26, 54–60, 2004 (in Chinese).
Zhuo, M. N., Li, D. Q., and Zheng, Y. J.: Study on Soil and Water Conservation Effect of Bioengineering Techniques for Slope Protection in Highway, J. Soil Water Conserv., 20, 164–167, 2006 (in Chinese).
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(15850 KB) - Full-text XML
- Corrigendum
-
Supplement
(170 KB) - BibTeX
- EndNote