the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Review article: Review of fragility analyses for major building types in China with new implications for intensity–PGA relation development
James Edward Daniell
Friedemann Wenzel
The evaluation of the seismic fragility of buildings is one key task of earthquake safety and loss assessment. Many research reports and papers have been published over the past 4 decades that deal with the vulnerability of buildings to ground motion caused by earthquakes in China. We first scrutinized 69 papers and theses studying building damage for earthquakes that occurred in densely populated areas. They represent observations where macroseismic intensities have been determined according to the official Chinese Seismic Intensity Scale. From these many studies we derived the median fragility functions (dependent on intensity) for four damage limit states of the two most widely distributed building types: masonry and reinforced concrete. We also inspected 18 publications that provide analytical fragility functions (dependent on PGA, peak ground acceleration) for the same damage classes and building categories. Thus, a solid fragility database based on both intensity and PGA is established for seismicity-prone areas in mainland China. A comprehensive view of the problems posed by the evaluation of fragility for different building types is given. Based on the newly collected fragility database, we propose a new approach in deriving intensity–PGA relations by using fragility as the bridge, and reasonable intensity–PGA relations are developed. This novel approach may shed light on new thought in decreasing the scatter in traditional intensity–PGA relation development, i.e., by further classifying observed macroseismic intensities and instrumental ground motions based on differences in building seismic resistance capability.
- Article
(5840 KB) -
Supplement
(3415 KB) - BibTeX
- EndNote
- Included in Encyclopedia of Geosciences
Field surveys after major disastrous earthquakes have shown that poor performance of buildings in earthquake-affected areas is the leading cause of human fatalities and economic losses (Yuan, 2008). The evaluation of seismic fragility for existing building stocks has become a crucial issue due to the frequent occurrence of earthquakes in the last decades (Rota et al., 2010). Building fragility curves, defined as expected probability of exceeding a specific building damage state under given earthquake ground shaking, have been developed for different typologies of buildings. They are required for the estimation of fatalities and monetary losses due to building structural damage. The development of fragility curves can be divided mainly into two approaches: empirical methods and analytical methods. Empirical methods are based on post-earthquake surveys for groups of buildings and considered to be the most reliable source, because they are directly correlated to the actual seismic behavior of buildings (Maio and Tsionis, 2015). Numerous post-earthquake investigations have been conducted for groups of buildings to derive the empirical damage matrices. A damage matrix is a table of predefined damage states and percentages of specific building types at which each damage state is exceeded due to particular macroseismic intensity levels. However, as pointed out by Billah and Alam (2015), empirical investigations are usually limited to particular sites or seismotectonic/geotechnical conditions with abundant seismic hazard and lack generality. Moreover, they usually refer to the macroseismic intensity, which is not an instrumental measure but is based on a subjective evaluation (Maio and Tsionis, 2015). By contrast, analytical methods are based on static and dynamic nonlinear analyses of modeled buildings, which can produce slightly more detailed and relatively more transparent assessment algorithms with direct physical meaning (Calvi et al., 2006). Therefore, analytical methods are conceived to be more reliable than empirical results (Hariri-Ardebili and Saouma, 2016). Nevertheless, variations in the different practices of analytical fragility studies, such as selection of seismic demand inputs, use of analysis techniques, characterization of modeling structures, definition of damage state thresholds and usage of damage indicators by different authorities, can create discrepancies among various analytical results even for exactly the same building typology. In addition, analytical fragility studies for groups of buildings are computationally demanding and often technically difficult to perform.
Despite the limitations of each fragility analysis method, both empirical and analytical fragility curves are essential in conducting seismic risk assessment. However, the application of the existing fragility curves has been considered to be a challenging task, since different approaches and methodologies are spread across scientific journals, conference proceedings, technical reports and software manuals, hindering the creation of an integrated framework that could allow the visualization, acquisition and comparison between all the existing curves (Maio and Tsionis, 2015). In this regard, the first purpose of this study is to describe and examine available fragility curves, specially developed for Chinese buildings from 87 papers and theses using empirical and analytical methods. The median fragility functions from these previous research findings for the main building types in seismicity-prone areas in mainland China are then outlined.
Furthermore, based on the empirical and analytical fragility database collected, the second purpose of this work is to propose a new approach in deriving intensity–PGA (peak ground acceleration) relations by using fragility as the bridge. The main concern behind this attempt is that the intensity–PGA relation is quite essential in seismic hazard assessment, while traditional practices in deriving such a relation are generally region-dependent and have large scatter (Caprio et al., 2015). Traditionally, intensity–PGA relations are developed using instrumental PGA records and empirical intensity observations within the same geographical range. In this work, we try to establish the intensity–PGA relation using fragility as a conversion medium. Formally, this is achieved by the elimination of the fragility values from the fragility–intensity relation and from the fragility–PGA relation. Theoretically, reasonable results should emerge if the building types used in analytic fragility analyses and those investigated in the empirical field surveys are close enough.
This study is organized as follows. In Sect. 1, the necessity of fragility database construction and the pros and cons of the main fragility analysis methods are briefly introduced. In Sect. 2, a literature review of fragility studies in mainland China and related concepts is provided. Section 3 presents the discrete fragility database extracted from reviewed papers and theses. In Sect. 4, median empirical and analytical fragility curves and their scatter are derived for major building types in seismicity-prone areas in mainland China. In Sect. 5, we introduce in detail our new approach in developing intensity–PGA relations by using fragility as a bridge, which is quite comparable with relations developed by traditional practice. In Appendix and Code and data availability, access to supplementary documents mentioned in the text are provided.
2.1 Empirical method
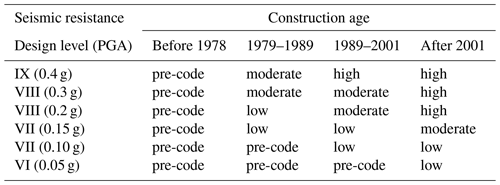
As documented in Calvi et al. (2006), the first application of an empirical method to investigate building fragility at a large geographical scale was carried out in the early 1970s. In mainland China, since the 1975 Haicheng M 7.3 earthquake, around 112 post-earthquake surveys have been conducted for M≥4.7 earthquakes (Ding, 2016). Currently, the main processes in post-earthquake field investigation and macroseismic intensity determination in mainland China basically follow the workflow proposed by Hu (1988) based on the field work on the Tonghai earthquake in the 1970s (Wang et al., 2007). In this workflow, the key concept of “average damage index” is introduced. That means, in each post-earthquake field survey unit (village, town or street), the number of different types of buildings in each damage state are firstly investigated; the median damage index of five damage states, D5, D4, D3, D2 and D1, as defined in GB/T 17742-2008 (2008) is used in later calculation, namely 0.93, 0.70, 0.43, 0.20 and 0.05 for these five damage states, respectively. For each building type in each field survey unit, the corresponding average damage index is derived by summarizing the products of the percentage of building in each damage state and its damage index. Generally, there should be one or two predefined reference building types; thus the average damage index of other surveyed building types can be further scaled to the damage index of the reference building type. In the end, the overall average damage index for each survey unit is calculated by summarizing the products of each building type's scaled damage index and that building type's weight in the survey unit. Once the average damage index in the survey unit is determined, the corresponding macroseismic intensity can be directly derived from the predefined empirical relation between macroseismic intensity and damage index of reference building type (GB/T 17742-2008, 2008). In mainland China, currently three reference building types are used to determine macroseismic intensity: (1) Type A, wood structure, old soil, stone or brick building; (2) Type B, single-story or multistory brick masonry without seismic resistance; (3) Type C, single- or multistory brick masonry sustaining shaking of intensity degree VII. A detailed building structural damage state description for judgment of macroseismic intensity scale in China is given in Table B2 (an unofficial translation of the latest version of the Chinese Seismic Intensity Scale: GB/T 17742-2008, 2008; modified after CSIS, 2019). Comparison of the Chinese Seismic Intensity Scale with other internationally adopted scales was conducted by Daniell (2014) and their relationship is shown in Fig. A1. The correspondence relations between intensity–PGA and intensity–PGV (peak ground velocity) in GB/T 17742-2008 (2008) are also graphically illustrated in Fig. A2 in the Appendix.
Given the importance of building fragility in seismic risk assessment and loss mitigation, in total we reviewed 87 existing fragility analyses from papers and theses for the main building typologies in seismicity-prone areas in mainland China. It is worth noting that, in Ding (2016), a very detailed collection of empirical fragility data was provided for 112 M≥4.7 events since the 1975 M 7.5 Haicheng earthquake based on available post-earthquake surveys. However, due to the lack of building seismic resistance capability information in this database, it is not suitable for our later-on fragility analysis. Thus, we did not use this database and instead collected our own empirical fragility database from individual publications and MS and PhD theses. In mainland China, the main building types of concern are masonry and reinforced concrete (RC) buildings (Sun and Chen, 2009), given the wide distribution of masonry in rural and township areas and the increasing popularity of RC buildings in urban areas. Historic earthquakes that caused serious building damage mainly occurred in seismicity-prone provinces including
-
Sichuan (Chen et al., 2017; Gao et al., 2010; He et al., 2002; Li et al., 2015, 2013; Sun et al., 2013, 2014; Sun and Zhang, 2012; Ye et al., 2017; Yuan, 2008; Zhang et al., 2016),
-
Yunnan (He et al., 2016; Ming et al., 2017; Piao, 2013; Shi et al., 2007; Wang et al., 2005; Yang et al., 2017; Zhou et al., 2007, 2011),
-
Xinjiang (Chang et al., 2012; Ge et al., 2014; Li et al., 2013; Meng et al., 2014; Song et al., 2001; Wen et al., 2017),
-
Qinghai (Piao, 2013; Qiu and Gao, 2015),
-
Fujian (Bie et al., 2010; Zhang et al., 2011; Zhou and Wang, 2015) and
-
other seismic active zones (A, 2013; Chen, 2008; Chen et al., 1999; Cui and Zhai, 2010; Gan, 2009; Guo et al., 2011; Han et al., 2017; He and Kang, 1999; He and Fu, 2009; He et al., 2017; Hu et al., 2007; Li, 2014; Liu, 1986; Lv et al., 2017; Ma and Chang, 1999; Meng et al., 2012, 2013; Shi et al., 2013; Sun and Chen, 2009; Sun, 2016; Wang et al., 2011; Wang, 2007; Wei et al., 2008; Wu, 2015; Xia, 2009; Yang, 2014; Yin et al., 1990; Yin, 1996; Zhang and Sun, 2010; Zhang et al., 2017, 2014; Zhou et al., 2013).
The main outputs of these post-earthquake surveys are empirical damage probability matrices (DPMs), which can be used to derive the discrete conditional probability of exceeding predefined damage limit states under different macroseismic intensity degrees. That is, for the DPMs, macroseismic intensity degree is usually used as the ground motion indicator.
2.2 Analytical method
As summarized in the Introduction section, the main drawback of empirical method lies in the subjectivity on allocating each building to a damage state and the lack of accuracy in the determination of the macroseismic intensity affecting the region (Maio and Tsionis, 2015). Furthermore, the interdependency between macroseismic intensity and damage as well as the limited or heterogeneous empirical data are commonly identified as the main difficulties to overcome in the calibration process of empirical approaches (Del Gaudio et al., 2015). By contrast, analytical methodologies produce more detailed and transparent algorithms with direct physical meaning that not only allow detailed sensitivity studies to be undertaken, but also allow for the straightforward calibration of the various characteristics of the building stock and seismic hazard (Calvi et al., 2006). Different from the empirical fragility that is directly collected from post-earthquake surveys, the derivation of an analytical fragility curve is often based on nonlinear fine-element analysis. Popular analytical methods include pushover analysis (Freeman, 1998, 2004), the adaptive pushover method (Antoniou and Pinho, 2004) and incremental dynamic analysis (IDA) (Vamvatsikos and Cornell, 2002; Vamvatsikos and Fragiadakis, 2010). Within these approaches, most of the methodologies available in literature lie on two main and distinct procedures: the correlation between acceleration or displacement capacity curves and spectral response curves, such as the well-known Hazus or N2 methods (FEMA, 2003; Fajfar, 2000), and the correlation between capacity curves and acceleration time histories, as proposed in Rossetto and Elnashai (2003).
The major steps in using analytical methods to study building fragility include the selection of seismic demand inputs, the construction of building models, the selection of damage indicator and the determination of damage limit state criteria (Dumova-Jovanoska, 2000). To combine empirical post-earthquake damage statistics from actual building groups with simulated and analytical damage statistics from modeled building types under consideration, we examined quite a few studies deriving analytical fragility curves for masonry and RC buildings in mainland China. The analysis techniques in these studies vary from static pushover analysis or the adaptive pushover method (Cui and Zhai, 2010; Liu, 2017), to dynamic history analysis or incremental dynamic analysis (Liu et al., 2010; J. Liu, 2014; Y. Liu, 2014; Sun, 2016; Wang, 2013; Yang, 2015; Yu et al., 2017; Zeng, 2012; Zheng et al., 2015; Zhu, 2010) as well as analysis based on necessary statistical assumptions (Fang et al., 2011; Gan, 2009; Guo et al., 2011; Hu et al., 2010; Zhang and Sun, 2010).
2.3 Damage state definition
As predefined, building fragility describes the exceedance probability of a specific damage state given an ensemble of earthquake ground motion levels. To describe the susceptibility of building structure to a certain ground motion level, four damage limit states are used to discriminate between different strengths of ground shaking: slight damage (LS1), moderate damage (LS2), serious damage (LS3) and collapse (LS4). These four limit states divide the building into five structural damage states, namely negligible (D1), slight damage (D2), moderate damage (D3), serious damage (D4) and collapse (D5). The relation between limit states and structural damage states is illustrated by Fig. 1. Hereafter, fragility curves in this study specifically refer to the probability of exceeding four damage limit states (LS1, LS2, LS3, LS4) under different ground motion levels.
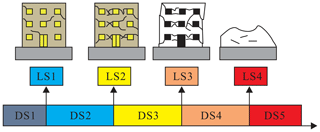
Figure 1Corresponding relation between structural damage states (DS1, D2, D3, DS4, DS5) and limit states (LS1, LS2, LS3, LS4) (modified from Wenliuhan et al., 2015).
Table 1Example of major damage state classification methods (modified after Rossetto and Elnashai, 2003).
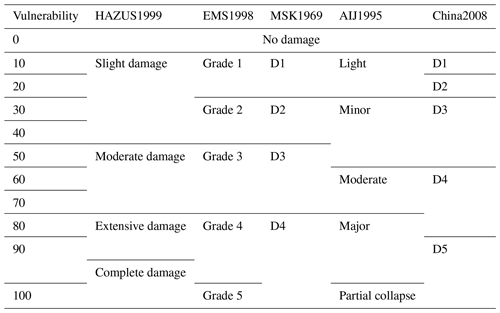
Standard definitions of building structural damage states have been issued in different countries and areas. In the European Macroseismic Scale 1998 (EMS1998, 1998) proposed by the European Seismological Commission (ESC), five grades of structural damage are defined: negligible to slight damage (Grade 1), moderate damage (Grade 2), substantial to heavy damage (Grade 3), very heavy damage (Grade 4) and destruction (Grade 5). In the Hazus 99 Earthquake Model Technical Manual, developed by the Department of Homeland Security, Federal Emergency Management Agency of the United States (FEMA) in 1999, generally four structural damage classes are used for all building types: slight damage, moderate damage, extensive damage and complete damage. Other damage state classifications like MSK1969 proposed by Medvedev and Sponheuer (1969) and AIJ1995 (Nakamura, 1995) in Japan issued by the Architectural Institute of Japan are summarized in Table 1. In mainland China, the latest standard GB/T 17742-2008 (2008) was issued in 2008 by the China Earthquake Administration (CEA), in which detailed damage to structural and nonstructural components is defined for each damage state (Table 2).
Table 2Detailed definition of building damage states in GB/T 17742-2008 (2008), China.
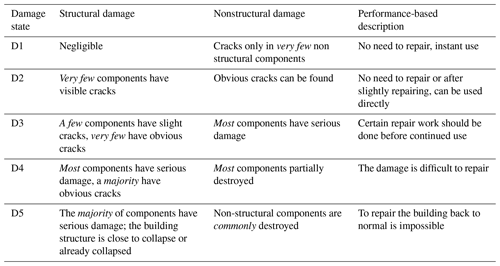
Notes about qualifiers in italics: very few: <10 %; a few: 10 %–50 %; most: 50 %–70 %; majority: 70 %–90 %; commonly: >90 %.
In the empirical method, the fragility curve is derived from damage probability matrices (DPMs) based on post-earthquake field surveys. DPMs give the proportions of buildings in each structural damage state (D1, D2, D3, D4, D5), and they can be used to derive the probability of exceeding each damage limit state P[LSi] (i=1, 2, 3, 4), as illustrated in Eq. (1):
where N refers to the total number of damage limit states (here N=4); for each building type, P[Di] refers to the proportion of building in each structural damage state i.
In the analytical method, the fragility curve is derived by Eq. (2), with the assumption that building response to seismic demand inputs follows the lognormal distribution:
where P[LS|Sd] is the probability of being in or exceeding the damage limit state (LS) due to ground motion indicator Sd (e.g., the inter-story displacement, the spectral acceleration, the peak ground acceleration); SC|LS refers to the median value of the damage state indicator at which the building reaches the threshold of the damage state LS; βLS represents integrated uncertainties from seismic demand input, building capacity and model uncertainty, generally within the range of 0.6–0.8; Φ[] is the normal cumulative probability distribution.
3.1 Building typology and seismic resistance level classification
During the past 4 decades, more than 2000 M≥4.7 earthquakes have occurred in mainland China and its neighboring areas (Xu and Gao, 2014). Up to 2014, post-earthquake field surveys have been conducted for at least 112 damaging earthquakes that occurred in the densely populated areas in mainland China since the 1975 M 7.3 Haicheng earthquake (Ding, 2016). These damaging earthquakes mainly clustered in seismicity-prone provinces in southwestern China (e.g., Sichuan, Yunnan) and western China (e.g., Xinjiang Uygur, Tibet, Qinghai), as shown in Fig. 2. The main building types in these areas feature masonry, reinforced concrete (RC), brick–wood, soil, stone and Chuandou timber (a typical building type in mountainous areas of Tibet, Qinghai and Sichuan). Due to the limitation in fragility data abundance, we mainly focus on studying the seismic fragility of the two most widely distributed building types: masonry and RC (Sun and Chen, 2009). Masonry buildings are mainly composed of brick and concrete. RC buildings include building structures such as RC core walls, frames and frame-shear walls.
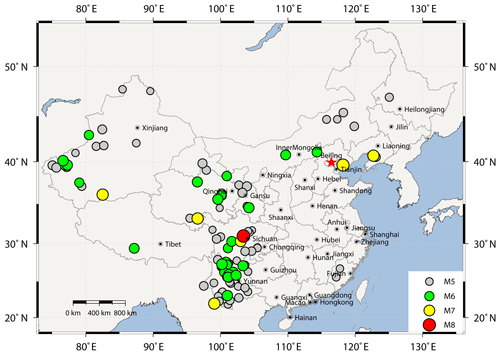
Figure 2The distribution of earthquakes that occurred in mainland China and its neighboring area, for which field surveys were conducted. Detailed earthquake catalogue can be found in the Supplement, which is newly compiled based on Ding (2016) and Xu and Gao (2014). The map was created using Generic Mapping Tools (https://www.generic-mapping-tools.org/, last access: 26 February 2020).
The seismic resistance level of masonry and RC buildings is further divided into two classes: level A and level B. The assignment of seismic resistance level in this study is mainly based on supplementary information given in each scrutinized paper, including building age, construction material, seismic resistance code at construction time, load-bearing structure, etc. Given the changes in building quality and corresponding code standard over the past 4 decades in China, buildings constructed in different ages, though with the same nominal resistance level of each period, are reassigned with different seismic resistance levels according to the latest standard. The referred-to grouping criteria are given in Table 3 (more building classification details can be found in the Supplement). Generally, “level A” includes buildings with seismic resistance level assigned as pre-code, low or moderate, and “level B” includes buildings assigned as high.
3.2 Outlier check
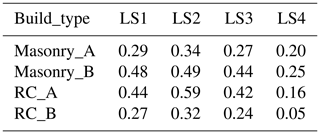
After grouping the empirical and analytical fragilities based on building type (masonry and RC) and seismic resistance level (A and B) in Sect. 3.1, the empirical fragility database based on macroseismic intensity (Fig. 3) and analytical fragility database based on PGA (Fig. 4) for four damage limit states (LS1, LS2, LS3, LS4) are thus constructed (data can be found in the Supplement). The y-axis “fragility” of Figs. 3 and 4 refers to the exceedance probability of each damage limit state at each ground motion level. As can be seen, the scatter of fragilities varies across building types and seismic resistance levels. For empirical fragilities, the scatter may relate to the uneven abundance of damage data for buildings investigated in post-earthquake field surveys, the subjective judgment of damage states and the rough division of building structure types. For analytical fragilities, the scatter may come from the difference in the selection of seismic demand inputs, the use of analysis techniques, the detailing of the modeled building structure, the definition of damage state and the difference in damage indicators used by different researchers. Thus, before deriving consecutive building fragility curves from these discrete fragility data in Figs. 3 and 4, the outliers need to be first removed from these originally collected datasets.
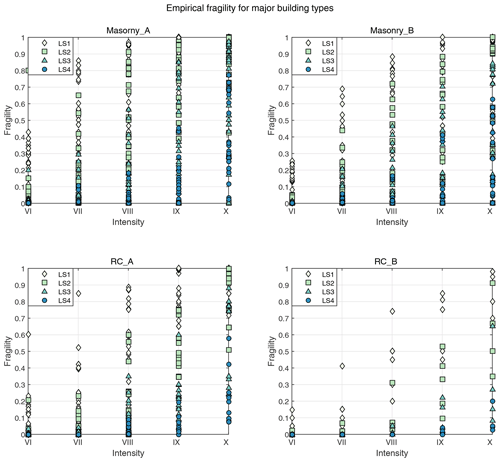
Figure 3The distribution of empirical fragility data from post-earthquake field surveys, depicting the relation between the exceedance probability of each damage limit state (LS1, LS2, LS3, LS4) at given macroseismic intensity levels. The fragility datasets are grouped by building types (masonry and RC) and seismic resistance levels (A and B).
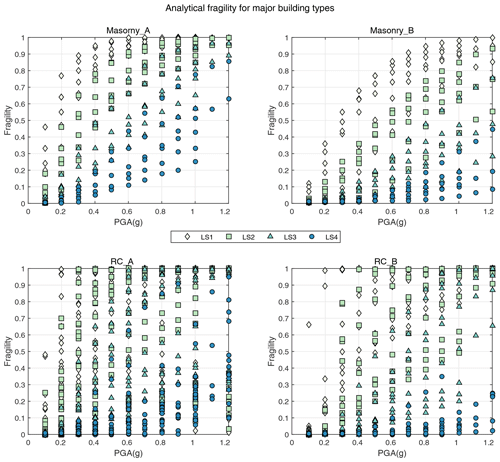
Figure 4The distribution of analytical fragility data derived from nonlinear analyses, depicting the relation between the exceedance probability of each damage limit state (LS1, LS2, LS3, LS4) at given PGA levels. The fragility datasets are grouped by building types (masonry and RC) and seismic resistance levels (A and B).
To figure out the outliers in the originally collected fragility database, the box-plot check method was applied. For each building type (Masonry_A, Masonry_B, RC_A, RC_B) and in each damage limit state (LS1, LS2, LS3, LS4), the corresponding series of fragility data was sorted from the lowest to the highest value. Three quantiles (Q1, Q2, Q3) were used to divide each fragility series into four equal-sized groups and they correspond to the 25 %, 50 % and 75 % quantile value in each series. A discrete fragility value (Qi) was assigned as an outlier if or . The box-plot check results are shown in Fig. 5 for empirical fragility data and in Fig. 6 for analytical fragility data.
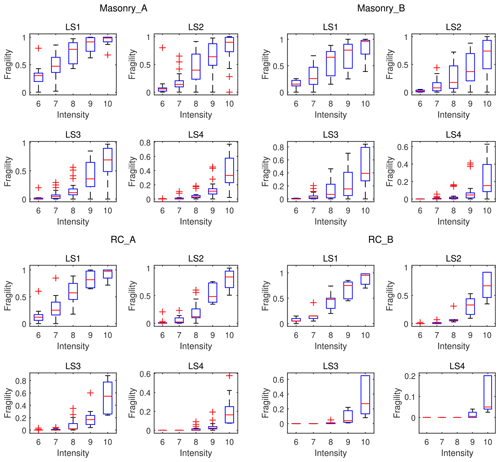
Figure 5Outlier check using the box-plot method for empirical fragility data. Five macroseismic intensity levels are used to classify the original fragility datasets: VI, VII, VIII, IX, X. “A” and “B” represent the pre-code, low and moderate level and the high seismic resistance level, respectively (more classification details are available in the Supplement). LS1, LS2, LS3 and LS4 are the four damage limit states. Outliers are marked by red crosses, and the red line within each box indicates the 50 % quantile fragility value.
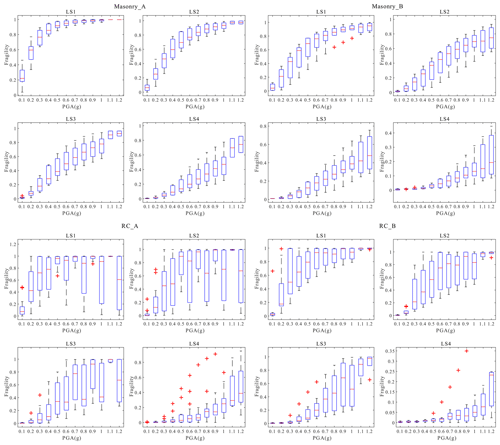
Figure 6Outlier check using the box-plot method for analytical fragility data. Twelve PGA levels are used to group the discrete analytical fragility datasets: 0.1–1.2 g. “A” and “B” represent the pre-, low and moderate level and the high seismic resistance level, respectively (more classification details are available in the Supplement). LS1, LS2, LS3 and LS4 are the four damage limit states. Outliers are marked by red crosses, and the red line within each box indicates the 50 % quantile fragility value.
After removing outliers, details of the remaining fragility dataset (e.g., the number of data points, the median and the standard deviation of these data) for each damage state of each building type are summarized in Appendix Table B1. The change of standard deviation of each fragility series is shown in Figs. A3 and A4 for empirical and analytical data, respectively. It is worth iterating that, as mentioned in the Introduction section, the organization of this study is centered on two focuses. The first one is to construct a comprehensive fragility database for Chinese buildings from 87 papers and theses using empirical and analytical methods, which is one key component of seismic risk assessment. Based on the empirical and analytical fragility database collected, the second focus is to propose a new approach in deriving intensity–PGA relations by using fragility as the bridge. In this regard, a representative fragility curve should be first derived for each damage state of each building type, and we use the median fragility values to derive such a curve.
To derive the representative fragility curve for each damage limit state (LS1, LS2, LS3, LS4) of each building type (Masonry_A, Masonry_B, RC_A, RC_B) for further study (to derive the intensity–PGA relation in Sect. 5), the median values (50 % quantile) of each fragility series in Figs. 5 and 6 are used. For consecutive median fragility curve derivation, cumulative normal distribution is assumed to fit the discrete median empirical fragilities, and lognormal distributions are assumed to fit the discrete median analytical fragilities. For each damage limit state of each building type, the parameters μLS and σLS in the consecutive fragility curve can be regressed following Eq. (3):
or
where P(X|LS) represents the exceedance probability of each damage limit state (LS) given ground motion level X (X refers to Xint, namely macroseismic intensity in terms of empirical fragility, and X refers to XPGA, namely PGA in terms of analytical fragility).
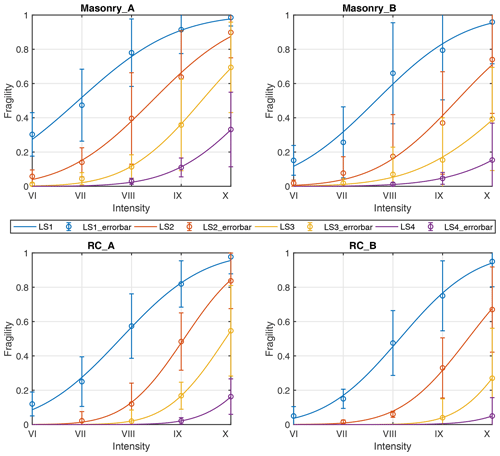
Figure 7Median fragility curve and error-bar analysis derived from empirical fragility datasets, which depicts the relation between macroseismic intensity and exceedance probability of each damage limit state (LS1, LS2, LS3, LS4) for masonry and RC building types (note these median fragility curves are of varying robustness; see Sects. 4 and 5.3 for more details). The circle within each bar represents the median exceedance probability of each damage limit state; the length of each bar indicates the value of the corresponding standard deviation. Only intensity and PGA values with truncated exceedance probability ≥1 % for each damage limit state of each building type are plotted, since higher damage states can appear only for higher intensities or PGA values (see Sect. 5.2 for more details). Detailed values of median fragility and standard deviation are given in Table B1.
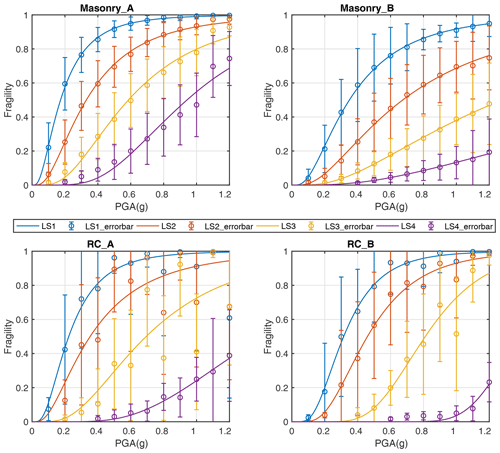
Figure 8Fragility curve and error-bar analysis derived from analytical fragility datasets, which depict the relation between PGAs (unit: g) and exceedance probability of each damage limit state (LS1, LS2, LS3, LS4) for masonry and RC building types (note these median fragility curves are of varying robustness; see Sects. 4 and 5.3 for more details). The circle within each bar represents the median exceedance probability of each damage limit state; the length of each bar indicates the value of the corresponding standard deviation. Only intensity and PGA values with truncated exceedance probability ≥1 % for each damage limit state of each building type are plotted, since higher damage states can appear only for higher intensities or PGA values (see Sect. 5.2 for more details). Detailed values of median fragility and standard deviation are given in Table B1.
The median fragility curves derived from the discrete fragilities for empirical data and for analytical data are plotted in Figs. 7 and 8, respectively. To better illustrate the scatter of the originally collected discrete fragility data, the error analysis is attached with each regressed median fragility curve. As can be clearly seen from the regressed fragility curves in Figs. 7 and 8, there are two obvious trends: (1) for the same building type (masonry or RC), the higher the seismic resistance level (A < B), the lower the building fragility, which applies for all damage limit states; (2) for the same seismic resistance level, RC buildings have lower fragility than masonry buildings, which also applies for all damage limit states. These two trends indicate the reliability of the newly collected fragility database, the reasonability of the criteria in grouping building types and seismic resistance levels, and the suitability of using median fragility values to develop representative fragility curves for further analysis. However, some extra abnormality is also noteworthy; e.g., in the median fragility curve developed for LS4 of RC_B in Fig. 8, the probability of exceeding the LS4 damage limit state remains 0 even when PGA is higher than 0.8 g, which is obviously not the case in reality. Detailed sources of such abnormality and its effect on the intensity–PGA relation will be discussed in Sect. 5.3.
Table 4The median fragility curve parameters regressed from empirical and analytical fragility data. The three values in bold font indicate the low quality of the correspondingly regressed fragility curves (see Sect. 4 for more details).
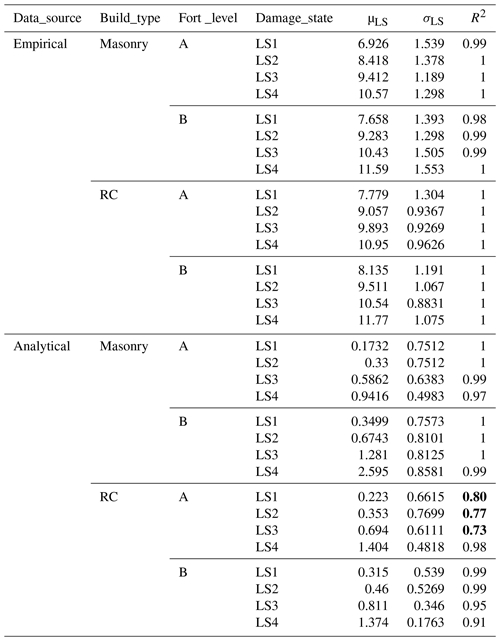
Note: “fort_level” A and B represent the pre-, low and moderate level and the high seismic resistance level, respectively; “damage_state” LS1, LS2, LS3 and LS4 represent the four damage limit states: slight, moderate, serious and collapse, respectively; “μLS” and “σLS” are the regression parameters between intensity or PGA and the corresponding fragilities of each damage limit state; R2 indicates the fitness quality of the regressed median fragility curve, as plotted in Figs. 7 and 8.
Mathematically, the goodness of fit of the consecutive median fragility curve from discrete median fragilities can be measured by statistical indicator R2 (Draper and Smith, 2014). A higher R2 value indicates a better fit of the regressed fragility curve, since it is defined as the ratio between SSR and SST : SSR is the sum of squares of the regression (), and SST is the total sum of squares (); yi refers to the original discrete fragilities for each damage limit state; refers to the mean fragility; refers to the predicted fragility by the fitted fragility curve. As shown in Table 4, the R2 values are generally above 0.95, which indicates the normal or lognormal distribution assumption in Eq. (3) is very suitable to match the discrete fragility datasets. Noticeably, there are also three low R2 values (≤0.8) in Table 4 for damage limit states LS1, LS2 and LS3 of building type RC_A, which may indicate the low quality (e.g., high scatter) of the originally collected fragility data. As can be cross validated from Fig. 4 and even better Figs. 6 and 8, the analytical fragility data for RC_A are more scattered than for other building types. This thus directly leads to the low R2 values in fitting the median fragility curve for damage limit states LS1, LS2 and LS3 of RC_A.
The intensity–PGA relation has an important application in seismic hazard assessment, since the use of macroseismic data can compensate for the lack of ground motion records and thus help in reconstructing the shaking distribution for historical events. Traditionally, intensity–PGA relations are developed using instrumental PGA records and macroseismic intensity observations within the same geographical range (Bilal and Askan, 2014; Caprio et al., 2015; Ding et al., 2014, 2017; Ding, 2016; Ogweno and Cramer, 2017; Worden et al., 2012). These relations are generally region-dependent and have large scatter (Caprio et al., 2015). In this section, we propose a new approach in deriving intensity–PGA relations based on the newly collected empirical and analytical fragility database. For each building type and each damage limit state, an empirical fragility curve (exceedance probability vs. macroseismic intensity) and an analytic fragility curve (exceedance probability vs. PGA) are available, as derived from the median fragilities in Sect. 4. By eliminating the same fragility value, we can derive the corresponding pair of macroseismic intensity and PGA. Thus, for a series of fragility values, we can further regress the corresponding intensity–PGA relation based on the paired intensities and PGAs. Ideally, we would expect the overlap of all these regressed intensity–PGA relations, regardless of the difference in building type, seismic resistance level and damage state.
5.1 Difference between this new approach and previous practices
Compared with this new approach in intensity–PGA relation development, previous practices directly regressed intensity and PGA datasets within the same geographical range, but no further classification of datasets, for example based on building type or damage state as in this study, was conducted. The lack of further classification of PGA and intensity datasets may explain why the previously derived intensity–PGA relations generally have high scatter. The reason is that, although macroseismic intensity is a direct macro indicator of building damage, higher instrumental ground motion (e.g., PGA) does not necessarily mean higher damage to all buildings. Instead, damage is more determined by the seismic resistance capacity of different building types. Thus, further division of intensity and instrumental ground motion records based on affected building types should promisingly help decrease the scatter of the regressed intensity–PGA relation.
Furthermore, the local site effect also contributes to the amplification of instrumental peak ground motions (PGA or SA), when combining intensity and PGA datasets from areas with different geological background together. This in turn increases the scatter of regressed intensity–PGA relation. In this regard, it is worth emphasizing that, in our PGA-related analytical fragility database, the PGA parameter is not the real instrumental records as used in regressing the traditional intensity–PGA relation, but rather the input PGA records used in experimental fragility analysis (pushover analysis, incremental dynamic analysis, dynamic history analysis, etc.). Therefore, the regional dependence (here we mainly refer to site condition), which contributes to the scatter of the traditional PGA–intensity relation, is not a source of uncertainty in our relation.
5.2 Derivation of initial intensity–PGA relation
As a tentative approach, here we derive the relation between intensity and PGA using median fragility as the bridge for each damage limit state of each building type. We are deeply aware that uncertainty is inherent in every single step in both empirical and analytical fragility analysis. However, the trial of using the median fragility as the bridge to develop the intensity–PGA relation proposed here, more importantly, aims at providing a new approach in this regard compared with traditional practice, not to reduce the uncertainties background (due to differences in building structure, seismic demand inputs, computation methods, etc.) in deriving empirical and analytical fragility. By using Eq. (3) for PGA–fragility and intensity–fragility, respectively, and eliminating fragility as a variable, we find
with
Here, the parameters μPGA, μInt, σPGA and σInt are taken from Table 4 with values varying across building types and damage limit states.
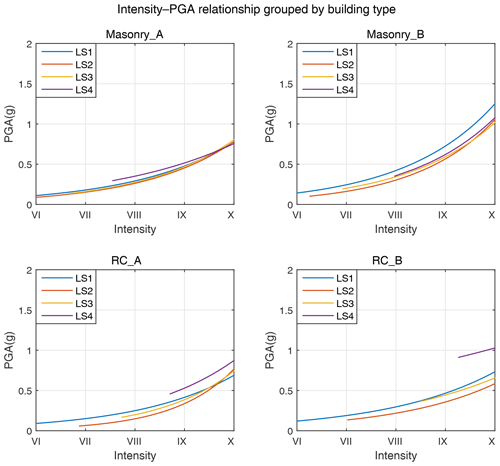
Figure 9Intensity–PGA relations grouped by building types. Only intensity and PGA values with truncated exceedance probability ≥1 % for each damage limit state of each building type are plotted, since higher damage states can appear only for higher intensities or PGA values (see Sect. 5.2 for more details).
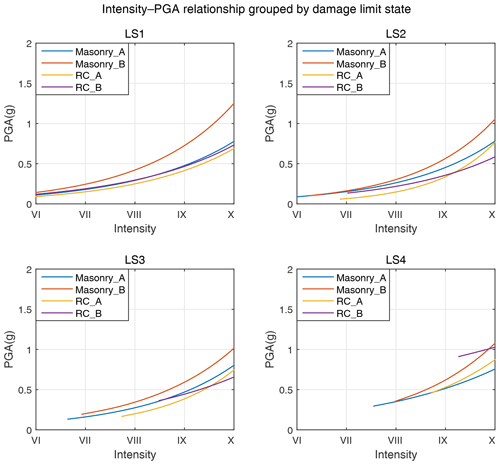
Figure 10Intensity–PGA relations grouped by damage limit states. Only intensity and PGA values with truncated exceedance probability ≥1 % for each damage limit state of each building type are plotted, since higher damage states can appear only for higher intensities or PGA values (see Sect. 5.2 for more details).
These intensity–PGA relations are plotted in Fig. 9 (grouped by building types) and Fig. 10 (grouped by damage limit states). Theoretically, higher damage states can occur only for higher intensities or PGA values. For instance, a LS4 damage state at intensity III would not happen, as reflected by the curves in Figs. 9 and 10: LS1 has the lowest PGA or intensity starting point, while LS4 has the highest. Thus, we plot the intensity–PGA curves for fragility values above 1 %. Ideally, we would expect the overlap of all relation curves between intensity and PGA, whether grouped by building type or by damage state. As a matter of fact, for building types Masonry_A and Masonry_B in Fig. 9, the four intensity–PGA curves of the four damage limit states coincide very well. Meanwhile, the discrepancy in intensity–PGA relations of RC_A for damage states LS1, LS2 and LS3 in Fig. 9 is not surprising, given the relatively high scatter in the original analytical fragility datasets of RC_A (as discussed in Sect. 4 and verified by Appendix Figs. A3–A4).
5.3 Source of abnormality in intensity–PGA curves
For building types RC_A and RC_B in Fig. 9, it is observed that for the same intensity levels, the corresponding PGA values of damage state LS4 are much higher than those of damage limit states LS1, LS2 and LS3. For a fixed fragility value, this may be due to the underestimation of intensity by the median empirical fragility curve in Fig. 7 or the overestimation of PGA by the median analytical fragility curve in Fig. 8 or a combination of both effects. In this regard, damage data scarcity at higher damage limit states may contribute to the abnormally high PGA values of LS4. When reviewing the fragility data collection process, it is clear that the construction of an empirical fragility database requires the combination of damage statistics from multiple earthquake events that cover a wide range of ground motion levels. Generally, large-magnitude earthquakes occur more infrequently in densely populated areas; thus damage data tend to cluster around the low damage states and ground motion levels. This limits the validation of high-damage states or ground motion levels (Calvi et al., 2006). According to Yuan (2008), those seriously damaged buildings in earthquake-affected areas are mainly masonry buildings. Therefore, the cause of the abnormally high PGA values of damage state LS4 for RC_A and RC_B can be attributed to the relative scarcity of damage data at higher intensity–PGA levels, especially for RC buildings.
As for the building types Masonry_A and Masonry_B in Fig. 9, for the same intensity level, the PGA values revealed by four damage states of Masonry_B are generally higher than those in Masonry_A. This can be more clearly seen from Fig. 10, in which the intensity–PGA relations are grouped by damage limit states and the PGA values revealed by Masonry_B are generally higher than by all the other building types. To better understand this abnormality, we need to refer to the building seismic resistance level assignment process in this study. In fact, compared with Masonry_A, buildings assigned as type Masonry_B generally have much higher seismic resistance capacity. As mentioned in Sect. 3.1, level A refers to buildings with pre-, low and moderate seismic resistance capacity, and level B refers to buildings with high seismic resistance capacity. According to the grouping criteria in Table 3, buildings assigned as Masonry_B mainly refer to those built after 2001 with seismic resistance level VIII and above. This is obviously a very high code standard (more building classification details can be found in the Supplement). Thus, for the same ground motion level, the damage posed on Masonry_B should be much slighter than on Masonry_A. Consequently, the corresponding intensity revealed by Masonry_B should be lower than by Masonry_A.
Currently in mainland China, the macroseismic intensity level in post-earthquake field surveys is determined by damage states of three reference buildings types, namely (1) Type A, wood structure, old soil, stone or brick building; (2) Type B, single-story or multistory brick masonry without seismic resistance; and (3) Type C, single-story or multistory brick masonry sustaining shaking of intensity degree VII. In this study, buildings assigned as Masonry_B mainly refer to those constructed after 2001 with seismic resistance level VIII and above, and their seismic resistance capability is obviously much higher than all three A–B–C building types. Therefore, intensity levels derived from damage to those less fragile Masonry_B buildings tend to be underdetermined. This may help explain why for the same intensity level the corresponding PGA revealed by the intensity–PGA relation of Masonry_B is higher than that of Masonry_A.
Based on the above discussion and the initial analysis in Sect. 4, it can be summarized that (a) due to the high scatter in the originally collected fragility database, the intensity–PGA relations derived for LS1, LS2 and LS3 of building type RC_A are of low robustness (as validated by the low R2 values in Table 4); (b) due to the damage data scarcity at high-damage states or ground motion levels, intensity–PGA relations for LS4 of RC_A and LS4 of RC_B are also not fully reliable; and (c) due to the high seismic resistance capability attached to Masonry_B, the intensity–PGA relations derived for all four damage limit states of Masonry_B have the probability of underestimating intensity (or overestimate PGA) compared with Masonry_A. Therefore, intensity–PGA curves derived for Masonry_A are of relatively highest robustness and reliability. Actually, the four intensity–PGA curves of Masonry_A do coincide very well as expected (Fig. 9). According to Yuan (2008), those seriously damaged buildings in earthquake-affected areas are also mainly masonry buildings. Therefore, we consider the median empirical and analytical fragility curves derived for Masonry_A (with uncertainties provided in Appendix Figs. A3–A4 and Table B1) to be the most representative ones for seismicity-prone areas in mainland China, compared with those developed for other building types in this study.
5.4 Average intensity–PGA relation derived for Masonry_A
According to the analysis in Sect. 5.3, intensity–PGA curves derived for the four damage limit states of Masonry_A are of the highest robustness. Therefore, we first focus only on building type Masonry_A and average its four curves for discrete intensity values, to derive the corresponding averaged PGA values, as listed in Table 5. If we match the data points in Table 5 with a linear relation between intensity and ln(PGA), we find Eq. (5):
where ε follows the normal distribution, with 0 as the median value and the standard deviation is σ.
Table 5The mean PGA values derived from intensity–PGA relations of Masonry_A based on the newly proposed approach (Sect. 5.4).
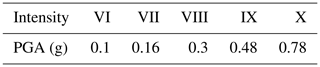
By integrating the uncertainty in both original empirical and analytical fragility data of Masonry_A (as shown in Appendix Figs. A3–A4 and Table B1) into the intensity–PGA relation, the averaged standard deviation σ in Eq. (5) is estimated to be 0.3 (the detailed uncertainty transmission methodology is given in Appendix C). As the Masonry_A type is the most common and relevant with buildings damaged in historical earthquakes (Yuan, 2008), we recommend using Eq. (5) for building damage assessment for earthquakes that occurred in mainland China, especially in seismic active provinces, e.g., Sichuan and Yunnan (Fig. 2).
5.5 Comparison with other intensity–PGA relations
Based on the summarization in Sect. 5.3, if we only remove those obviously unreliable intensity–PGA curves, namely LS1, LS2, LS3 and LS4 of RC_A and LS4 of RC_B, the range of median PGA values corresponding to each intensity degree can be derived from the remaining intensity–PGA relations, as shown in Table 6. For comparison, the recommended PGA range for each intensity degree in the Chinese Seismic Intensity Scale (GB/T 17742-2008, 2008) is listed in Table 7. The PGA values for intensities VI and VII in our results are higher than those in GB/T 17742-2008 (2008), while for intensities VII, IX and X, the PGA values are quite comparable. We also found that the recommended PGA ranges in GB/T 17742-2008 (2008) are indeed the same as those given in GB/T 17742-1980, which was issued in the 1980s around 4 decades ago. At that time, available damage information used to derive the intensity–PGA relation in China was quite scarce. Therefore, damaging earthquakes that occurred in the United States before 1971 were also largely used, which may not be representative of the situation in China today. Thus, one possible explanation for the relatively low PGAs for low intensity levels (VI, VII) in Table 7 (GB/T 17742-1980/2008) is that the buildings in the 1980s were more fragile than buildings today. Since macroseismic intensity is a direct macro indicator of building damage, today buildings generally have better seismic resistance capacity and thus require higher ground motion (PGA) than buildings in the 1980s to be equally damaged.
Since the recommended PGA ranges in GB/T 17742-2008 (2008) are not so representative of the current building status in mainland China, comparisons with the latest intensity–PGA relation developed in Ding et al. (2017) are also conducted. Ding et al. (2017) adopted the traditional practice in regressing the macroseismic intensities and instrumental PGA records within the same geographical range, by using records for 28 M≥5 earthquakes that occurred during 1994–2014 in mainland China. The PGA values for intensities VI–IX in Ding et al. (2017) are listed in Table 8. When comparing our results in Tables 5 and 6 with those in Table 8, PGA values are quite consistent for both low intensity (VI, VII) and high intensity (VIII, IX) levels, although these data are separately developed by our new approach and by traditional practice. This congruence shows the reasonability of our new approach proposed here in developing the intensity–PGA relation.
We established an empirical fragility database by evaluating 69 papers and theses, mostly from the Chinese literature, that document observations of macroseismic intensities reflecting earthquake damage that has occurred in densely populated areas in mainland China over the past 4 decades. These publications provide empirical fragilities dependent on macroseismic intensities for four damage limit states (LS1, LS2, LS3, LS4) of four building types (Masonry_A, Masonry_B, RC_A, RC_B). We also established an analytical fragility database by scrutinizing 18 papers and theses with results on modeling fragilities for the nominally same building types and the same damage states either by response spectral methods or by time-history response analysis. These analytic methods provide fragilities as functions of PGA. From this wealth of data, we derived the median fragility curves for these building types by removing outliers using the box-plot method.
We proposed a new approach by using fragility as the bridge and derived intensity–PGA relations independently for each building type and each damage state. The potential sources of abnormalities in these newly derived intensity–PGA relations were discussed in detail. Ideally the individual intensity–PGA curves should all coincide and allow us to derive an average relation between intensity and PGA. The coincidence is not 100 % perfect and deviations for the cases where they occur were discussed. Given the high-damage data abundance and wide distribution of masonry buildings in mainland China, for studies referring to historic earthquakes and their losses in seismic active regions, e.g., Sichuan and Yunnan, we recommend utilizing the intensity–PGA relation derived from Masonry_A buildings in Eq. (5).
However, for engineering applications, due to the scatter in original fragility datasets and the simplification in using median fragility to derive the intensity–PGA relation in our proposed new approach, the use of the preliminary intensity–PGA relations developed here should be with caution. It is also worth noting that buildings used for empirical intensity determination and for analytical studies do not coincide: a Masonry_A building in a post-event field survey may encompass a wider range than in an analytic study. Therefore, following the novel idea of using fragility as the bridge to develop an intensity–PGA relation in this study, possible extensions in the future can be performed with fragility analysis for more specifically designed building types that are more representative of those widely damaged building types in the field.
In Fig. A1, the comparison of the Chinese Seismic Intensity Scale with other internationally adopted scales is presented. Additionally, the correspondence relation between intensity and PGA–PGV range suggested by the current seismic intensity scale in China (GB/T 17742-2008, 2008) is also graphically presented in Fig. A2. To better illustrate the scatter of the original fragility datasets we collected, standard deviations of each fragility series are also plotted in Fig. A3 (empirical data) and Fig. A4 (analytical data).
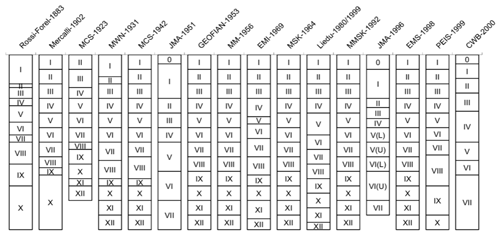
Figure A1Comparison of the Chinese Seismic Intensity Scale with other internationally used seismic scales (Daniell, 2014; after the work of Gorshkov and Shenkareva, 1960; Barosh, 1969; Musson et al., 2010). In this figure, “Liedu-1980/1999” represents the Chinese Seismic Intensity Scale, which has marginal change compared with the current intensity scale GB/T 17742-2008 (2008) used in China.
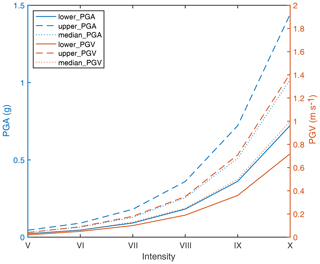
Figure A2The suggested correspondence relation between intensity and the PGA–PGV range by the Chinese Seismic Intensity Scale (GB/T 17742-2008, 2008).
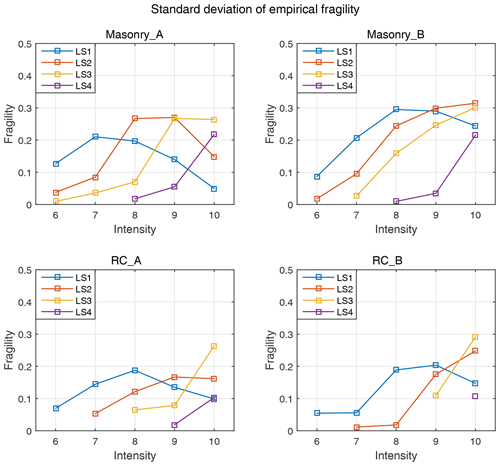
Figure A3Standard deviation of empirical fragility, namely the exceedance probability of each damage limit state (LS1, LS2, LS3, LS4) derived based on empirical fragility datasets for each building type (Masonry_A, Masonry_B, RC_A, RC_B; detailed values are given in Table B1). Only intensity and PGA values with truncated exceedance probability ≥1 % for each damage limit state of each building type are plotted, since higher damage states can appear only for higher intensities or PGA values (see Sect. 5.2 for more details).
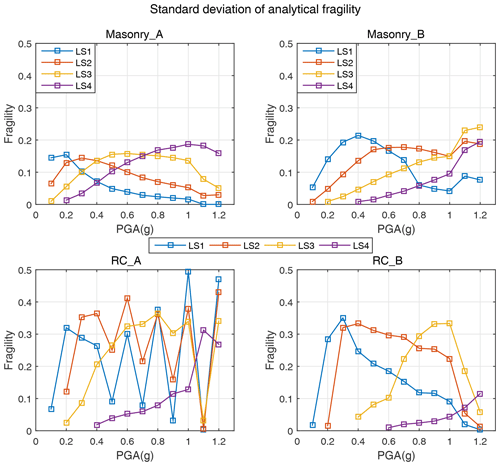
Figure A4Standard deviation of analytical fragility, namely the exceedance probability of each damage limit state (LS1, LS2, LS3, LS4) derived based on analytical fragility datasets for each building type (Masonry_A, Masonry_B, RC_A, RC_B; detailed values are given in Table B1). Only intensity and PGA values with truncated exceedance probability ≥1 % for each damage limit state of each building type are plotted, since higher damage states can appear only for higher intensities or PGA values (see Sect. 5.2 for more details).
In Table B1, more statistical details about our newly constructed fragility datasets, including the number of fragility data before and after removing the outliers, median fragility values used in deriving the fragility curve, and the standard deviation of each fragility dataset for each building type and each damage state in Figs. 7 and 8 are listed. Table B2 provides an unofficial English translation of China seismic intensity scale: GB/T 17742-2008 (2008), which is modified after CSIS (2019).
Table B1Statistics of fragility database for each damage limit state and each building type.
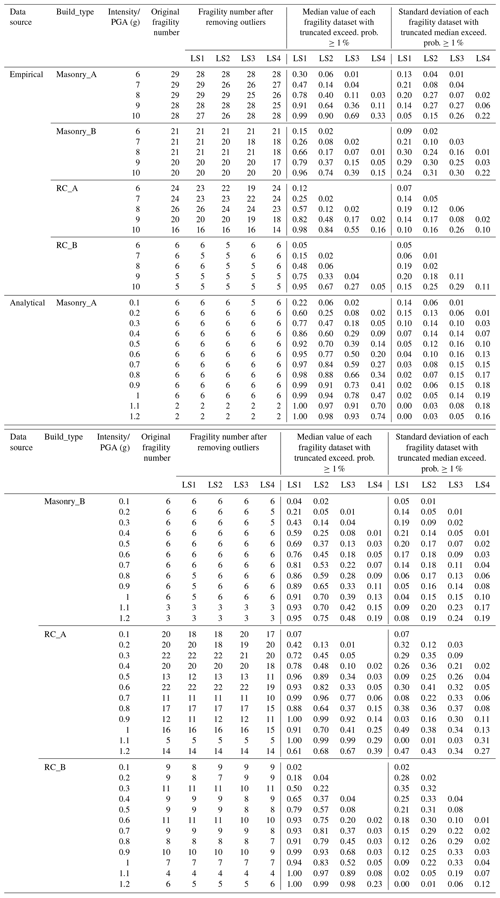
Note: “origin fragility number” refers to the number of original fragilities collected for each damage limit state of each building type from previous studies; “fragility number after removing outliers” refers to the remaining fragilities after removing outliers using the box-plot check method. Only intensity and PGA values with truncated exceedance probability ≥1 % for each damage limit state of each building type are given, since higher damage states can appear only for higher intensities or PGA values (see Sect. 5.2 for more details).
Table B2Official Chinese Seismic Intensity Scale: GB/T 17742-2008 (2008; modified after CSIS, 2019).
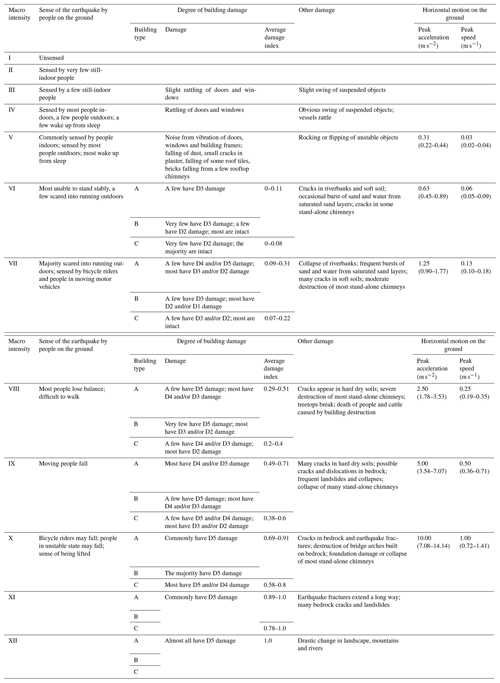
Notes about Qualifiers: very few: <10 %; few: 10 %–50 %; most: 50 %–70 %; majority: 70 %–90 %; commonly: >90 %.
The estimation of the uncertainty of the intensity–PGA relation (Eq. 5) is not a standard procedure like regression analysis. We have fragility as a function of intensity with an error on the fragility so that fragility is a random variable. It is also a random variable when derived as function of y=ln (PGA). We express this as
with i as intensity, y as ln(PGA) and f as fragility.
εg is a normally distributed random variable with zero mean, standard deviation σg.
εh is a normally distributed random variable with zero mean, standard deviation σh.
g(y) and h(i) are nonlinear functions that can be modeled as cumulative normal distributions in intensity and ln(PGA) as fragility ranges between 0 and 1. Under this condition, equating the expectation values of the fragilities
leads to a linear relation between ln(PGA) and intensity. Including uncertainties in this relation leads to the hypothesis
εy is a normally distributed random variable with zero mean, standard deviation σy, and this is the quantity we want to determine. Note that with this relation y becomes a random variable. Its expectation value is related to intensity via
We ask the following question. If the above relation holds and intensity is fixed, what range of values for y is possible so that
holds? Inserting the above expressions provides
If we assume that the error term is small, we can write
is the slope of the g(y) curve and has the unit 1∕ln (PGA). The value changes along the curve so that we replace it by an average value . Then,
and under the assumption of independence of the two random terms we get
In order to utilize this estimation scheme for our data, we approximate by its value at the 0.5 value of the fragility function: g(ym)=0.5, so that . When we do the estimates for each damage class and each building type, we find the standard deviations for ln(PGA) according to the following table. The values do vary, as listed in Table B3. A representative/average value appears to be 0.3.
More fragility extraction and building classification details are available in the Supplement: Supplementary_building_ classification_ details.pdf. The earthquake catalog in plotting Fig. 2 is in EQ_list_with_field_survey.xlsx. The empirical and analytical fragility data in Figs. 3 and 4 are available in data_Fig3-4.
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-20-643-2020-supplement.
JED proposed the idea to review the fragility literature for buildings in mainland China. DX conducted the review work and proposed the new approach in deriving intensity–PGA relation and wrote the manuscript. FW proposed the methodology of uncertainty transmission from the fragility to intensity–PGA relation. All authors contributed to the revision of the manuscript.
The authors declare that they have no conflict of interest.
The authors thank the Editor Maria Ana Baptista for actively monitoring the whole reviewing process. Furthermore, we thank the reviewer Mustafa Erdik and the other six anonymous reviewers for their constructively critical and helpful comments, which improved this manuscript substantially. We also acknowledge the thorough review of the language copy-editor and the typesetter of the journal NHESS, which has optimized the quality of our study greatly. Figure 2 was generated by the authors using Generic Mapping Tools (https://www.generic-mapping-tools.org/), which is also sincerely acknowledged.
This research has been supported by the China Scholarship Council (CSC) and by the Karlsruhe House of Young Scientists (KHYS) from the Karlsruhe Institute of Technology (KIT).
The article processing charges for this open-access
publication were covered by a Research
Centre of the Helmholtz Association.
This paper was edited by Maria Ana Baptista and reviewed by Mustafa Erdik and one anonymous referee.
A, N.: Simplified Prediction Methods of Earthquake Disaster Losses in Hohhot, MS Thesis, Inner Mongolia Normal University, Inner Mongolia, China, 45 pp., 2013 (in Chinese).
Antoniou, S. and Pinho, R.: Development and verification of a displacement-based adaptive pushover procedure, J. Earthq. Eng., 8, 643–661, https://doi.org/10.1080/13632460409350504, 2004.
Barosh, P. J.: Use of seismic intensity data to predict the effects of earthquakes and underground nuclear explosions in various geologic settings, U.S. Government Printing Office, Washington, D.C., USA, 1969.
Bie, D., Feng, Q., and Zhang, T.: A Research on Vulnerability of Brick-Concrete Buildings in Fujian Based on Partition of Region Characteristics, Journal of Catastrophe, 25, 254–257, https://doi.org/10.3969/j.issn.1000-811X.2010.z1.054, 2010 (in Chinese).
Bilal, M. and Askan, A.: Relationships between Felt Intensity and Recorded Ground-Motion Parameters for Turkey, B. Seismol. Soc. Am., 104, 484–496, https://doi.org/10.1785/0120130093, 2014.
Billah, A. H. M. M. and Alam, M. S.: Seismic fragility assessment of highway bridges: A state-of-the-art review, Struct. Infrastruct. E., 11, 804–832, https://doi.org/10.1080/15732479.2014.912243, 2015.
Calvi, G. M., Pinho, R., and Magenes, G.: Development of seismic vulnerability assessment methodologies over the past 30 years, ISET Journal of Earthquake Technology, 43, 75–104, available at: https://www.researchgate.net/publication/241826044 (last access: 24 February 2020), 2006.
Caprio, M., Tarigan, B., and Worden, C. B.: Ground motion to intensity conversion equations (GMICEs): A global relationship and evaluation of regional dependency, B. Seismol. Soc. Am., 105, 1476–1490, https://doi.org/10.1785/0120140286, 2015.
Chang, X., Alimujiang, Y., and Gao, C.: Disaster Loss Assessment and Characteristic of Seismic Hazard of Heshuo Earthquake with Ms5.0 in Xinjiang on Jan 8th, 2012, Inland Earthquake, 26, 279–285, https://doi.org/10.3969/j.issn.1001-8956.2012.03.012, 2012 (in Chinese).
Chen, H.: Study on Earthquake Damage Loss Assessment of Urban Buildings' Decorations, MS Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 108 pp., 2008 (in Chinese).
Chen, X., Sun, B., and Yan, P.: The characteristics of earthquake disasters distribution and seismic damage to structures in Kangding Ms 6.3 earthquake, Earthquake Engineering and Engineering Dynamics, 37, 1–9, https://doi.org/10.13197/j.eeev.2017.02.1.chenxz.001, 2017 (in Chinese).
Chen, Y., Chen, Q., and Chen, L.: Vulnerability Analysis in Earthquake Loss Estimate, Earthquake Research in China, 15, 97–105, 1999 (in Chinese).
GB/T 17742-2008: Chinese Seismic Intensity Scale, issued by General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China (AQSIQ) and Standardization Administration of the People's Republic of China (SAC), Beijing, China, 2008 (in Chinese).
CSIS: China seismic intensity scale, a non-official English translation based on contents in Wikipedia, available at: https://en.wikipedia.org/w/index.php?title=China_seismic_intensity_scale&oldid=812457225, last access: 21 May 2019.
Cui, Z. and Zhai, Y.: Research on Effects of Provincial Characteristic on Architecture, Journal of Catastrophe, 25, 271–274, 2010 (in Chinese).
Daniell, J.: Development of socio-economic fragility functions for use in worldwide rapid earthquake loss estimation procedures, PhD Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2014.
Del Gaudio, C., Ricci, P., and Verderame, G. M.: Development and urban-scale application of a simplified method for seismic fragility assessment of RC buildings, Eng. Struct., 91, 40–57, https://doi.org/10.1016/j.engstruct.2015.01.031, 2015.
Ding, B.: Study on Related Quantitative Parameters of Seismic Intensity Scale, PhD Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 195 pp., 2016 (in Chinese).
Ding, B., Sun, J., Li, X., Liu, Z., and Du, J.: Research progress and discussion of the correlation between seismic intensity and ground motion parameters, Earthq. Eng. Eng. Vib., 34, 7–20, https://doi.org/10.13197/j.eeev.2014.05.7.dingbr.002, 2014 (in Chinese).
Ding, B., Sun, J., and Du, K.: Study on relationships between seismic intensity and peak ground acceleration, peak ground velocity, Earthquake Engineering and Engineering Dynamics, 37, 26–36, https://doi.org/10.13197/j.eeev.2017.02.26.dingbr.004, 2017 (in Chinese).
Draper, N. R. and Smith, H: Applied Regression Analysis, 3rd edn., John Wiley & Sons, New York, USA, 2014.
Dumova-Jovanoska, E.: Fragility curves for reinforced concrete structures in Skopje (Macedonia) region, Soil Dyn. Earthq. Eng., 19, 455–466, https://doi.org/10.1016/S0267-7261(00)00017-8, 2000.
EMS1998: European Macro-seismic Scale 1998, European Seismological Commission, sub commission on Engineering Seismology, Working Group, Macro-seismic Scales, Conseil de l'Europe, Cahiers du Centre Européen de Géodynamique et de Séismologie, vol. 15, Luxembourg, 1998.
Fajfar, P.: A nonlinear analysis method for performance-based seismic design, Earthq. Spectra, 16, 573–592, https://doi.org/10.1193/1.1586128, 2000.
Fang, W., Wang, J., and Shi, P.: Comprehensive Risk Governance: Database, Risk Map and Web Platform, Science Press, Beijing, China, 2011 (in Chinese).
FEMA: Multi-hazard loss estimation methodology: earthquake model (HAZUS-MH-MR3), Technical Report, Washington, D.C., USA, available at: https://www.fema.gov/media-library/assets/documents/24609 (last access: 24 February 2020), 2003.
Freeman, S. A.: The capacity spectrum method, in: Proceedings of the 11th European Conference on Earthquake Engineering, 6–11 September 1998, Paris, France, available at: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.460.2405 (last access: 24 February 2020), 1998.
Freeman, S. A.: Review of the development of the capacity spectrum method, ISET Journal of Earthquake Technology, 41, 1–13, available at: https://engineering.purdue.edu/~ce573/Documents/SAF_Review of Capacity Spectrum Method.pdf (last access: 25 February 2020), 2004.
Gan, P.: Research on the Vulnerability and Damage Index of Seismic Building, MS Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 70 pp., 2009 (in Chinese).
Gao, H., Bie, D., and Ma, J.: A Research on Vulnerability for Brick-Residence Buildings in Wenchuan Earthquake Areas, World Earthquake Engineering, 26, 73–77, 2010 (in Chinese).
Ge, M., Chang, X., and Yiliyaer, A.: Direct Economic Loss and Post-earthquake Recovery and Reconstruction Fund Evaluation of Yutian Ms7.3 Earthquake on Feb.12, 2014, Inland Earthquake, 28, 104–112, https://doi.org/10.16256/j.issn.1001-8956.2014.02.003, 2014 (in Chinese).
Gorshkov, G. P. and Shenkareva, G. A.: On the Correlation of Seismic Scales, U.S. Joint Publications Research Service, New York, USA, available at: https://apps.dtic.mil/docs/citations/ADA362451 (last access: 25 February 2020), 1960.
Guo, X., Wang, Z., and Duan, C.: Earthquake Damage Assessment Method for Rural Timber Buildings, Building Science, 27, 64–67, https://doi.org/10.13614/j.cnki.11-1962/tu.2011.s2.035, 2011 (in Chinese).
Han, X., Wang, Y., and Zeng, J.: The Seismic Damage Assessment of M4.4 Earthquake of Yuncheng Saline Lake District in March 12, 2016, Shanxi Architecture, 43, 21–22, 2017 (in Chinese).
Hariri-Ardebili, M. A. and Saouma, V. E.: Seismic fragility analysis of concrete dams: A state-of-the-art review, Eng. Struct., 128, 374–399, https://doi.org/10.1016/j.engstruct.2016.09.034, 2016.
He, J. and Kang, R.: The Prediction of Seismic Hazard of Multi-Floor Brick Buildings in Weifang Area of Shandong Province, North China Earthquake Sciences, 17, 18–28, 1999 (in Chinese).
He, J., Pan, W., and Zhang, J.: Study on the Vulnerability of Buildings in Rural Areas of Yunnan Province Based on Seismic Damage Statistics Since 1993, Building Structure, 46, 379–383, 2016 (in Chinese).
He, P. and Fu, G.: Initial Research on Seismic Loss Prediction for Cities in Zhujiang Delta, South China Journal of Seismology, 29, 114–126, https://doi.org/10.13512/j.hndz.2009.04.015, 2009 (in Chinese).
He, S., Wang, Q., and Gong, P.: Seismic Damage Prediction of Rural Houses in Shiyan City, China Earthquake Engineering Journal, 39, 195–201, 2017 (in Chinese).
He, Y., Li, D., and Fan, K.: Research on the Seismic Vulnerabilities of Building Structure in Sichuan Region, Earthquake Research in China, 18, 52–58, https://doi.org/10.3969/j.issn.1001-4683.2002.01.005, 2002 (in Chinese).
Hu, S., Sun, B., and Wang, D.: Approach in Making Empirical Earthquake Damage Matrix, Earthq. Eng. Eng. Vib., 27, 46–50, https://doi.org/10.13197/j.eeev.2007.06.010, 2007 (in Chinese).
Hu, S., Sun, B., and Wang, D.: A Method for Earthquake Damage Prediction of Building Group Based on Building Vulnerability Classification, Earthq. Eng. Eng. Vib., 30, 96–101, https://doi.org/10.13197/j.eeev.2010.03.009, 2010 (in Chinese).
Hu, Y.: Earthquake Engineering, Seismological Press, Beijing, China, 1988 (in Chinese).
Li, J., Li, Y., and Zhou, R.: Characteristics of Surface Rupture and Building Damage by Ms 6.3 Earthquake in Kangding of Sichuan, China, Mountain Research, 33, 249–256, 2015 (in Chinese).
Li, P.: Research on Evaluation and Comparison of Seismic Performance in China's Rural Residential Buildings, MS Thesis, Ocean University of China, Qingdao, China, 106 pp., 2014 (in Chinese).
Li, S., Tan, M., and Wu, G.: Disaster Loss Assessment and Building Seismic Damage Characteristic of Atushi Earthquake with Ms5.2 in Xinjiang on March 11th, 2013, Inland Earthquake, 27, 341–347, https://doi.org/10.16256/j.issn.1001-8956.2013.04.007, 2013 (in Chinese).
Lin, S., Xie, L., and Gong, M.: Methodology for estimating seismic capacity of city building, Journal of Natural Disasters, 20, 31–37, https://doi.org/10.13577/j.jnd.2011.0405, 2011 (in Chinese).
Liu, H.: Seismic Disaster of Tangshan Earthquake, Seismological Press, Beijing, China, 1986 (in Chinese).
Liu, J.: Performance-based Seismic Design and Seismic Vulnerability Analysis for Isolated High-rise Buildings, MS Thesis, Guangzhou University, Guangzhou, China, 111 pp., 2014 (in Chinese).
Liu, J., Liu, Y., and Yan, Q.: Performance-based Seismic Fragility Analysis of CFST Frame Structures, China Civil Engineering Journal, 43, 39–47, https://doi.org/10.15951/j.tmgcxb.2010.02.017, 2010 (in Chinese).
Liu, Y.: Research on Vulnerability of RC Frame-core Wall Hybrid Structures Subjected to the Bidirectional Earthquake, MS Thesis, Xi'an University of Architecture and Technology, Xi'an, China, 80 pp., 2014 (in Chinese).
Liu, Z.: Study on Seismic Fragility of Tall Reinforced Concrete Structures, PhD Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 184 pp., 2017 (in Chinese).
Lv, G., Zhang, H., and Sun, L.: The Vulnerability Analysis of Important Buildings in Langfang City, Journal of Seismological Research, 40, 638–645, 2017 (in Chinese).
Ma, K. and Chang, Y.: Earthquake Disaster Prediction of Multistorey Masonry Building, Journal of Hefei University of Technology, 22, 58–61, 1999 (in Chinese).
Maio, R. and Tsionis, G.: Seismic fragility curves for the European building stock, JRC Technical Report, European Commission, Brussels, Belgium, https://doi.org/10.2788/586263, 2015.
Medvedev, S. and Sponheuer, W: Scale of seismic intensity (MSK1969), in: Proceedings of the 4th World Conference on Earthquake Engineering, Chilean Association of Seismology and Earthquake Engineering, 13–18 January 1969, Santiago, Chile, vol. 1, 143–153, available at: http://www.iitk.ac.in/nicee/wcee/article/4_vol1_A2-143.pdf (last access: 25 February 2020), 1969.
Meng, L., Zhou, L., and Liu, J.: Estimation of near-fault strong ground motion and intensity distribution of the 2014 Yutian, Xinjiang, Ms7.3 earthquake, Acta Seismologica Sinica, 36, 362–371, https://doi.org/10.3969/j.issn.0253-3782.2014.03.003, 2014 (in Chinese).
Meng, Z., Guo, M., and Zhao, H.: Seismic Damage Evaluation of the Important Multi-Storey Brick Concrete Buildings in Baoding, Technology for Earthquake Disaster Prevention, 7, 397–403, https://doi.org/10.3969/j.issn.1673-5722.2012.04.008, 2012 (in Chinese).
Meng, Z., Zhao, H., and Guo, M.: Research on Seismic Damage Prediction of the Building Complex in Baoding, Journal of Seismological Research, 36, 202–206, https://doi.org/10.3969/j.issn.1000-0666.2013.02.011, 2013 (in Chinese).
Ming, X., Zhou, Y., and Lu, Y.: Evaluation of Building Features and Seismic Capacity in Northwest Yunnan, Journal of Seismological Research, 40, 646–654, https://doi.org/10.3969/j.issn.1000-0666.2017.04.017, 2017 (in Chinese).
Musson, R. M., Grünthal, G., and Stucchi, M.: The comparison of macroseismic intensity scales, J. Seismol., 14, 413–428, 2010.
Nakamura, H.: Preliminary report on the great Hanshin Earthquake January 17, 1995 (AIJ1995), Japan Society of Civil Engineers, Tokyo, Japan, available at: http://resolver.tudelft.nl/uuid:96f94279-326a-483c-ac1d-c7f9e9226342 (last access: 25 February 2020), 1995.
Ogweno, L. P. and Cramer, C. H.: Improved CENA regression relationships between Modified Mercalli Intensities and ground motion parameters, B. Seismol. Soc. Am., 107, 180–197, https://doi.org/10.1785/0120160033, 2017.
Piao, Y.: Study on Housing Seismic Vulnerability of Yunnan and Qinghai Province, MS Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 72 pp., 2013 (in Chinese).
Qiu, S. and Gao, H.: The Research of Rural Dwelling's Seismic Vulnerability in Qinghai, Technology for Earthquake Disaster Prevention, 10, 969–978, https://doi.org/10.11899/zzfy20150415, 2015 (in Chinese).
Rossetto, T. and Elnashai, A.: Derivation of vulnerability functions for European-type RC structures based on observational data, Eng. Struct., 25, 1241–1263, https://doi.org/10.1016/S0141-0296(03)00060-9, 2003.
Rota, M., Penna, A., and Magenes, G.: A methodology for deriving analytical fragility curves for masonry buildings based on stochastic nonlinear analyses, Eng. Struct., 32, 1312–1323, https://doi.org/10.1016/j.engstruct.2010.01.009, 2010.
Shi, W., Chen, K., and Li, S.: Hazard Index and Intensity of the 2007 Ning'er, Yunnan, Ms6.4 Earthquake, Journal of Seismological Research, 30, 379–383, https://doi.org/10.3969/j.issn.1000-0666.2007.04.012, 2007 (in Chinese).
Shi, Y., Gao, X., and Tan, M.: Disaster Loss Assessment of the Minxian-Zhangxian Ms6.6 Earthquake, 2013, China Earthquake Engineering Journal, 35, 717–723, https://doi.org/10.3969/j.issn.1000-0844.2013.04.0717, 2013 (in Chinese).
Song, L., Tang, L., and Yin, L.: Method for Establishing Fragility Matrix of Groups of Buildings in Shihezi City and its Earthquake Disaster Prediction, Inland Earthquake, 15, 320–325, https://doi.org/10.3969/j.issn.1001-8956.2001.04.005, 2001 (in Chinese).
Sun, B. and Chen, H.: Urban Building Loss Assessment Method Considering the Decoration Damage due to Earthquake, Earthq. Eng. Eng. Vib., 29, 164–169, 2009 (in Chinese).
Sun, B. and Zhang, G.: Statistical Analysis of the Seismic Vulnerability of Various Types of Building Structures in Wenchuan M8.0 Earthquake, China Civil Engineering Journal, 45, 26–30, https://doi.org/10.15951/j.tmgcxb.2012.05.015, 2012 (in Chinese).
Sun, B., Wang, M., and Yan, P.: Damage Characteristics and Seismic Analysis of Single-storey Brick Bent Frame Column Industrial in Lushan Ms7.0 Earthquake, Earthq. Eng. Eng. Vib, 33, 1–8, 2013 (in Chinese).
Sun, B., Chen, H., and Yan, P.: Research on Zoned Characteristics of Buildings Seismic Capacity along North South Seismic Belt-take Sichuan Province as an Example, China Civil Engineering Journal, 47, 6–10, https://doi.org/10.15951/j.tmgcxb.2014.s1.002, 2014 (in Chinese).
Sun, L.: Research on the Earthquake Disaster Loss Assessment Method for Urban Areas and System Development, PhD Thesis, Xi'an University of Architecture and Technology, Xi'an, China, 171 pp., 2016 (in Chinese).
Vamvatsikos, D. and Cornell, C. A.: Incremental dynamic analysis, Earthquake Engineering and Structural Dynamics, 31, 491–514, https://doi.org/10.1002/eqe.141, 2002.
Vamvatsikos, D. and Fragiadakis, M.: Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty, Earthquake Engineering and Structural Dynamics, 39, 141–163, https://doi.org/10.1002/eqe.935, 2010.
Wang, D. L., Wang, X. Q., and Dou, A. X.: Primary study on the quantitative relationship between the typical building structures in western China, Earthquake, 27, 105–110, https://doi.org/10.3969/j.issn.1000-3274.2007.03.014, 2007 (in Chinese).
Wang, G.: The Performance-based Fragility Analysis of Base-isolated RC Frame Structure, MS Thesis, Lanzhou University of Technology, Lanzhou, China, 75 pp., 2013 (in Chinese).
Wang, H., Huang, H., and Yu, W.: Analysis on the Regional Building Vulnerability Based on the Damage Influencing Factors, Inland Earthquake, 25, 275–282, https://doi.org/10.16256/j.issn.1001-8956.2011.03.001, 2011 (in Chinese).
Wang, Y.: The Research and Manufacture of Urban Buildings Seismic Disasters Prediction Information System Based on ArcGIS, MS Thesis, Jiangxi University of Science and Technology, Ganzhou, China, 99 pp., 2007 (in Chinese).
Wang, Y., Shi, P., and Wang, J.: The Housing Loss Assessment of Rural Villages Caused by Earthquake Disaster in Yunnan Province, Acta Seismologica Sinica, 27, 551–560, https://doi.org/10.3321/j.issn:0253-3782.2005.05.010, 2005 (in Chinese).
Wei, F., Cai, Z., and Jiao, S.: A Fast Approach to Regional Hazard Evaluation Based on Population Statistical Data, Acta Seismologica Sinica, 30, 518–524, https://doi.org/10.3321/j.issn:0253-3782.2008.05.010, 2008 (in Chinese).
Wen, H., Hu, W., and Tan, M.: Preliminary Analysis on Earthquake Disaster of Building in Two Destructive Earthquakes of Xinjiang, Inland Earthquake, 31, 325–334, https://doi.org/10.16256/j.issn.1001-8956.2017.04.001, 2017 (in Chinese).
Wenliuhan, H., Zhang, Y., and Wang, D.: Review on Seismic Vulnerability and Economic Loss Assessment of Engineering Structures, Journal of Architecture and Civil Engineering, 32, 17–29, https://doi.org/10.3969/j.issn.1673-2049.2015.06.003, 2015 (in Chinese).
Worden, C. B., Gerstenberger, M. C., and Rhoades, D. A.: Probabilistic relationships between Ground-Motion parameters and modified Mercalli intensity in California, B. Seismol. Soc. Am., 102, 204–221, https://doi.org/10.1785/0120110156, 2012.
Wu, S.: Seismic Vulnerability Analysis of Masonry Buildings, MS Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 85 pp., 2015 (in Chinese).
Xia, S.: Assessment of Seismic Intensity with Mean Damage Index in an Earthquake-resistant Region, MS Thesis, Institute of Geophysics, China Earthquake Administration, Beijing, China, 128 pp., 2009 (in Chinese).
Xu, W. and Gao, M.: Statistical analysis of the completeness of earthquake catalogues in China mainland, China Journal of Geophysics, 57, 2802–2281, https://doi.org/10.6038/cjg20140907, 2014 (in Chinese).
Yang, G.: The study of vulnerability analysis of existing buildings under earthquake disaster, MS Thesis, Shenyang Jianzhu University, Shenyang, China., 78 pp., 2015 (in Chinese).
Yang, X.: Rapid Loss Assessment for Earthquake Disaster Using Seismic Spatial Information Grid, PhD, Thesis, Huazhong University of Science and Technology, Wuhan, China, 121 pp., 2014 (in Chinese).
Yang, X., Yang, J., and Che, W.: Seismic Vulnerability Study of Buildings in Different Enforcing Zones in Yunnan Province, Value Engineering, 12, 229–232, https://doi.org/10.14018/j.cnki.cn13-1085/n.2017.12.095, 2017 (in Chinese).
Ye, Z., Yan, J., and Yang, L.: Study on the Earthquake Damage Characteristics of Tibetan Dwellings in Sichuan Province, Earthquake Research in Sichuan, 4, 24–29, https://doi.org/10.13716/j.cnki.1001-8115.2017.04.007, 2017 (in Chinese).
Yin, Z.: Classification of Structure Vulnerability and Evaluating Earthquake Damage from Future Earthquake, Earthquake Research in China, 12, 49–55, 1996 (in Chinese).
Yin, Z., Li, S., and Yang, S.: Estimating Method of Seismic Damage and Seismic Loss, Earthq. Eng. Eng. Vib., 10, 99–108, https://doi.org/10.13197/j.eeev.1990.01.010, 1990 (in Chinese).
Yu, X., Lv, D., and Fan, F.: Seismic Damage Assessment of RC frame Structures Based on Vulnerability Index, Engineering Mechanics, 34, 69–75, https://doi.org/10.6052/j.issn.1000-4750.2015.09.0731, 2017 (in Chinese).
Yuan, Y.: Impact of intensity and loss assessment following the great Wenchuan Earthquake, Earthq. Eng. Eng. Vib., 7, 247–254, https://doi.org/10.1007/s11803-008-0893-9, 2008.
Zeng, Z.: Fragility Analysis and Seismic Reliability of the Isolated Structure, MS Thesis, Guangzhou University, Guangzhou, China, 110 pp., 2012 (in Chinese).
Zhang, G. and Sun, B.: A Method for Earthquake Damage Prediction of Building Groups Based on Multiple Factors, World Earthquake Engineering, 26, 26–30, 2010 (in Chinese).
Zhang, J., Pan, W., and Song, Z.: An Assessment of Seismic Vulnerability of Urban Structures Based on the Intensity Gap, Earthquake Engineering and Engineering Dynamics, 37, 77–84, https://doi.org/10.13197/j.eeev.2017.04.77.zhangj.009, 2017 (in Chinese).
Zhang, Q., Cheng, M., and Niu, L.: Seismic Vulnerability Analysis of Masonry Structures after Earthquake in Panzhihua Area, Architecture Application, 10, 110–112, https://doi.org/10.16001/j.cnki.1001-6945.2016.10.023, 2016 (in Chinese).
Zhang, T., Gao, H., and Huang, H.: Study on Regional Factors that Influence the Results of Vulnerability Analysis – A Case Study in Fujian, Journal of Catastrophe, 26, 73–77, https://doi.org/10.3969/j.issn.1000-811X.2011.03.015, 2011 (in Chinese).
Zhang, Y., Kang, J., and Wei, M.: Seismic Damage Evaluation of Building Based on GIS in Changchun, Journal of Northeast Normal University, 46, 124–131, 2014 (in Chinese).
Zheng, S., Yang, W., and Yang, F.: Seismic Fragility Analysis for RC Core Walls Structure Based on MIDA Method, Journal of Vibration and Shock, 34, 117–123, https://doi.org/10.13465/j.cnki.jvs.2015.01.021, 2015 (in Chinese).
Zhou, G., Tan, W., and Shi, W.: Seismic Hazard Matrix of House Construction in Yunnan, Earthquake Research in China, 23, 115–123, https://doi.org/10.3969/j.issn.1001-4683.2007.02.001, 2007 (in Chinese).
Zhou, G., Fei, M., and Xie, Y.: Discussion of the Intensity VIII of the Ms5.8 Yingjiang Earthquake on Mar. 10, 2011, Journal of Seismological Research, 34, 207–213, https://doi.org/10.3969/j.issn.1000-0666.2011.02.017, 2011 (in Chinese).
Zhou, G., Hong, L., and Liu, C.: Research on Assessment of Building Direct Economic Loss of Earthquake Based on GIS, Geomatics and Spatial Information Technology, 36, 56–59, https://doi.org/10.3969/j.issn.1672-5867.2013.10.017, 2013 (in Chinese).
Zhou, W. and Wang, S.: Investigation and Vulnerability Analysis of the Dwellings in South Fujian Province, Journal of Fuzhou University, 43, 123–128, https://doi.org/10.7631/issn.1000-2243.2015.01.0123, 2015 (in Chinese).
Zhu, J.: Seismic Fragility and Risk Analysis of RC Buildings, PhD Thesis, Xi'an University of Architecture and Technology, Xi'an, China, 153 pp., 2010 (in Chinese).
- Abstract
- Introduction
- Review of building fragility studies in mainland China
- Fragility database analysis
- Derivation of representative fragility curves
- New approach in deriving intensity–PGA relation
- Conclusion
- Appendix A
- Appendix B
- Appendix C: Methodology in characterization of uncertainty transmission from empirical and analytical fragility database to intensity–PGA relation
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Article
(5840 KB) - Full-text XML
- Abstract
- Introduction
- Review of building fragility studies in mainland China
- Fragility database analysis
- Derivation of representative fragility curves
- New approach in deriving intensity–PGA relation
- Conclusion
- Appendix A
- Appendix B
- Appendix C: Methodology in characterization of uncertainty transmission from empirical and analytical fragility database to intensity–PGA relation
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement