the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Ensemble flood simulation for a small dam catchment in Japan using nonhydrostatic model rainfalls – Part 2: Flood forecasting using 1600-member 4D-EnVar-predicted rainfalls
Kenichiro Kobayashi
Le Duc
Apip
Tsutao Oizumi
Kazuo Saito
This paper is a continuation of the authors' previous paper (Part 1) on the feasibility of ensemble flood forecasting for a small dam catchment (Kasahori dam; approx. 70 km2) in Niigata, Japan, using a distributed rainfall–runoff model and rainfall ensemble forecasts. The ensemble forecasts were given by an advanced four-dimensional, variational-ensemble assimilation system using the Japan Meteorological Agency nonhydrostatic model (4D-EnVar-NHM). A noteworthy feature of this system was the use of a very large number of ensemble members (1600), which yielded a significant improvement in the rainfall forecast compared to Part 1. The ensemble flood forecasting using the 1600 rainfalls succeeded in indicating the necessity of emergency flood operation with the occurrence probability and enough lead time (e.g., 12 h) with regard to an extreme event. A new method for dynamical selection of the best ensemble member based on the Bayesian reasoning with different evaluation periods is proposed. As the result, it is recognized that the selection based on Nash–Sutcliffe efficiency (NSE) does not provide an exact discharge forecast with several hours lead time, but it can provide some trend in the near future.
- Article
(6212 KB) - Companion paper
- BibTeX
- EndNote
Flood simulation driven by ensemble rainfalls has attracted more attention in recent years, resulting in a lot of useful information that ensemble flood forecasts can provide in flood control, such as forecast uncertainty, probabilities of rare events and potential flooding scenarios. In the Japanese case, it is considered that the ensemble rainfall simulation with a high resolution (2 km or below) is desirable, since extreme rainfall often takes place due to mesoscale convective systems and the river catchments are not as large as continental rivers; even the largest Tone River basin is around 17 000 km2.
A good review of ensemble flood forecasting using medium-term global and European ensemble weather forecasts (2–15 d ahead) by numerical weather prediction (NWP) models can be found in Cloke and Pappenberger (2009). In much of their review, the resolution of NWP model is relatively coarse (over 10 km), the number of ensembles is moderate (10–50) and the target catchment size is often large (e.g., Danube River Basin). They basically reviewed global and European ensemble prediction systems (EPSs) but also introduced some research on regional EPSs nested into global EPSs (e.g., Marsigli et al., 2001). They stated that “One of the biggest challenges therefore in improving weather forecasts remain to increase the resolution and identify the adequate physical representations on the respective scale, but this is a source hungry task”.
Short-term flood forecasting (1–3 d) based on ensemble NWPs is gaining more attention in Japan. Kobayashi et al. (2016) dealt with an ensemble flood (rainfall–runoff) simulation of a heavy-rainfall event that occurred in 2011 over a small dam catchment (Kasahori dam; approx. 70 km2) in Niigata, central Japan, using a rainfall–runoff model with a resolution of 250 m. Eleven-member ensemble rainfalls by the Japan Meteorological Agency nonhydrostatic model (JMA-NHM; Saito et al., 2006) with horizontal resolutions of 2 and 10 km were employed. The results showed that, although the 2 km EPS reproduced the observed rainfall much better than the 10 km EPS, the resultant cumulative and hourly maximum rainfalls still underestimated the observed rainfall. Thus, the ensemble flood simulations with the 2 km rainfalls were still not sufficiently valid, and a positional lag correction of the rainfall fields was applied. Using this translation method, the magnitude of the ensemble rainfalls and likewise the inflows to the Kasahori dam became comparable with the observed inflows.
Other applications of the 2 km EPS, which permit deep convection on some level, can be found in studies, for example that of Xuan et al. (2009). They carried out an ensemble flood forecasting at the Brue catchment, with an area of 135 km2, in southwestern England, UK. The resolution of their grid-based distributed rainfall–runoff model (GBDM) was 500 m, and the resolution of their NWP forecast by the PSU/NCAR (Pennsylvania State University–National Center for Atmospheric Research) mesoscale model (MM5) was 2 km. The NWP forecast was the result of downscaling of the global forecast datasets from the European Centre for Medium-Range Weather Forecasts (ECMWF). Fifty members of the ECMWF EPS and one deterministic forecast were downscaled. Since the original NWP rainfall of a grid average still underestimates the intensity compared with rain gauges, they introduced a best-match approach (location correction) and a bias-correction approach (scale-up) on the downscaled rainfall field. The results showed that the ensemble flood forecasting of some rainfall events is in good agreement with observations within the confidence intervals, while that of other rainfall events failed to capture the basic flow patterns.
Likewise in Europe, Hohenegger et al. (2008) carried out the cloud-resolving ensemble weather simulations of the August 2005 Alpine flood. Their cloud-resolving EPS of 2.2 km grid space included the explicit treatment of deep convection and was the result of downscaling of COSMO-LEPS (10 km resolution driven by ECMWF EPS). Their conclusion was that despite the overall small differences, the 2.2 km cloud-resolving ensemble produces results as good as and even better than its 10 km EPS, though the paper did not deal with the hydrological forecasting. Another paper which dealt with cloud-resolving ensemble simulations can be found in Vie et al. (2011) for a Mediterranean heavy-precipitation event. Their ensemble weather simulation model resolution was 2.5 km by AROME from Météo-France, which uses ALADIN forecasts for lateral boundary conditions (10 km resolution); thus the deep convection was explicitly resolved. We can recognize from this research that the European researchers especially around mountain regions have been farsighted from early days for the importance of these cloud-resolving ensemble simulations.
On the other hand, in Japan, Yu et al. (2018) have also used a post-processing method using the spatial shift of NWP rainfall fields for correcting the misplaced rain distribution. Their study areas are the Futatsuno (356.1 km2) and Nanairo (182.1 km2) dam catchments of the Shingu river basin, located on the Kii Peninsula, Japan. The resolutions of the ensemble weather simulations were 10 and 2 km by JMA-NHM, which is similar to the downscaling EPS in Kobayashi et al. (2016) but for a different heavy-rainfall event in western central Japan caused by a typhoon. The results showed that the ensemble forecasts produced better results than the deterministic control run forecast, although the peak discharge was underestimated. Thus, they also carried out a spatial shift of the ensemble rainfall field. The results showed that the flood forecasting with the spatial shift of the ensemble rainfall members was better than the original one; likewise the peak discharges more closely approached the observations.
Recently, as a further improvement upon the 2 km downscale ensemble rainfall simulations used by Kobayashi et al. (2016), Duc and Saito (2017) developed an advanced data assimilation system with the ensemble variational method (EnVar) and increased the number of ensemble members to 1600. This new data assimilation system was aimed to improve the rainfall forecasts of the 2011 Niigata–Fukushima heavy-rainfall event (JMA, 2013; Niigata Prefecture, 2011). The torrential rain of this event occurred over the small area along the synoptic-scale stationary front (for surface weather map, see Fig. 1 of Kobayashi et al., 2016). Saito et al. (2013) found that the location where intense rain concentrates varied in small changes of the model setting; thus the position of the heavy rain was likely controlled by horizontal convergence along the front rather than the orographic forcing.
Since the new EPS produced better forecasts of the rainfall fields, in this study, Part 2 of Kobayashi et al. (2016), we applied those 1600-member ensemble rainfalls to the ensemble inflow simulations of Kasahori dam. In this series, consisting of Part 1 and 2, we intentionally chose a rainfall–runoff model whose specification is quite close to those runoff models used in many governmental practices of Japanese flood forecasting to see the usefulness of 1600-member ensemble rainfalls. Our objective is to assess impact of the improvement of the rainfall forecast over the large area around Kasahori dam on the streamflow forecast for the Kasahori dam. In Part 1 the technique of positional lag correction was applied to match the rainfall forecasts with the observations to have a better hydrological forecast. This technique is hard to apply in real-time flood forecasting, since rainfall observations are unknown and there are a lot of potential positional lag vectors to choose from. Statistically the positional lag vector should respond to the local orographic features, but it may vary depending on the synoptic condition on the day and model forecast errors in a specific event. Thus the positional lag vector for one extreme rainfall event basically cannot be applied to other extreme event as is. The new EPS is expected to remove the use of such a technique.
In addition, the very large number of ensemble members, which is 10 to 20 times larger than the typical number of ensemble members currently run in operational forecast centers, poses new issues needed to solve in computation and interpretation. First, regional forecast centers may not afford running 1600 hydrological forecasts in real time, and a method to choose the most important members may be helpful. Such a method is known as ensemble reduction in ensemble forecasts (Molteni et al., 2001; Montani et al., 2011; Hacker et al., 2011; Weidle et al., 2013; Serafin et al., 2019), which is built upon cluster analysis when observations are not used as guidance for selection. However, our problem is more interesting when we can access the observations in the first few hours, and ensemble reduction should make use of these past observations in selecting important members. Second, it is more challenging to interpret the result when temporal and spatial uncertainties are realized to be more distinct now. Without taking such uncertainties into account, the ensemble forecasts are easily to be considered useless.
The organization of this paper is as follows. Section 2 describes the new mesoscale EPS and its forecast and rainfall verification results. Section 3 describes the rainfall–runoff model for explaining the changes in the model parameters. Results are shown in Sect. 4. In Sect. 5, concluding remarks and future aspects are presented.
2.1 Ensemble prediction system
An advanced mesoscale EPS was developed and employed to prepare precipitation data for the rainfall–runoff model. The EPS was built around the operational mesoscale model JMA-NHM for its atmospheric model as the downscale EPS conducted by Saito et al. (2013). In this study, a domain consisting of 819×715 horizontal grid points and 60 vertical levels was used for all ensemble members. This domain had a grid spacing of 2 km and covered the mainland of Japan. With this high resolution, convective parameterization was switched off. Boundary conditions were obtained from forecasts of the JMA's global model. Boundary perturbations were interpolated from forecast perturbations of the JMA's operational 1-week EPS as in Saito et al. (2013).
To provide initial conditions and initial perturbations for the EPS, a four-dimensional, variational-ensemble assimilation system using the Japan Meteorological Agency nonhydrostatic model (4D-EnVar-NHM) was newly developed in which background error covariances were estimated from short-range ensemble forecasts by JMA-NHM before being plugged into functions for minimization to obtain the analyses (Duc and Saito, 2017). If the number of ensemble members is limited, ensemble error covariances contain sampling noises which manifest as spurious correlations between distant grid points. In data assimilation, the so-called localization technique is usually applied to remove such noise, but at the same time it removes significant correlations in error covariances. In this study, we chose 1600 members in running the ensemble part of 4D-EnVar-NHM to retain significant vertical correlations, which have a large impact on heavy-rainfall events like the Niigata–Fukushima heavy rainfall. That means only horizontal localization is applied in 4D-EnVar-NHM. The horizontal localization length scales were derived from the climatologically horizontal correlation length scales of the JMA's operational four-dimensional, variational assimilation system JNoVA by dilation using a factor of 2.0.
Another special aspect of 4D-EnVar-NHM is that a separate ensemble Kalman filter was not needed to produce the analysis ensemble. Instead, a cost function was derived for each analysis perturbation, and minimization was then applied to obtain this perturbation, which is very similar to the case of analyses. This helped to ensure consistency between analyses and analysis perturbations in 4D-EnVar-NHM when the same background error covariance, the same localization and the same observations were used in both cases. To accelerate the running time, all analysis perturbations were calculated simultaneously using the block algorithm to solve the linear equations with multiple right-hand-side vectors resulting from all minimization problems. The assimilation system was started at 09:00 JST on 24 July 2011 with a 3 h assimilation cycle. All routine observations at the JMA's database were assimilated into 4D-EnVar-NHM. The assimilation domain was the same as the former operational system at the JMA. To reduce the computational cost, a dual-resolution approach was adopted in 4D-EnVar-NHM where analyses had a grid spacing of 5 km, whereas analysis perturbations had a grid spacing of 15 km. The analysis and analysis perturbations were interpolated to the grid of the ensemble prediction system to make the initial conditions for deterministic and ensemble forecasts.
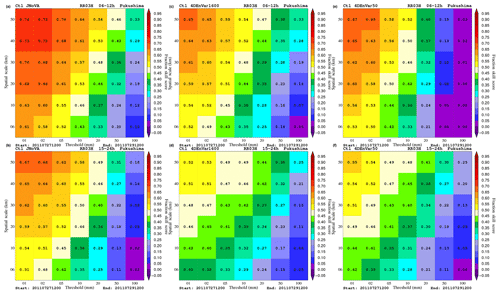
Figure 1Fraction skill scores of 3 h precipitation at Niigata–Fukushima from deterministic forecasts initialized by analyses from JNoVA (a, b) and 4D-EnVar-NHM using 1600 (c, d) and 50 members (e, f). These scores are averaged over the period from 21:00 JST on 24 July to 21:00 JST on 29 July 2011. To obtain robust statistics, precipitation is aggregated over the first 12 h forecasts (valid between 3 and 12 h forecast) and the next 12 h forecasts (valid between 12 and 24 h forecasts) as shown in the top and bottom rows, respectively. Note that the first 3 h precipitation is discarded due to the spin-up problem.
2.2 Rainfall verification
Due to limited computational resources, ensemble forecasts with 1600 members were only employed for the target time of 00:00 JST on 29 July 2011. However, deterministic forecasts were run for all other initial times to examine the impact of the number of ensemble members on analyses and the resulting forecasts. Figure 1 shows the verification results for the 3 h precipitation forecasts as measured by the fraction skill score (FSS; Roberts and Lean, 2008). Given a rainfall threshold and an area around a grid point, which is called a neighborhood, the FSS measures the relative difference between observed and forecasted rainfall fractions in this area. This verification score is used to mitigate difficulty in rainfall verification at the grid scale with very high resolution forecasts in which high variability in rain fields usually makes the traditional scores inadequate due to their requirement of an exact match between observations and forecasts at grid points. Thus the solution that the FSS follows is to consider forecast quality at spatial scales coarser than the grid scale by comparing forecasts and observations not at grid points but at neighborhoods whose sizes are identified with spatial scales. The FSS is normalized to range from 0 to 1, with the value of 1 indicating a perfect forecast and the value of 0 being a no-skill forecast which can be obtained by a random forecast.
In Fig. 1 we aggregate the 3 h precipitation in the first and second 12 h forecasts to increase samples in calculating the FSS. In this way, robust statistics are obtained, but at the same time dependence of the FSS on the leading times can still be shown. Note that an additional experiment with 4D-EnVar-NHM using 50 ensemble members, which is called 4DEnVar50 to differentiate it from the original one, 4DEnVar1600, was run. The main difference between 4DEnVar50 and 4DEnVar1600 is that vertical localization was applied in the former case to generate its ensemble members. As mentioned in the previous section, vertical localization can potentially weaken vertical flows in convective areas by removing physically vertical correlations. It is very clear from Fig. 1 that 4DEnVar1600 outperforms 4DEnVar50 almost for all precipitation thresholds, especially for intense rain. Also for the high rain rate, compared to JNoVA, 4DEnVar1600 forecasts are worse than JNoVA forecasts for the first 12 h forecasts, which can be attributed to the fact that 4D-EnVar-NHM did not assimilate satellite radiances and surface precipitation like JNoVA. However, it is interesting to see that 4D-EnVar-NHM produces forecasts better than JNoVA for very intense rain for the next 12 h forecasts.
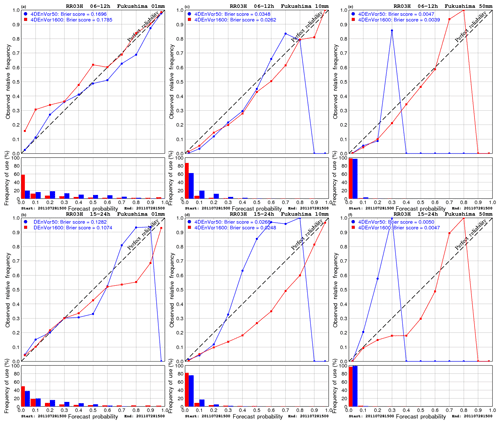
Figure 2As in Fig. 1 but for reliability diagrams of 3 h precipitation from ensemble forecasts initialized by analysis ensembles of 4D-EnVar-NHM using 1600 and 50 members. Three precipitation thresholds of 1 mm (a, b), 10 mm (c, d) and 50 mm (e, f) are chosen. Note that the ensemble forecasts were only run for the time 00:00 JST on 29 July 2011.
To check the reliability of the ensemble forecasts, reliability diagrams are calculated and plotted in Fig. 2 for 4DEnVar1600 and 4DEnVar50. Since JNoVA only provided deterministic forecasts, the reliability diagram is irrelevant for JNoVA. Note that we only performed ensemble forecasts initialized at the target time of 00:00 JST on 29 July 2001 due to lack of computational resource to run 1600-member ensemble forecasts at different initial times. Therefore, the same strategy of aggregating 3 h precipitation over the first and second 12 h forecasts in calculating the FSS in Fig. 1 is applied to obtain significant statistics. Clearly, Fig. 2 shows that 4DEnVar1600 is distinctively more reliable than 4DEnVar50 in predicting intense rain. While 4DEnVar50 cannot capture intense rain, 4DEnVar1600 tends to overestimate areas of intense rain. The tendency of overestimation of 4DEnVar1600 becomes clearer if we consider the forecast ranges between 12 and 24 h. However, for the first 12 h, 4DEnVar1600 slightly underestimates areas of light rains. This also explains why the FSSs of 4DEnVar1600 are smaller than those of 4DEnVar50 for small rainfall thresholds in Fig. 1.
As examples of the forecasts, Fig. 3 shows the accumulated precipitation at the peak period (12:00–15:00 JST on 29 July 2011) as observed and forecasted by the 4D-EnVar prediction system. Here, the rainfall observations were obtained from the operational precipitation analysis system of JMA based on radar and rain-gauge observations, which is called the radar–AMeDAS (RA) – Automated Meteorological Data Acquisition System. For comparison, the deterministic forecast initialized by the analysis from JNoVA using the same domain was also given. Note that the forecast range corresponding to this peak period is from 12 to 15 h. Clearly, the deterministic forecast initialized by 4D-EnVar-NHM outperformed that by the JNoVA, especially in terms of the location of the heavy rain, although the forecast by 4D-EnVar-NHM tended to slightly overestimate the rainfall amount, as verified by the reliability diagrams in Fig. 2. This overestimation can also be observed in the coastal area near the Sea of Japan. Note that a significant improvement was also attained against the former downscale EPS used in Part 1 (see Fig. 9 of Kobayashi et al., 2016).
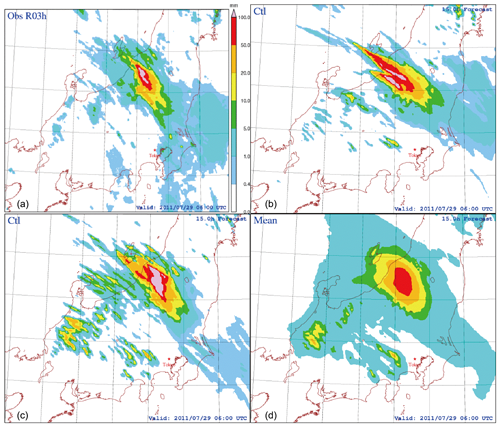
Figure 3Three-hour accumulated precipitation from 12:00 to 15:00 JST on 29 July 2011 at Niigata–Fukushima as observed by radar–AMeDAS (RA) (a), forecasted by NHM initialized by the analysis of JNoVA (b), forecasted by NHM initialized by the analysis of 4D-EnVar-NHM (c) and forecasted by the ensemble mean forecast of NHM initialized by the analysis ensemble of 4D-EnVar-NHM (d). All forecasts were started at 00:00 JST on 29 July 2011.
Since it is not possible to examine all 1600 forecasts, the ensemble mean forecast is only plotted in Fig. 3d. Again, the location of the heavy rain corresponds well with the observed location, as in the case of the deterministic forecast, but the ensemble mean precipitation is smeared out as a side effect of the averaging procedure. Therefore, the ensemble mean should not be used in our hydrological model as a representative of the ensemble forecast. Instead, all ensemble precipitation forecasts should be fed into the hydrological model to avoid rainfall distortion caused by averaging in addition to a faithful description of rainfall uncertainty. Of course with 1600 members this causes a huge increase in computational cost, and we try to reduce this burden by testing a suitable dynamical selection, described later in Sect. 4. To have a glance to the performance of the ensemble forecast we plot 1 h accumulated precipitation over the Kasahori dam catchment in time series in Fig. 4 (observed data are radar–AMeDAS). It can be seen that while the deterministic forecast could somehow reproduce the three-peak curve of the observed rainfall, ensemble members tended to capture the first peak only. Note that some members showed this three-peak curve, such as the best member, but their number was much lower than the number of ensemble members.
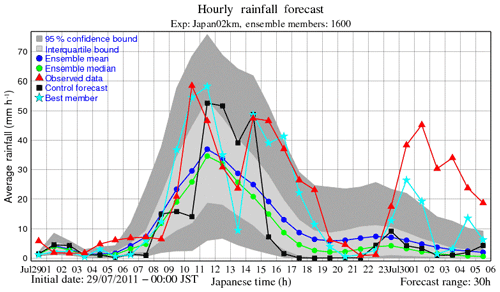
Figure 4Time series of 1 h accumulated rainfall over the catchment as forecasted by all ensemble members. The observation, control forecast, ensemble mean forecast and best member forecast are also plotted for comparison. Here, the best member is defined as the member that has the minimum distance between its time series and the observed time series.
The DRR model used in Part 1 was applied again in this paper. See Kobayashi et al. (2016) for the details. The DRR model applied was originally developed by Kojima et al. (2007) and called CDRMV3. As described in the previous section, we intentionally chose a rainfall–runoff model whose specification is close to those runoff models used by national and local governments, since the purpose is more to investigate the usefulness of 1600-member ensemble rainfalls.
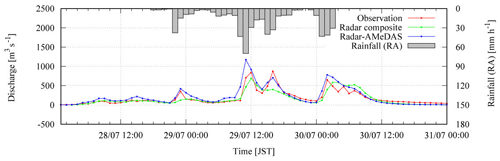
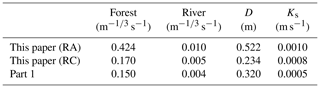
The parameters of the DRR model were recalibrated in this study using hourly radar–AMeDAS, since the amount of total rainfall for the period (762.8 mm) is closer to ground rain gauge (765.0 mm; Kobayashi et. al., 2016). The hourly radar composite (RC; radar data) of JMA was also used for another recalibration as a reference, since radar precipitation data are in general the primary source for real-time flood forecasting. The total rainfall amount with RC was 568.5 mm, which is smaller than the ground rain gauge (765.0 mm). The recalibrated equivalent roughness coefficients of the forest, the Manning coefficients of the river and the identified soil-related parameters are described in Table 1 with the parameters in Part 1. The simulated discharge hydrographs by RA and RC and observations are shown in Fig. 5 with a RA hyetograph. The duration of the calibration simulation is from 01:00 JST on 28 July to 00:00 JST on 31 July 2011.
Table 1The equivalent roughness coefficient of the forest, the Manning coefficient of the river, and identified soil-related parameters of Part 2 (this paper) and Part 1 (Kobayashi et al., 2016).
The Nash–Sutcliffe efficiency (hereinafter NSE: Nash and Sutcliffe, 1970), which is used for the assessment of model performance, is calculated as follows:
where N is the total number of time steps (1 h interval), is observed dam inflow (discharge) at time i, is simulated dam inflow (discharge) at time i, and Qm is the average of the observed dam inflows.
In the calibration simulations in Fig. 5, the NSEs with RA and RC are 0.686 and 0.743, respectively. Although the NSE with RA is worse than RC, the total rainfall amount with RA is considered more accurate, and the second and third discharge peaks seem to be captured better with RA; thus the following discussion will be made basically with the parameters calibrated with RA. Some results with RC will be added as references. The main difference of the parameters between RA and RC is that the surface soil thickness D to hold the rainfall at the initial stage is thicker in RA, which yields the lower discharge in the river.
In this section, the results of the ensemble flood simulations are shown, focusing on two aspects:
-
We examined whether the ensemble inflow simulations can show the necessity of the flood control operation and emergency operation with the probability and sufficient lead time (e.g. 12 h).
-
We also examined if we could obtain high accuracy ensemble inflow predictions several hours (1–3 h) before the occurrence, which could contribute to the decision for optimal dam operation.
Item (1) provides us with the scenario that we can prepare for any dam operations with enough lead time. Likewise, it may enable us to initiate early evacuation of the inhabitant living downstream of the dam. Item (2) is the target that has been attempted by researchers of flood forecasting. If we could forecast the inflow almost correctly several hours before the occurrence, it could help the dam administrator with the decision for actual optimal dam operations.
4.1 Probabilistic forecast
Item (1) is considered first herein. Figure 6 shows the comparisons of the hydrographs of (a) 11 discharge simulations in Part 1, (b) the same 11 members but with a positional shift in Part 1, (c) 50 discharge simulations with 4D-EnVar-NHM and parameters by RA, (d) 1600 discharge simulations with 4D-EnVar-NHM and parameters by RA, and (e) 1600 discharge simulations with 4D-EnVar-NHM and parameters by RC. Note that the duration of the 4D-EnVar-NHM ensemble weather simulation is 30 h from 00:00 JST on 29 July 2011 to 07:00 JST on 30 July 2011, but the ensemble flood simulation is carried out only for 24 h from 03:00 JST on 29 July 2011 to 03:00 JST on 30 July 2011, since we consider that JMA-NHM uses the first 3 h to adjust its dynamics. The result in Fig. 6d and e shows that, except for the third peak, the 1600-member ensemble inflows can encompass the observed discharge within the 95 % confidence bound, which was not realized in Part 1, with 11 downscale ensemble rainfalls of 2 km resolution (Fig. 6a). In other words, the extreme rainfall intensity of the event can be reproduced by the ensemble members with 1600 4D-EnVar-NHM on some level. By comparing (d) with (e), it is recognized that the 95 % confidence and interquartile bound of (d) is narrower than (e); thus the prediction with the parameters calibrated with RA, a physically more accurate rainfall, can reduce the uncertainty of the prediction probably because of the better physical meaning in the parameters. It is considered also that the ensemble mean and median values capture the overall trend of the observations on some level.
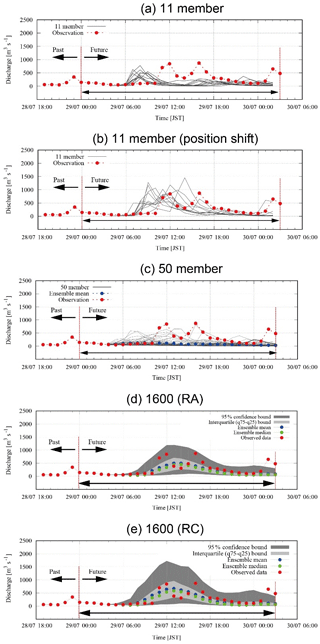
Figure 6Hydrographs of (a) 11 discharge simulations in Part 1 (Kobayashi et al., 2016), (b) the same 11 members but with a positional shift in Part 1, (c) 50 discharge simulations with 4D-EnVar-NHM and model parameters by RA, (d) 1600 discharge simulations with 4D-EnVar-NHM and model parameters by RA, and (e) 1600 discharge simulations with 4D-EnVar-NHM and model parameters by RC.
Likewise, comparing Fig. 6c and d, we can recognize that the simulated discharges by 50 ensemble rainfalls of 4D-EnVar-NHM do not encompass the observation within the range unlike the 1600 ensembles; thus 50 ensemble discharges cannot be used for the forecasting as they are.
Figure 7 shows the probability that the inflow discharge is beyond 140 m3 s−1 (hereinafter expressed as q>140, where q is the discharge), the threshold value for starting the flood control operations. The figure considers the temporal shift of the ensemble rainfalls, i.e., temporal uncertainty due to the imperfect rainfall simulation. In the figure, 0 h uncertainty means that we only considered discharges at time t to calculate probability, while the 1 h uncertainty means that we considered the discharges at t−1, t, t+1, to calculate probability, and the 2 h uncertainty means that we considered the discharges at t−2, t−1, t, t+1, t+2, to calculate probability. The 3 and 4 h uncertainties were calculated in the same way. It becomes clear from the figure that the starting time of q>140 is likely at around t = 10:00 JST on 29 July, where all curves cross, while the ending time is likely at t = 19:00 JST, where all curves cross again. Before and after the cross points there are jumps in the probabilities. In other words, the forecast can indicate that the situation of q>140 would take place after 10 h from the beginning of forecasting with the probability of around 50 %.
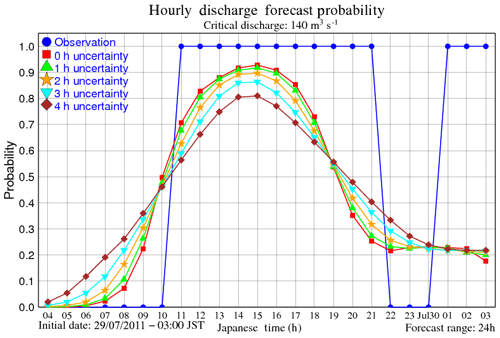
Figure 7Probability that the simulated inflow is beyond 140 m3 s−1 considering temporal uncertainty.
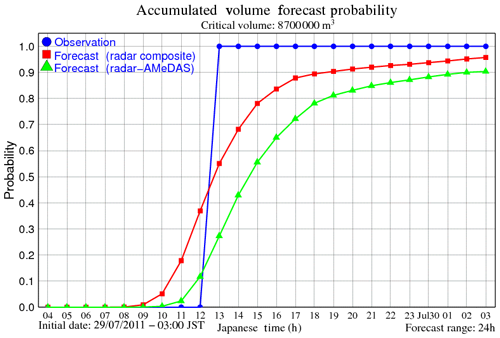
On the other hand, the emergency operation was undertaken in the actual flood event. In the emergency operation, the dam outflow has to equal the inflow to avoid dam failure as the water level approaches the top of the dam body. As written in Part 1, when the reservoir water level reaches EL 206.6 m (EL – elevation level), an emergency operation is undertaken, and the outflow is set to equal the inflow. As the height–volume (H–V) relationship of the dam reservoir was not known during the study, we judged the necessity of the emergency operation by whether the cumulative dam inflow was beyond the flood control capacity of 8 700 000 m3. Actually, the flood control capacity had not been previously filled during regular operations more than the estimation given herein, since the dam can release the dam water by natural regulation. However, again, since we do not know some of the relationships to calculate the dam water level, the judgment is made based on whether the cumulative dam inflow exceeds the flood control capacity.
Figure 8 shows the cumulative dam inflows of all the ensemble simulations starting from 03:00 JST on 29 July 2011 as well as the 95 % confidence and interquartile bound and the mean, median and observed cumulative inflow with the flood control capacity – (a) with parameters by RA and (b) with parameters by RC. Figure 8a shows that the mean of the cumulative dam inflows underestimates the observation, while in Fig. 8b the mean was roughly similar to the observation. Thus, it is considered that many of the 1600-member ensemble rainfalls still underestimate the total rainfall amount compared with RA rainfall, though the observed cumulative dam inflow is covered within the 95 % confidence interval of the ensemble inflows with RA parameters. As a reference, Fig. 8b shows that if the hydrological model parameters are calibrated with less rainfall (this case RC), underestimated ensemble rainfalls yield higher discharges, which resulted in an almost equivalent mean of the ensembles compared with the observation, though this is considered to be a bias correction from the hydrological model (see also Fig. 6d and e for the comparison). Figure 9 shows the probability that the cumulative dam inflow exceeds the flood control capacity of 8 700 000 m3. The figure indicates that, for instance, the cumulative inflow would exceed flood control capacity after 12 h from the start of the forecast with the probability of around 15 % (RA parameters) and 45 % (RC parameters). In the actual event, the cumulative inflow based on observations, and assuming no dam water release, would exceed the flood control capacity between 12:00 and 13:00 JST on 29 July 2011. Around that interval, the exceedance probability of the forecast is 15 %–30 % (RA parameters) and 35 %–55 % (RC parameters). Until around this time, the forecast shows a delay in the estimate of the cumulative dam inflow. In the end, the forecast shows that the flood control capacity will be used up with the probability of more than 90 % with regard to this flood event.
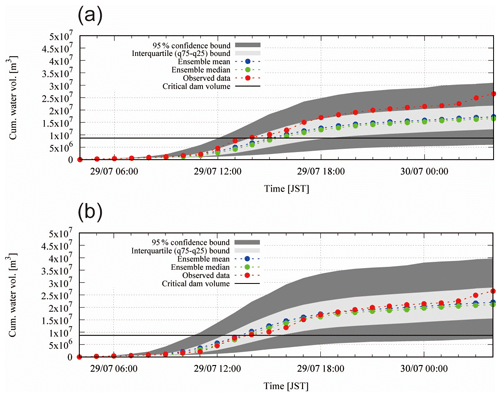
Figure 8Cumulative dam inflow by the ensemble simulations, mean of simulation and observations, and critical dam volume (a) with parameters by RA and (b) with parameters by RC.
4.2 Selection of the best members
Figure 10 shows the 95 % confidence interval of all ensemble members, the 50 best ensemble members out of 1600 ensembles selected based on NSE > 0.33 and observations. The figure shows that the selected 50 members reproduce the observations well. In some of the selected members, even the third peak is reproduced. In the case where the third peak is reproduced, the inflow hydrographs are beyond the 95 % confidence interval. Figure 11 shows the catchment average rainfalls of the 50 best ensemble inflow simulations. The black line is the observed gauge rainfall, the blue line is the radar–AMeDAS and the green line is the radar composite, while the grey lines are the 50 rainfalls for the best ensemble discharges. The rainfalls from the best 50 ensemble inflow simulations resemble those of the radar–AMeDAS.
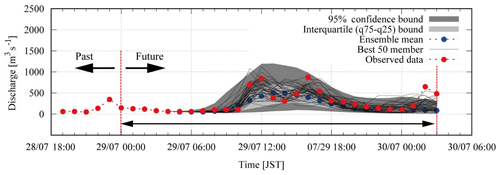
Figure 10Hydrographs of all 1600 ensemble members, the 50 best ensemble members (NSE > 0.33) and observations.
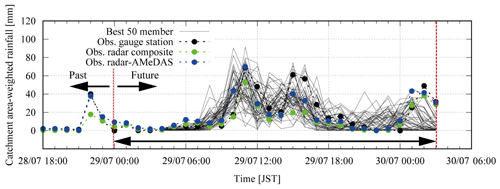
Figure 11Rainfall intensity of the 50 best ensemble inflow simulation members, of radar–AMeDAS, of radar composite and of ground observations.
Clearly, the flood forecasting becomes very useful if we could just select the best ensemble members in advance. Logically, this is impossible, since we only know the best members after knowing the observations which enable us to compute verification scores like the NSE. This raises the question of whether or not the best ensemble members can be inferred from the partial information provided by the observations in the first few hours. It is easy to see that the answer should be negative due to nonlinearity of the model and the presence of model error: the best matching in the first few hours is almost certainly not the best matching over all forecast ranges. However, it is obvious that the observations at the first few hours have a certain value which can help to reduce uncertainty in the ensemble forecast if we could incorporate this information into the forecast.
This procedure has already been well-known under the name “data assimilation”, in which we assimilate the observations at the first few hours to turn the prior probabilistic density function (pdf) given by the short-range forecasts into the posterior pdf given by the analysis ensemble (Kalnay, 2003; Reich and Cotter, 2015; Fletcher, 2017). Thus, if we know the observations at the first few hours, we should assimilate these data to replace the short-range ensemble forecasts by the ensemble analyses at these hours, then run the model initialized by the new ensemble to issue a new ensemble forecast. As a result, we should replace the definition of the best members based on verification scores by a more appropriate one based on the posterior pdf. Here, we identify the best members with the most likely members. Clearly, if we assume that the posterior pdf is unimodal, the best members should be the members clustering around the mode of this pdf, which is also the analysis. However, it is not clear how to identify the best members if this pdf is multimodal.
To overcome this problem, we will use the mathematical framework set up by particle filter (Doucet et al., 2001; Tachikawa et al., 2011). Let us denote the short-range forecasts by x1 to xK, where K is the number of ensemble members. The short-range ensemble forecast therefore yields an empirical pdf given by the sample (xi, ), with denoting the equal weight for the ith member:
Using this prior pdf as the proposal density, the posterior pdf has the following form:
Here, pY(y|xi) denotes the likelihood of the observations y conditioned on the forecast xi, and the weight is the relative likelihood. Moreover, it can be shown that pY(y|xi) is the observation evidence for the ith member (Duc and Saito, 2018). Then applying the model M as the transition model, the predictive pdf is given by
This equation shows that the contribution of each member to the predictive pdf is unequal, which differs from the prior pdf (Eq. 3). While the members with large values of dominate the predictive pdf, those with very small values of can be ignored. This suggests that the best members can be identified with the largest values of . Thus, if we sort in the descending order, the first N weights correspond to the first N best ensemble members. In this case, the predictive pdf (Eq. 5) is approximated by
Note that by introducing the notion of the best ensemble members, a substantial change occurs – that is we now work with a unequal weighted sample (xi, ). This should be taken into account in computing statistics like the ensemble mean from the best ensemble members.
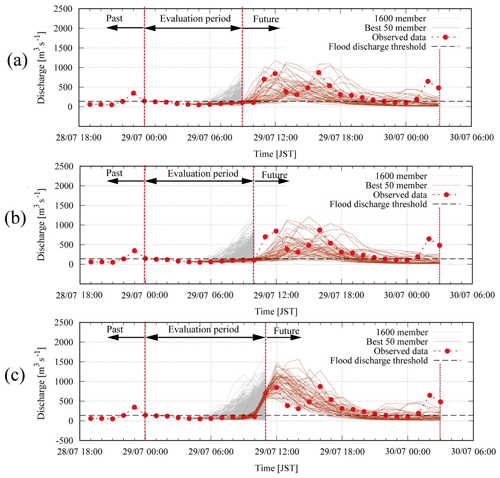
Figure 12(a) Best 50 ensemble members (NSE > 0.24) selected from first 9 h forecast, (b) best 50 ensemble members (NSE > −0.04) selected from first 10 h forecast and (c) best 50 ensemble members (NSE > 0.92) selected from first 11 h forecast.
If the likelihoods have the Gaussian form
where h is the observation operator, and R is the observation error covariance, it is easy to see that the largest weights are corresponding to the smallest weighted root-mean-square errors (WRMSEs):
Therefore, if R is a multiple of the identity matrix I, the WRMSEs become the RMSEs, which in turn are equivalent to the NSEs. This shows that selection of the best members based on verification scores over the first few hours is in fact selection of the best members based on the relative likelihoods in the posterior pdf. It can also be understood as model selection based on observation evidence (Mackay, 2003).
To check the work of this method of dynamical selection, we attempted to select some of the best members out of the 1600 members several hours in advance of the event based only on NSEs for the discharges. Figure 12a shows a result where we selected the best 50 ensemble members (NSE > 0.24) for the first 9 h from the start of the forecast. In this case, we had a 3 h lead time towards the observed peak discharge, and the selected 50 members cover the observed discharge after the first 9 h on some level. The result shows that the ensemble inflow simulations selected can indicate the possibility of rapid increases in the discharge after the first 9 h with a 3 h lead time.
Likewise Fig. 12b shows the selected best 50 members (NSE > −0.04) for the first 10 h (2 h ahead of the observed peak discharge). It is apparent that the result is worse than the previous first 9 h selection. The ensemble inflow simulations after 10 h do not cover the observation well in this case. Figure 12c shows the selected best 50 members (NSE > 0.92) for the first 11 h (1 h ahead of the observed peak discharge). In this case, the ensemble inflows after 11 h could cover the observed peak discharge 1 h later on some level, although it only has a 1 h lead time.
It is very clear from Fig. 12 that the set of the best members varies considerably with the time intervals of available observations. This is because the NSE index is sensitive to the large difference between forecasts and observations. This means that unless we simulate all the discharges of the 1600 members in advance, we may need to run many new members to update this set every time when new observations are available, and this makes management of the best members more complicated. To see why this occurs, suppose that we have a member where the sums are almost zero for the first 1, 2, …, N−1 hours when we have no rain or only light rain during this time. When we consider the next hour to reselect the best members, if the term becomes very large, this member will suddenly be out of favor despite the fact that it is always selected as one of the best members in all previous selection rounds. However, this large difference may come from spatial and temporal displacement errors of rainfall forecasts and not necessary reflect an inaccurate forecast. This shows that the use of the NSE in selecting the best members is quite sensitive to spatial and temporal displacement errors of rainfall. Part 1 of this study is an illustration for impact of spatial displacement errors on forecast performance, while Figs. 7 and 9 here show the case of temporal displacement errors. On the other hand, the NSE of rainfall cannot be used to select the best discharge members, since rainfall NSEs of similar values can produce different discharge hydrographs. For example, the catchment average rainfall with an NSE of around 0 produces discharges with an NSE close to 0.5 and −0.5. The spatial distribution of the rainfall field causes these differences even though the number of the catchment average rainfalls is the same. Even if the catchment area is small, different patterns in the rainfall field bring different discharge simulations with different NSEs. Furthermore, the error model for rainfall does not follow the Gaussian distribution, and a more appropriate distribution like a gamma or log-normal distribution should be used. However, such distributions make NSEs irrelevant, and new verification scores derived from these distributions are needed, which can take a form that is like the FSS. Thus, it is expected that if we can introduce spatial and temporal uncertainty in modeling the likelihood pY(y|xi), the predictive pdf (Eq. 6) could yield a more useful ensemble forecast. However, this requires a lengthy mathematical treatment that is worth exploring in detail in a separate study.
The study used 1600-member ensemble rainfalls produced by 4D-EnVar which contain various rainfall fields with different rainfall intensities. No post-processing such as the location correction of the rainfall field and/or rescaling of rainfall intensity was employed. The ensemble flood forecast using the 1600-member ensemble rainfalls in this study has shown that the extremely high amount of observed inflow discharge can be reproduced within the confidence interval, which was not possible by the 11-member downscale ensemble rainfalls used in Part 1. The NSE of the best member out of 1600 was 0.72. Likewise, we can calculate the probability of occurrence (e.g. the necessity of emergency dam operations) with the 1600-member ensemble rainfalls. Thus, the result of the study shows that the ensemble flood forecasting can inform us that, after 12 h for example, emergency dam operations would be required with the probability of around 15 %–30 %, the probability would be more than 90 % for the entire flood event, etc. We consider that this kind of information is very useful. For instance, a warning of dam water release can be issued to the inhabitant in the downstream with enough lead time if the result obtained in this study is further applicable to other locations and events.
On the other hand, the discharge simulations with similar NSEs until X hours produce different future forecasts after the Xth hour. In other word, we cannot select the best discharge simulation from the NSE only until X hours. Herein lies the problem that NSEs are quite sensitive to spatial and temporal displacement errors in rainfall. In principle, it is possible to introduce those errors into NSEs in a way similar to FSSs. However, it should be cautious in introducing such errors into NSEs before investigating well, although such an approach has been used recently in the meteorology community. How to incorporate them qualitatively is also a problem to be addressed. Thus, in this sense, the dynamical selection of the best rainfall field from rainfall simulations considering both spatial and temporal displacement errors is required, although this was not addressed here and remains for future work.
JMA-NHM is available under the collaborative framework between the Meteorological Research Institute (MRI) and related institutes or universities. Likewise, the DRR model is available under the collaborative framework between Kobe and Kyoto universities and related institutes or universities. The JMA’s operational analyses and forecasts can be purchased at http://www.jmbsc.or.jp/jp/online/file/f-online10200.html (last access: 11 March 2020) (JMA, 2019). Likewise, radar composite analyses and radar rain-gauge analyses can be purchased at http://www.jmbsc.or.jp/jp/online/file/f-online30100.html (last access: 11 March 2020) and http://www.jmbsc.or.jp/jp/online/file/f-online30400.html (last access: 11 March 2020), respectively (JMA, 2019). The rain-gauge data and hydrological data were provided by MLIT (personal communication, 2011), the Niigata Prefecture (personal communication, 2011) or JMA at http://www.data.jma.go.jp/gmd/risk/obsdl/index.php (last access: 11 March 2020) (JMA, 2013). We will consider making other data available upon request. Research cooperation is preferable for the data provision.
KK managed all research activity of the paper except the 1600-member ensemble meteorological simulations. Likewise, KK contributed to a large part of the paper preparation. LD managed the research work of the meteorological part, including the 1600-member ensemble meteorological simulations. LD also contributed to a large part of the paper preparation. A carried out the 1600 rainfall–runoff simulations. TO engaged in the figure preparation and data analysis. KS provided advice on the overall research activity, especially focusing on the meteorological aspects.
The authors declare that they have no conflict of interest.
Computational results were obtained using the K computer at the RIKEN Advanced Institute for Computational Science.
This work was supported by the Ministry of Education, Culture, Sports, Science and Technology as Field 3, the Strategic Programs for Innovative Research (SPIRE) and the FLAGSHIP 2020 project (Advancement of meteorological and global environmental predictions utilizing observational “Big Data”). Project IDs are as follows: hp140220, hp150214, hp160229, hp170246, hp180194 and hp190156.
This paper was edited by Kai Schröter and reviewed by Alan Seed and two anonymous referees.
Cloke, H. L. and Pappenberger, F.: Ensemble flood forecasting: A review, J. Hydrol., 375, 613–626, https://doi.org/10.1016/j.jhydrol.2009.06.005, 2009.
Doucet, A., de Freitas, N., and Gordon, N. J.: Sequential Monte Carlo Methods in Practice, Springer-Verlag, New York, USA, 2001.
Duc, L. and Saito, K.: A 4DEnVAR data assimilation system without vertical localization using the K computer, in: Japan Geoscience Union meeting, 20–25 May 2017, Chiba, Japan, AAS12-P04, 2017.
Duc, L. and Saito, K.: Verification in the presence of observation errors: Bayesian point of view, Q. J. Roy. Meteorol. Soc., 144, 1063–1090, https://doi.org/10.1002/qj.3275, 2018.
Fletcher, S. J.: Data Assimilation for the Geosciences: From Theory to Application, Elsevier, Amsterdam, the Netherlands, 2017.
Hacker, J. P., Ha, S. Y., Snyder, C., Berner, J., Eckel, F. A., Kuchera, E., Pochernich, M., Rugg, S., Schramm, J., and Wang, X.: The US Air Force Weather Agency's mesoscale ensemble: scientific description and performance results, Tellus A, 63, 625–641, https://doi.org/10.1111/j.1600-0870.2010.00497.x, 2011.
Hohenegger, C., Walser, A., Langhans, W., and Schaer, C.: Cloud-resolving ensemble simulations of the August 2005 Alpine flood, Q. J. Roy. Meteorol. Soc., 134, 889–904, https://doi.org/10.1002/qj.252, 2008.
JMA – Japan Meteorological Agency: Report on “the 2011 Niigata-Fukushima heavy rainfall event”, typhoon Talas (1112) and typhoon Roke (1115), Tech. Rep. JMA, available at: http://www.jma.go.jp/jma/kishou/books/gizyutu/134/ALL.pdf (last access: 11 March 2020), 2013.
JMA – Japan Meteorological Agency: Outline of the operational numerical weather prediction at the Japan Meteorological Agency, Tech. Rep. JMA, available at: https://www.jma.go.jp/jma/jma-eng/jma-center/nwp/outline2019-nwp/pdf/outline2019_all.pdf (last access: 11 March 2020), 2019.
Kalnay, E.: Atmospheric modeling, data assimilation and predictability, Cambridge Univ. Press, London, UK, 2003.
Kobayashi, K., Otsuka, S., Apip, and Saito, K.: Ensemble flood simulation for a small dam catchment in Japan using 10 and 2 km resolution nonhydrostatic model rainfalls, Nat. Hazards Earth Syst. Sci., 16, 1821–1839, https://doi.org/10.5194/nhess-16-1821-2016, 2016.
Kojima, T., Takara, K., and Tachikawa, Y.: A distributed runoff model for flood prediction in ungauged basin, Predictions in ungauged basins: PUB kick off, IAHS Publ., Oxfordshire, UK, 267–274, 2007.
Mackay, D. J. C.: Information theory, inference, and learning Algorithms, Cambridge Univ. Press, London, UK, 2003.
Marsigli, C., Montani, A., Nerozzi, F., Paccagnella, T., Tibaldi, S., Molteni, F., and Buizza, R.: A strategy for high–resolution ensemble prediction. Part II: limited-area experiments in four alpine flood events, Q. J. Roy. Meteorol. Soc., 127, 2095–2115, https://doi.org/10.1002/qj.49712757613, 2001.
Molteni, F., Buizza, R., Marsigli, C., Montani, A., Nerozzi, F., and Paccagnella, T.: A strategy for high-resolution ensemble prediction. I: Definition of representative members and global-model experiments, Q. J. Roy. Meteorol. Soc., 127, 2069–2094, https://doi.org/10.1002/qj.49712757612, 2001.
Montani, A., Cesari, D., Marsigli, C., and Paccagnella, T.: Seven years of activity in the field of mesoscale ensemble forecasting by the COSMO-LEPS system: main achievements and open challenges, Tellus A, 63, 605–624, https://doi.org/10.1111/j.1600-0870.2010.00499.x, 2011.
Nash, J. E. and Sutcliffe, V.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, https://doi.org/10.1016/0022-1694(70)90255-6, 1970.
Niigata Prefecture: Niigata/Fukushima extreme rainfall disaster survey documentation (as of 22 August 2011), available at: http://www.pref.niigata.lg.jp/kasenkanri/1317679266491.html (last access: 11 March 2020), 2011.
Reich, S. and Cotter, C.: Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge Univ. Press, UK, 2015.
Roberts, N. M. and Lean H. W.: Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events, Mon. Weather Rev., 136, 78–97, https://doi.org/10.1175/2007MWR2123.1, 2008.
Saito, K., Fujita, T., Yamada, Y., Ishida, J., Kumagai, Y., Aranami, K., Ohmori, S., Nagasawa, R., Kumagai, S., Muroi, C., Katao, T., Eito, H., and Yamazaki, Y.: The operational JMA nonhydrostatic meso-scale model, Mon. Weather Rev., 134, 1266–1298, https://doi.org/10.1175/MWR3120.1, 2006.
Saito, K., Origuchi, S., Duc, L., and Kobayashi, K.: Mesoscale ensemble forecast experiment of the 2011 Niigata-Fukushima heavy rainfall, Technical Report of the Japan Meteorological Agency, 170–184, available at: http://www.jma.go.jp/jma/kishou/books/gizyutu/134/ALL.pdf (last access: 12 February 2020), 2013.
Serafin, S, Strauss, L., and Dorninger, M.: Ensemble reduction using cluster analysis, Q. J. Roy. Meteorol. Soc., 145, 659–674, https://doi.org/10.1002/qj.3458, 2019.
Tachikawa, Y., Sudo, M, Shiiba, M., Yorozu, K., and Sunmin, K.: Development of a real time river stage forecasting method using a particle filter, Journal of Japan Society of Civil Engineers, Ser. B1, 67, I_511–I_516, https://doi.org/10.2208/jscejhe.67.I_511, 2011.
Vie, B., Nuissier, O., and Ducrocq, V.: Cloud-resolving ensemble simulations of Mediterranean heavy prediction events: Uncertainty on Initial conditions and lateral boundary conditions, Mon. Weather Rev., 239, 403–423, https://doi.org/10.1175/2010MWR3487.1, 2011.
Weidle, F., Wang, Y., Tian, W., and Wang, T.: Validation of strategies using clustering analysis of ECMWF EPS for initial perturbations in a limited area model ensemble prediction system, Atmos.-Ocean, 51, 284–295, https://doi.org/10.1080/07055900.2013.802217, 2013.
Xuan, Y., Cluckie, I. D., and Wang, Y.: Uncertainty analysis of hydrological ensemble forecasts in a distributed model utilizing short-range rainfall prediction, Hydrol. Earth Syst. Sci., 13, 293–303, https://doi.org/10.5194/hess-13-293-2009, 2009.
Yu, W., Nakakita, E., Kim, S., and Yamaguchi, K.: Assessment of ensemble flood forecasting with numerical weather prediction by considering spatial shift of rainfall fields, KSCE J. Civ. Eng., 22, 3686–3696, https://doi.org/10.1007/s12205-018-0407-x, 2018.